线段树 面积并问题 hdu 1255 1542

重点整理面积并的思想 以及PushUp的及时更新 还有就是cover的实现 以及建树每个节点存的信息（每个节点存的是一个线段的信息）

http://www.tuicool.com/articles/6Zf6J3 大致思想   

再就是 得注意线段树维护的信息是什么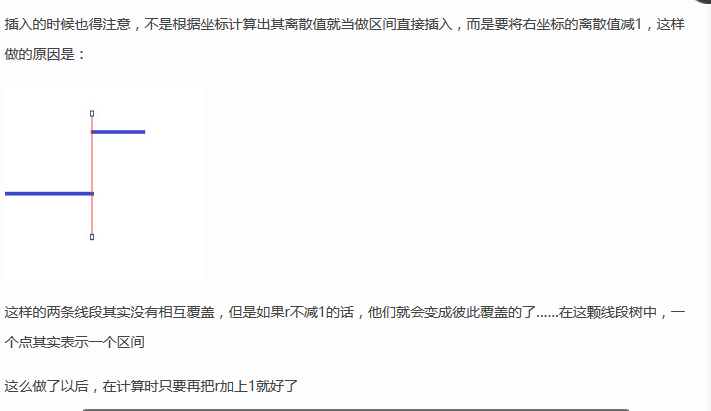

如图所示 一个点维护的是一段线段的长度

然后在对浮点数建树的时候 得用上离散化的思想

#include<cstdio>
#include<string.h>
#include<iostream>
#define maxn 10005
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#include<algorithm>
using namespace std;
struct node//区分线段树节点的值 以及线段树需要维护的值
{
    double x1,x2,y;
    int c;
    node(double x1=0,double x2=0,double y=0,int c=0):x1(x1),x2(x2),y(y),c(c){}//自定义函数 用来初始化赋值
    bool friend operator<(node a,node b) 
    {
        return a.y<b.y;
    }
};
double sum2[maxn<<2],sum1[maxn<<2];
int cover[maxn<<2];//用来表示该段完全覆盖的次数
double x[maxn<<1];
void Pushup(int rt,int l,int r)//cover表示的是一个区间完全覆盖的次数 注意 是完全覆盖！
{
    if(cover[rt]>=2) sum2[rt]=x[r]-x[l-1],sum1[rt]=x[r]-x[l-1];//当覆盖超过两次的时候 满足条件 直接计算
    else
    {
        if(cover[rt]==1)
        {
            sum1[rt]=x[r]-x[l-1];
            if(l==r) sum2[rt]=0;
            else sum2[rt]=sum1[rt<<1]+sum1[rt<<1|1];// 在确定这段已经完全覆盖的一次的时候 要看子段是否有覆盖一次的 有的话 加起来就是两次了
        } 
        else 
        if(l==r) sum2[rt]=0,sum1[rt]=0;
        else sum1[rt]=sum1[rt<<1]+sum1[rt<<1|1],sum2[rt]=sum2[rt<<1]+sum2[rt<<1|1];// 这段确定一次都没有完全覆盖的时候 看子段是否有覆盖的情况
    }
}
void build(int l,int r,int rt)
{
    cover[rt]=0;
    if(l==r)
    {
        sum1[rt]=0;
        sum2[rt]=0;
        return;
    }
    int m=(l+r)/2;
    build(lson);
    build(rson);
    Pushup(rt,l,r);
}
void updata(int l,int r,int rt,int L,int R,int c)
{
   if(L<=l&&r<=R)
   {
       cover[rt]+=c;
       Pushup(rt,l,r);
       return;
   }
   int m=(l+r)/2;
   if(L<=m) updata(lson,L,R,c);
   if(R>m)  updata(rson,L,R,c);
   Pushup(rt,l,r);
}
int main()
{
    int n,Case=1,t;
    node stu[maxn<<1];
    cin>>t;
    while(t--)
    {
        scanf("%d",&n);
        for(int i=0;i<n;i++)
        {
            double x1,y1,x2,y2;
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            stu[i*2]=node(x1,x2,y1,1);//底边为1     //扫描的时候 用来更改cover的值
            stu[i*2+1]=node(x1,x2,y2,-1);//顶边为-1 
            x[i*2]=x1,x[i*2+1]=x2;
        }
        sort(x,x+2*n);/离散化第一步 排序
        int nn=unique(x,x+2*n)-x;//第二步 去重
        build(1,nn,1);
        sort(stu,stu+2*n);//按高度递增排序
        double ans=0;

        for(int i=0;i<2*n-1;i++)
        {
            int l=lower_bound(x,x+nn,stu[i].x1)-x+1;//二分是要在去重之后的长度进行的 
            int r=lower_bound(x,x+nn,stu[i].x2)-x;
            updata(1,nn,1,l,r,stu[i].c);
            ans+=(stu[i+1].y-stu[i].y)*sum2[1]; //当 stu[i+1].y-stu[i].y 的值不为0的时候 说明一层统计结束 sum【1】表示这层总线段长度

        } printf("%.2lf
",ans); } return 0; }