题目描述:
编写一个算法来判断一个数 n 是不是快乐数。「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1。如果可以变为1,那么这个数就是快乐数。如果 n 是快乐数就返回 True ;不是,则返回 False 。
题解:
分三种情况讨论:
- 能够变为1
- 存在循环导致无法变为1
- 数字逐渐增大导致无法变为1
首先证明第三种情况是不存在的。先给出一个表如下:
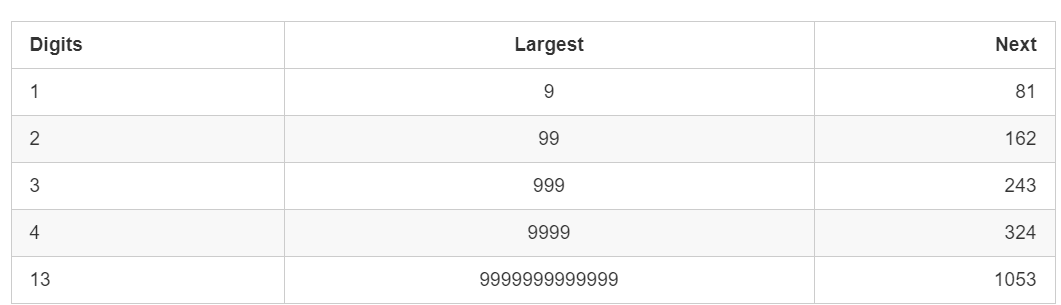
对于 33 位数的数字,它不可能大于 243243。这意味着它要么被困在 243243 以下的循环内,要么跌到 11。44 位或 44 位以上的数字在每一步都会丢失一位,直到降到 33 位为止。所以我们知道,最坏的情况下,算法可能会在 243243 以下的所有数字上循环,然后回到它已经到过的一个循环或者回到 11。但它不会无限期地进行下去,所以我们排除第三种选择。
剩下的第1、2种情况,实际上就是单链表判断是否有环的问题,每个节点的$next$通过计算当前节点每个位置上的数字平方和即可。
AC代码:
class Solution { public: // 快慢指针循环 int get_next(int x) { int tmp = 0; while(x) { tmp += (x%10)*(x%10); x/=10; } return tmp; } bool isHappy(int n) { int slow = get_next(n); int faster = get_next(get_next(n)); while(slow != faster) { faster = get_next(get_next(faster)); slow = get_next(slow); //cout << slow << endl; } if(slow == 1) return true; return false; } };