1.
GZS的三角形
发布时间: 2015年9月6日 15:18 最后更新: 2016年6月26日 12:10 时间限制: 1000ms 内存限制: 256M
机智无比的G神今天完成了一天的任务,实在是无聊的紧,拿起一支笔在纸上画起了三角形,边长为1, 2, 3,.........
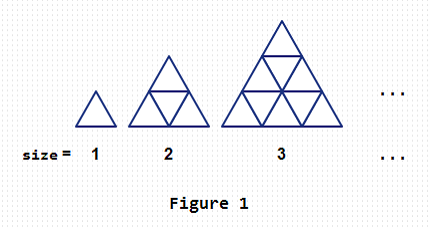
即使是无聊到这种程度,G神发达的大脑也在不停的思考,从顶部的点到沿着所画出的边到达底边的方案有多少种呢。
结果可能比较大, 结果对1000003取余。
例如,边长为2的情况如下所示:
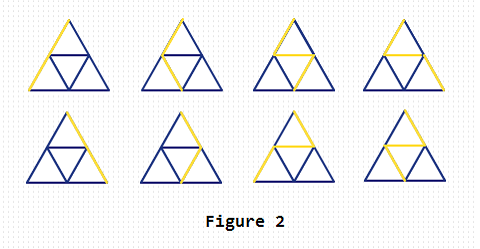
第一行有一个整数 T (1 <= T <= 1000) ,是三角形的个数。
接下来T行,每行一个整数 N (1 <= N <= 10^18),代表三角形边长。
输出T行,每行代表方案数,结果对1000003取余。
3 1 2 3
2 8 48
规律如上:可以得到第n行即边长为n的ans[n] = 2 * ans[n-1] + (n-1) * 2*ans[n-1] = 2 * n * ans[n-1]。
但是直接这么做时间会爆,当 n >= 1000003时,对 1000003取余之后都为0。
- #include <iostream>
- #include <cstdio>
- #define M 1000003
- #define LL long long
- using namespace std;
- LL ans[M+5];
- int main(){
- int t, i;
- LL n;
- ans[1] = 2;
- for(i = 2; i < M; ++i)
- ans[i] = 2*i*ans[i-1] % M;
- cin >> t;
- while(t--){
- scanf("%lld", &n);
- if(n >= M){
- printf("0 ");
- continue;
- }
- printf("%lld ", ans[n]);
- }
- return 0;
- }
2.
棋盘里的数学
发布时间: 2016年9月13日 20:39 最后更新: 2016年9月20日 12:04 时间限制: 1000ms 内存限制: 128M
lhcoder有一个n行m列的棋盘,有一颗棋子从左上角(1,1)开始移动,每次只能往右或者往下移动一格,到右下角(n,m)一共有多少移动方案?
有多组测试数据,每组测试数据中有两个整数n和m(2 <= n, m <= 1000),代表为n行m列的棋盘。
一个整数p,代表从左上角(1,1)移动到右下角(n,m)的方案数,由于方案数可能比较大,结果请对99991取模。
2 2
2
2 3
3
规律如下:当x = 1或y = 1时,该ans = 1;除此之外,(x, y)的ans = (x-1, y)的ans + (x, y-1)的ans。
- #include <iostream>
- #include <cstdio>
- #define M 99991
- #define LL long long
- using namespace std;
- LL a[1005][1005];
- LL doo(int x, int y){
- if(a[x][y] != 0) return a[x][y];
- if(x == 1 || y == 1) return a[x][y] = 1;
- else return a[x][y] = (doo(x-1, y) + doo(x, y-1)) % M;
- }
- int main(){
- int n, m;
- a[1][2] = a[2][1] = 1;
- while(~scanf("%d %d", &n, &m)){
- printf("%lld ", doo(n, m));
- }
- return 0;
- }

