列车调度
传送门:https://pintia.cn/problem-sets/994805046380707840/problems/994805063166312448
火车站的列车调度铁轨的结构如下图所示。
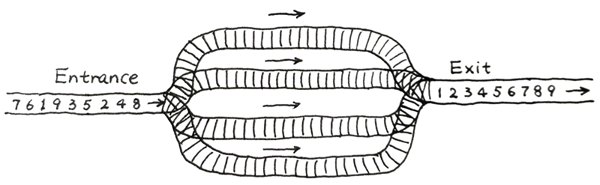
两端分别是一条入口(Entrance)轨道和一条出口(Exit)轨道,它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入,最后从出口离开。在图中有9趟列车,在入口处按照{8,4,2,5,3,9,1,6,7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开,则至少需要多少条平行铁轨用于调度?
输入格式:
输入第一行给出一个整数N (2 ≤ N ≤),下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。
输出格式:
在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。
输入样例:
9
8 4 2 5 3 9 1 6 7
输出样例:
4
题解:
第一眼:这tm看上去是单调队列啊emmm
第二眼:不对啊这是最长下降子序列。。。
考虑左边的序列右边要出来该怎么进站
很明显我们发现一个问题,在一条轨道里面,里面的数字肯定是升序排列的。。
然后我们运用我们灵活的大脑不难看出一个事实:我们尽量把一个轨道先塞满,塞不下的话再开新的轨道。。
然后你们发现这就是一题导弹拦截
也就是求有多少个最长上升子序列。。这里证明个东西,最长上升子序列的个数等于最长下降子序列的元素个数。。。
考虑我们有一个数列a1,a2,a3.....an 根据LIS的定义,每一个LIS的长度都是最长的(你读一遍中文就知道了233)
我们假设有LIS1了,那么考虑什么情况下会出现LIS2的第一位。好,那肯定是出现了一个比LIS1小的玩意。。
考虑如果我们求的不是最长的下降子序列会出现什么问题
你会发现会有部分的元素没有构成到LIS里面。或者说,他们使原先的答案变大了,因为我们要无缘无故多开几个LIS来给这些元素构成LIS。。
因为我们是考虑轨道数目最少,所以我们很自然的想到。尽量把这个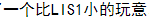
构成的序列变长。。好的我们现在问题就是求最长下降子序列。。
设F[j]表示LDS中第j位最大是多少。。
传统意义下的转移方程是f[i]=max(f[j])+1 |1<=j<i 且a[j]>a[i]
不难看出每次我们都要重新扫描一遍数据,是很累人的,所以我们运用二分查找
考虑一种贪心法则(不证明这个正确性了。。肉眼可知)
假设已知一个LDS,那么我们新进来一个数,这个数对LDS的贡献只有两种情况。。
1.这个数可以加入LDS的末尾,LDS长度+1
2.这个数不能直接加入LDS末尾,LDS长度不变
1的情况大家都很好理解,即末尾这个数比当前数大。。
2的情况我们可以考虑一件事,既然它加不进去,那么能不能更新我们的F数组吗?运用二分查找,寻找一个小于他的数,替换掉他。这样我们的问题就完美解决了。。。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define LL long long 4 const int inf =0x3f3f3f3f; 5 const int MAXN =50000+10; 6 using namespace std; 7 int arr[MAXN]; 8 int dp[MAXN]; 9 int main(){ 10 int n;cin>>n; 11 for(int i=1;i<=n;i++) scanf("%d",&arr[i]); 12 dp[1]=arr[1];//起始只有有一个数,就是arr[1] 13 int len=1;//记录了当前LIS的长度 14 for(int i=2;i<=n;i++){ 15 if(arr[i]>dp[len]) //当arr[i] 大于当前LIS的最大值的时候【也就是dp数组中最后一位 dp[len]】 16 //,肯定直接把arr[i]接到LIS【dp[len]】后面就对了,同时长度加一 17 dp[++len]=arr[i]; 18 else {//否则的话,我们可以在当前的LIS序列【dp数组】中找到第一个大于等于arr[i]的数字, 19 //将其给替换【注意这样做并不会增加长度,但是却使arr[i]之后数字更加容易的 直接接到其后面。】。 20 int pos=lower_bound(dp,dp+len,arr[i])-dp; 21 //printf("pos==%d ",pos); 22 dp[pos]=arr[i]; 23 } 24 } 25 printf("%d ",len); 26 return 0; 27 }
代码来自https://blog.csdn.net/qq_37383726/article/details/76861630 我不手打了2333 感谢这位老哥。。
