洛谷:P3391 【模板】文艺平衡树（Splay）

原题地址:https://www.luogu.org/problemnew/show/P3391

题目简述

您需要写一种数据结构（可参考题目标题），来维护一个有序数列，其中需要提供以下操作：
翻转一个区间，例如原有序序列是5 4 3 2 1，翻转区间是[2,4]的话，结果是5 2 3 4 1

---

思路

Splay是一种二叉搜索树。如果不知道的话……

百度百科对BST的介绍：

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

首先明白Splay比起线段树能多干什么：

• 可以在一个有序序列中任意数后面动态插入一串数（不能比a后面一个数还大）
• 可以删除一段区间

可能描述不是很清楚，具体看这里面给的论文链接：信息学竞赛相关优秀文章合集
或者直接看这里：运用伸展树解决数列维护问题.pdf
如果搞不懂左旋右旋是什么，可以先看信息学竞赛相关优秀文章合集里的AVL树介绍。
对于AVL树是一种为了防止树结构不够优导致深度过深时间复杂度退化，在保持二叉搜索树性质不变的前提下进行的一种变换。简单说就是把往一边沉的树弄的两边平衡些。
而在Splay中，将特定点旋转到一定位置可以进行提取区间等操作，同时各种旋转间接的使树基本平衡(是的，可以构造数据卡掉。Treap树对此表示同情)。

---

左旋（下面代码里的表达:把S往上转一次）→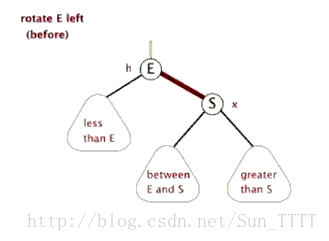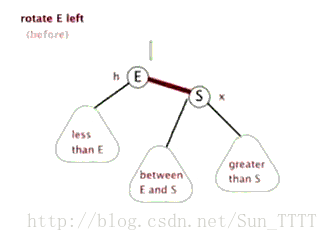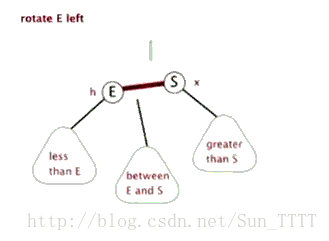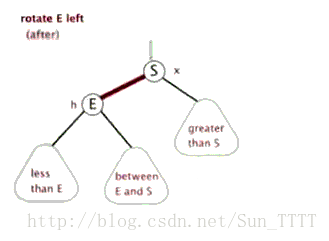

---

右旋（下面代码里的表达:把E往上转一次）→

---

图片来源：http://blog.csdn.net/sun_tttt/article/details/65445754
(文章是介绍红黑树的但是这个左旋右旋操作二叉搜索树通用)
论文里讲的很详细~
具体到这道题，引用一下zcysky在题解里给出的解释：

Splay可以用来维护序列。这样的话是把Splay当作一棵区间树。  
所谓区间树和权值树的区别，大概就是区间树每个节点代表的是一段区间（典型代表就是一般的线段树）  
权值树好理解一点，就是每个点真的代表一个点。  
至于翻转操作我们可以利用Splay的过程实现。详见代码。(Splay能维护序列反转也是它作为LCT的辅助树的条件之一)

作为模板题没什么好说的。这边文章主要记录板子用。感谢zcysky的板子。

代码

#include<bits/stdc++.h>
#define N 100005
using namespace std;
int n,m; 
int fa[N],ch[N][2],size[N],rev[N],rt;//fa[a]表示a的父亲
inline void pushup(int x)//维护节点大小
{
    size[x]=size[ch[x][0]]+size[ch[x][1]]+1;
}
void pushdown(int x)//标记下传
{
    if(rev[x]){//是否翻转了区间
        swap(ch[x][0],ch[x][1]);
        rev[ch[x][0]]^=1;rev[ch[x][1]]^=1;rev[x]=0;
    }
}
inline bool isLeft(int x) {return ch[fa[x]][0] == x;}//判断x是不是左儿子
void rotate(int x,int &k)//旋转
{
    int y=fa[x],z=fa[y];
	int kind=isLeft(x);
    if(y==k)
        k=x;
    else
        ch[z][!isLeft(y)]=x;
    ch[y][!kind]=ch[x][kind];
    
    fa[ch[y][!kind]]=y;
    ch[x][kind]=y;
    fa[y]=x;fa[x]=z;
    pushup(x);pushup(y);
}
void splay(int x,int &k)//伸展操作，将x一直旋转直到x就是k
{
    while(x!=k){
        int y=fa[x],z=fa[y];
        if(y!=k)
        	isLeft(x)^isLeft(y) ? rotate(x,k):rotate(y,k);
			//该节点与父亲分别是他们爸的左孩子\右孩子或者是右孩子\左孩子旋转2次x
			//该节点与父亲同是他们爸的左孩子或同是右孩子先旋转一次y再旋转一次x
        rotate(x,k);
    }
}
void build(int l,int r,int f) //建立一颗完全平衡的二叉树
{
    if(l>r)
        return;
    int mid=(l+r)/2;
    ch[f][!(mid<f)]=mid;
    fa[mid]=f;
    size[mid]=1;
    if(l==r)
        return;
    build(l,mid-1,mid);
    build(mid+1,r,mid);
    pushup(mid);
}
int find(int x,int k)//寻找以x为根的子树里第k大的
{
    pushdown(x);
    int s=size[ch[x][0]];
    if(k==s+1)
        return x;
    if(k<=s)
        return find(ch[x][0],k);
    else 
        return find(ch[x][1],k-s-1);
}
void rever(int l,int r)//关于如何从Splay中提取区间请看上文思路中的论文
{
    int x=find(rt,l),y=find(rt,r+2);
    splay(x,rt);
    splay(y,ch[x][1]);
    int z=ch[y][0];
    rev[z]^=1;
}
int main()
{
    scanf("%d%d",&n,&m);
    rt=(n+3)/2;
    build(1,n+2,rt);//区间左右各多加1个数方便提取区间
    for(int i=1;i<=m;i++){
        int L,R;
        scanf("%d%d",&L,&R);
        rever(L,R);
    }
    for(int i=2;i<=n+1;i++)
        printf("%d ",find(rt,i)-1);
    return 0;
}