虚树入门笔记

虚树学习笔记

前置芝士：LCA，Dfs序

参考内容 博客园“浅谈虚树”， 洛谷日报“浅谈虚树”（实际上是同一篇/lh）

虚树的定义

对于一棵给定的 (n) 个节点的树 (T)，构造新树 (T') 使其包含指定点集及它们的 LCA， 且节点数最小。这样的 (T') 被称为虚树。

虚树的应用

虚树可以解决树上对于指定点集 (S) 的询问，时间复杂度可以实现 (mathrm{O(left| S ight|log\,n + F(left|S ight|))})，其中 F 为树上解决该问题所需复杂度， 前者则为建树复杂度。

虚树的构造

进行 LCA 与 Dfs 序预处理，对于询问的点集按照 dfs 序排序，按照这样的顺序构造。

维护一个栈，储存虚树中从根到当前节点的路径。

我们考虑对于某一个将要加入虚树的新点，设其为 (u), 此时栈顶为 (st_{top})，求出它们的 LCA。

因为根据 dfs 序排过序，新点 u 不可能是 LCA， 于是进行分情况讨论：

• 1. LCA 即为 (st_{top})，可以直接将 u 压入栈中。

  2. LCA 是两点的公共祖先且不为 (st_{top}) 或 u，说明这树长这样：

  

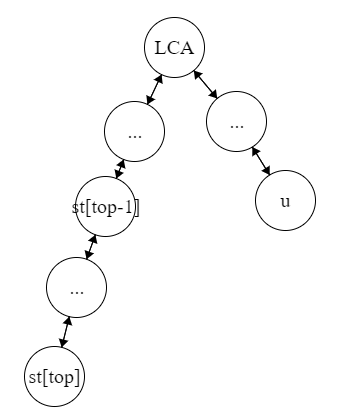
  此时我们开始弹出栈中元素并在 (st_{top}) 与 (st_{top-1}) 之间连边真正建虚树，边权用深度计算一下就好了。

  条件 (dep_{st[top - 1]} > dep_{LCA}) 时不断执行， 最后栈顶与 LCA 连边，弹出栈顶，压入 u。

执行到最后将栈中点全部弹出并连边，完成虚树构建。

建树代码 (mathbf{Code:})

inline void Inc(int x, int y) { 
    int wei = abs(dep[x] - dep[y]); 
    return e[x].push_back(mp(y, wei)), e[y].push_back(mp(x, wei)); 
}
inline void Tend(int u) { 
    if (tp == 0) return fr.push_back(st[++tp] = u); // 栈中冇点，直接压入
    int LCA = Lca(st[tp], u); 
    while (tp > 1 && dep[st[tp - 1]] > dep[LCA]) Inc(st[tp], st[tp - 1]), --tp; // 旧子树构建
   	if (dep[LCA] < dep[st[tp]]) Inc(LCA, st[tp--]);
    if (!tp || st[tp] != LCA) fr.push_back(st[++tp] = LCA);	// LCA 特殊处理
    return fr.push_back(st[++tp] = u); // 压入当前点 u
}
inline void Build(vector<int> S) {
    dep[root = 0] = 1e9, sort(S.begin(), S.end(), cmp_dfn);	// 点集按照字典序排序
    Rep(i, 0, S.size() - 1) Tend(S[i]);	//按照 DFS 序逐个压入点
    Rep(i, 0, fr.size() - 1) if (dep[fr[i]] < dep[root]) root = fr[i];	// 定根
    while (--tp > 0) Inc(st[tp], st[tp + 1]);	// 拿出最后剩下的一条链并连边
}

构造复杂度

瓶颈在于点集排序和树上 LCA ，加上了个栈，每个元素进栈一次出栈一次，具体为(mathrm{O(sum (|S| log\,|S|) + sum(|S| log\,n)+ |S|)})，常数不计。

瓶颈复杂度 (mathrm{O((sum|S|) log\,n)})。

注意每次回答完询问后的清空虚树操作一定要注意时间复杂度，memset 大多致死。

当然也要注意空间复杂度，如果开了静态数组，就要算算是否会爆空间，当然 vector 是一个好选择。虽说很多虚树的题空间都会给够。

虚树类

struct Virtualtree {
    vector<int> fr; vector<pir> e[N];
    int vs, root, top[N], si[N], dep[N], hs[N], f[N], st[N], tp;
    inline void Dfs1(int u, int fa) { hs[u] = 0, dfn[u] = ++vs, si[u] = 1, dep[u] = dep[fa] + 1, f[u] = fa; S_H(T, i, u) { int v = T.to[i]; if (v == fa) continue; Dfs1(v, u), si[u] += si[v], (si[v] >= si[hs[u]] ? hs[u] = v : 0); } }
    inline void Dfs2(int u, int k) { top[u] = k; if (!hs[u]) return void(); Dfs2(hs[u], k); S_H(T, i, u) { int v = T.to[i]; if (v == f[u] || v == hs[u]) continue; Dfs2(v, v); }}
    inline void Set(int _) { vs = tp = root = 0, fr.clear(), T.clear(); Rep(i, 0, _) e[i].clear(); Rep(i, 0, _) hs[i] = dep[i] = top[i] = st[i] = 0; }
    inline int Lca(int x, int y) { while (top[x] ^ top[y]) (dep[top[x]] < dep[top[y]] ? swap(x, y) : 0), x = f[top[x]]; return (dep[x] < dep[y] ? x : y); }
    inline void clear() { Rep(i, 0, fr.size() - 1) e[fr[i]].clear(); fr.clear(); }
    inline void Inc(int x, int y) { int wei = abs(dep[x] - dep[y]); return e[x].push_back(mp(y, wei)), e[y].push_back(mp(x, wei)); }
    inline void Chain(void) { return Dfs1(1, 0), Dfs2(1, 1); }
    inline void Tend(int u) { 
        if (tp == 0) return fr.push_back(st[++tp] = u); int LCA = Lca(st[tp], u); while (tp > 1 && dep[st[tp - 1]] > dep[LCA]) Inc(st[tp], st[tp - 1]), --tp;
        ((dep[LCA] < dep[st[tp]]) ? Inc(LCA, st[tp--]) : void()), (!tp || st[tp] != LCA ? fr.push_back(st[++tp] = LCA) : void());
        return fr.push_back(st[++tp] = u);
    }
    inline void Build(vector<int> S) {
        dep[root = 0] = 1e9, sort(S.begin(), S.end(), cmp_dfn); Rep(i, 0, S.size() - 1) Tend(S[i]);
        Rep(i, 0, fr.size() - 1) (dep[fr[i]] < dep[root]) ? root = fr[i] : 0;
        while (--tp > 0) Inc(st[tp], st[tp + 1]);
    }
} V;

建议例题

入门例题首选 CF613D Kingdom and its Cities.

再有 [SDOI2011]消耗战