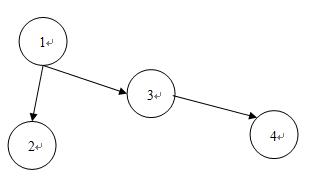
根据这道题目的意思,我们可以建一张图,对于两个booked taxi ride,ri和rj如果一辆车能够先完成ri的任务再有时间赶去完成rj的任务,那么就建立一条ri指向rj的边。
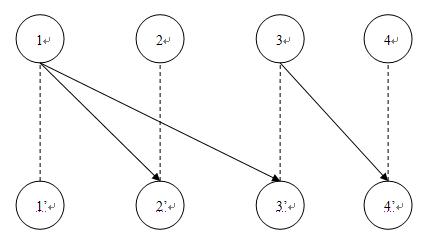
按照题目的要求,要选择最少的taxi来完成这些任务。显然在上面这个例子中,需要安排2辆taxi。结合这个图,可以把题目的要求转化为找出最少的路径条数,使得这些路径覆盖途中所有的边,例如可以选择2条路径1->3->4和1->2就可以覆盖所有的边。也可以选择1->3->4和2(因为2作为初始站,不需要由1转移过来)。对于一条连续的路径vi1->vi2->…vik由于这条路径上的任务实际上是由一辆taxi来完成的,可以吧这条路径退化成两个点vi1->vik。有了这两步建图的步骤以后,问题的求解就可以变为找出顶点集的一个最小子集,使这个顶点子集覆盖所有的边(每条边都至少和一个顶点集的顶点相连)。这个问题就是图的最小点覆盖。再看这张图,还有一些性质能够让我们更好地求出最小点覆盖。这个图是一个有向无环图,没有自环,就可以拆点,把原先建的图变成一张二分图。
可以再图中看出,上面举出的一条路径1->3->4对应了这个二分图中的路径1->3’->3->4’,在这个二分图中就需要求一个最大独立子集(这里的4点就是一条路径的终点,没一条路径即对应有一个终点!)。二分图的最大独立数是总点数与最大匹配数的差值。接下来建图,拆点,求二分图最大匹配就能解决这道题目了。
首先输入一个时间,为一辆汽车开车的时候对应的时间,然后是起点(x1,y1),再是终点(x2,y2),起点到终点的时间为|x1-x2|+|y1-y2|,假如开始的时间加上途中经历过的时间加上第一辆车得终点到第二辆车的起点的时间小于第二辆车起始的时间,那就得不要多派出一辆车
#include"stdio.h"
#include"string.h"
#include"math.h"
#define N 501
int map[N][N],v[N],link[N];
int n,m;
char time[10];
struct node
{
int x1,x2,y1,y2;
int t,sum;
}aa[N];
int fun(int x1,int y1,int x2,int y2)
{
return abs(x1-x2)+abs(y1-y2);
}
int dfs(int k)
{
int i;
for(i=0;i<m;i++)
{
if(map[k][i]&&!v[i])
{
v[i]=1;
if(link[i]==-1||dfs(link[i]))
{
link[i]=k;
return 1;
}
}
}
return 0;
}
int main()
{
int i,j,ans;
scanf("%d",&n);
while(n--)
{
scanf("%d",&m);
for(i=0;i<m;i++)
{
scanf("%s",time);
scanf("%d%d%d%d",&aa[i].x1,&aa[i].y1,&aa[i].x2,&aa[i].y2);
aa[i].t=(time[0]-'0')*60*10+(time[1]-'0')*60
+(time[3]-'0')*10+time[4]-'0';
aa[i].sum=fun(aa[i].x1,aa[i].y1,aa[i].x2,aa[i].y2);
}
memset(map,0,sizeof(map));
for(i=0;i<m-1;i++)
{
for(j=i+1;j<m;j++)
if((aa[i].t+aa[i].sum+fun(aa[i].x2,aa[i].y2,aa[j].x1,aa[j].y1))<aa[j].t)
map[i][j]=1;
}
ans=0;
memset(link,-1,sizeof(link));
for(i=0;i<m;i++)
{
memset(v,0,sizeof(v));
if(dfs(i))
ans++;
}
printf("%d\n",m-ans);
}
return 0;
}