题目大意:
一个立方体,每个点有一个值。
对于每个纵轴,都要选一个点使得选的点的总和最小且每个点与其所在纵轴相邻的纵轴的点的纵坐标之差的绝对值不能超过$d$
思路:
因为每个纵轴都只能选一个,考虑最小割
每个纵轴从S到T连一条链,对于每个限制:从一个链的点$i$向另一个链的$i-d$点连边,这样表示$x-y geq d$
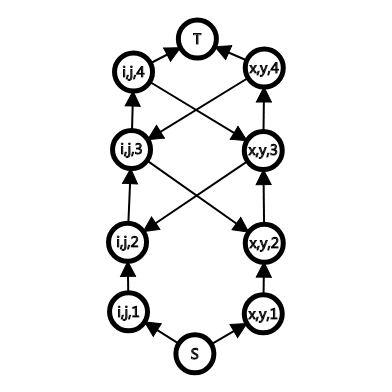
这样可以保证每一条从$S ightarrow T$的链都被割且满足条件

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 #include<map> 10 #include<set> 11 #define ll long long 12 #define db double 13 #define inf 2139062143 14 #define MAXN 65000 15 #define MAXM 290000 16 #define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i) 17 #define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i) 18 #define ren for(register int i=fst[x];i;i=nxt[i]) 19 #define Fill(x,t) memset(x,t,sizeof(x)) 20 #define pls(a,b) (a+b)%MOD 21 #define mns(a,b) (a-b+MOD)%MOD 22 #define mul(a,b) (1LL*(a)*(b))%MOD 23 using namespace std; 24 inline int read() 25 { 26 int x=0,f=1;char ch=getchar(); 27 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 28 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 29 return x*f; 30 } 31 int n,m,h,d,v[45][45][45]; 32 const int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1}; 33 struct Dinic 34 { 35 int fst[MAXN],nxt[MAXM<<1],to[MAXM<<1],cnt,val[MAXM<<1]; 36 int vis[MAXN],q[MAXN],l,r,S,T,tot,dis[MAXN],cur[MAXN]; 37 Dinic(){memset(fst,0,sizeof(fst));cnt=1,tot=0;} 38 void add(int u,int v,int w) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v,val[cnt]=w;} 39 void ins(int u,int v,int w) {add(u,v,w);add(v,u,0);} 40 int bfs() 41 { 42 vis[T]=++tot,dis[T]=0,q[l=r=1]=T;int x; 43 while(l<=r) 44 { 45 x=q[l++],cur[x]=fst[x];ren if(val[i^1]&&vis[to[i]]!=tot) 46 dis[to[i]]=dis[x]+1,vis[to[i]]=tot,q[++r]=to[i]; 47 } 48 return vis[S]==tot; 49 } 50 int dfs(int x,int a) 51 { 52 if(x==T||!a) return a;int flw=0,f; 53 for(int& i=cur[x];i&&a;i=nxt[i]) 54 if(val[i]&&dis[to[i]]==dis[x]-1&&(f=dfs(to[i],min(a,val[i])))) 55 val[i]-=f,val[i^1]+=f,a-=f,flw+=f; 56 return flw; 57 } 58 int solve(int ss,int tt,int res=0) 59 {S=ss,T=tt;while(bfs()) res+=dfs(S,inf);return res;} 60 }D; 61 int t(int x,int y,int z) {return x*n*m+y*m+z-n*m-m-1;} 62 int ok(int x,int y) {return x&&y&&x<=n&&y<=m;} 63 int main() 64 { 65 n=read(),m=read(),h=read(),d=read();int ss=n*m*h,tt=ss+1,tx,ty; 66 rep(i,1,h) rep(j,1,n) rep(k,1,m) v[i][j][k]=read(); 67 rep(j,1,n) rep(k,1,m) rep(i,1,h) 68 if(i>1) D.ins(t(i-1,j,k),t(i,j,k),v[i][j][k]);else D.ins(ss,t(i,j,k),v[i][j][k]); 69 rep(j,1,n) rep(k,1,m) rep(o,0,3) if(ok(tx=j+dx[o],ty=k+dy[o])) 70 rep(i,d+1,h) D.ins(t(i,j,k),t(i-d,tx,ty),inf); 71 rep(i,1,n) rep(j,1,m) D.ins(t(h,i,j),tt,inf); 72 printf("%d ",D.solve(ss,tt)); 73 }
