在古老的迈瑞城,巍然屹立着 $n$ 块神石。长老们商议,选取 3 块神石围成一个神坛。因为神坛的能量强度与它的面积成反比,因此神坛的面积越小越好。特殊地,如果有两块神石坐标相同,或者三块神石共线,神坛的面积为 0.000。
长老们发现这个问题没有那么简单,于是委托你编程解决这个难题。
输入格式:
输入在第一行给出一个正整数 $n$($3leq nleq 5000$)。随后 $n$ 行,每行有两个整数,分别表示神石的横坐标、纵坐标($-10^9leq 横坐标、纵坐标< 10^9$)。
输出格式:
在一行中输出神坛的最小面积,四舍五入保留 3 位小数。
输入样例:
8
3 4
2 4
1 1
4 1
0 3
3 0
1 3
4 2
输出样例:
0.500
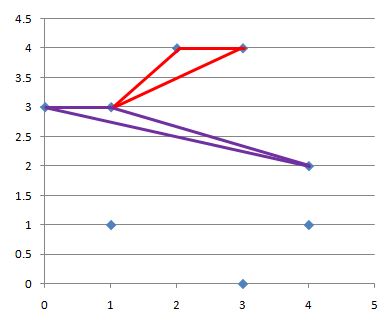
样例解释
输出的数值等于图中红色或紫色框线的三角形的面积。
传送门:
https://pintia.cn/problem-sets/994805046380707840/problems/994805046577840128
思路:
一道计算几何的题目,用极角排序来进行解答。
极角:平面上任何一点的连线和极轴的夹角,极角排序就是根据极角的大小进行排序。
假设有三点$A,B,C$(其中A为原点),则$Theta _B= frac{y_B-y_A}{x_B-x_A},Theta _C= frac{y_C-y_A}{x_C-x_A}$,
要比较$Theta _B和Theta _C$,其实就是判断$(x_C-x_A)(y_B-y_A)$和$(x_B-x_A)(y_C-y_A)$的大小。
我们枚举点$A$,来对极角进行排序。
代码:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 typedef long long ll; 6 struct point 7 { 8 ll x; 9 ll y; 10 }; 11 12 point p[5005]; 13 point e[5005]; 14 15 bool cmp(point a, point b) 16 { 17 return a.x * b.y < a.y * b.x; 18 } 19 int main() 20 21 { 22 int n; 23 scanf("%d", &n); 24 25 for(int i = 1; i <= n; i++) 26 { 27 scanf("%lld%lld", &p[i].x, &p[i].y); 28 } 29 double ans = 1e18; 30 for(int i = 1; i <= n; i++) 31 32 { 33 int cnt = 0; 34 for(int j = 1; j <= n; j++) 35 { 36 if(i != j) 37 { 38 e[cnt].x = p[i].x - p[j].x; 39 e[cnt].y = p[i].y - p[j].y; 40 cnt++; 41 } 42 } 43 44 sort(e, e + cnt, cmp); 45 for(int j = 1; j < cnt; j++) 46 ans = min(ans, 1.0 * abs(e[j].x * e[j - 1].y - e[j].y * e[j - 1].x)); 47 } 48 ans = ans / 2.0; 49 printf("%.3lf ", ans); 50 }