最小二乘法多项式拟合的Java实现

背景

由项目中需要根据一些已有数据学习出一个y=ax+b的一元二项式，给定了x,y的一些样本数据，通过梯度下降或最小二乘法做多项式拟合得到a、b，解决该问题时，首先想到的是通过spark mllib去学习，可是结果并不理想：少量的文档，参数也很难调整。于是转变了解决问题的方式：采用了最小二乘法做多项式拟合。

最小二乘法多项式拟合描述下： （以下参考：https://blog.csdn.net/funnyrand/article/details/46742561）

假设给定的数据点和其对应的函数值为 (x1, y1), (x2, y2), ... (xm, ym)，需要做的就是得到一个多项式函数f(x) = a0 * x + a1 * pow(x, 2) + .. + an * pow(x, n)，使其对所有给定x所计算出的f(x)与实际对应的y值的差的平方和最小，也就是计算多项式的各项系数 a0, a1, ... an. 

根据最小二乘法的原理，该问题可转换为求以下线性方程组的解：Ga = B，

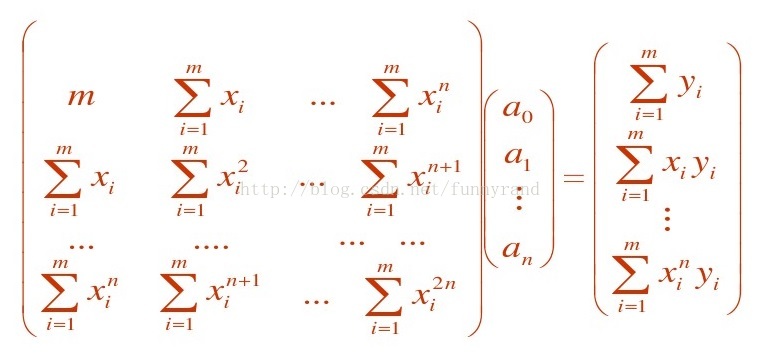
所以从编程的角度来说需要做两件事情：

1）确定线性方程组的各个系数：

确定系数比较简单，对给定的 (x1, y1), (x2, y2), ... (xm, ym) 做相应的计算即可，相关代码：

private void compute() {
　　...
}

2）解线性方程组：

解线性方程组稍微复杂，这里用到了高斯消元法，基本思想是通过递归做矩阵转换，逐渐减少求解的多项式系数的个数，相关代码：

private double[] calcLinearEquation(double[][] a, double[] b) {
　　...
}

Java代码

public class JavaLeastSquare {
    private double[] x;
    private double[] y;
    private double[] weight;
    private int n;
    private double[] coefficient;

    /**
     * Constructor method.
     * @param x Array of x
     * @param y Array of y
     * @param n The order of polynomial
     */
    public JavaLeastSquare(double[] x, double[] y, int n) {
        if (x == null || y == null || x.length < 2 || x.length != y.length
                || n < 2) {
            throw new IllegalArgumentException(
                    "IllegalArgumentException occurred.");
        }
        this.x = x;
        this.y = y;
        this.n = n;
        weight = new double[x.length];
        for (int i = 0; i < x.length; i++) {
            weight[i] = 1;
        }
        compute();
    }

    /**
     * Constructor method.
     * @param x      Array of x
     * @param y      Array of y
     * @param weight Array of weight
     * @param n      The order of polynomial
     */
    public JavaLeastSquare(double[] x, double[] y, double[] weight, int n) {
        if (x == null || y == null || weight == null || x.length < 2
                || x.length != y.length || x.length != weight.length || n < 2) {
            throw new IllegalArgumentException(
                    "IllegalArgumentException occurred.");
        }
        this.x = x;
        this.y = y;
        this.n = n;
        this.weight = weight;
        compute();
    }

    /**
     * Get coefficient of polynomial.
     * @return coefficient of polynomial
     */
    public double[] getCoefficient() {
        return coefficient;
    }

    /**
     * Used to calculate value by given x.
     * @param x x
     * @return y
     */
    public double fit(double x) {
        if (coefficient == null) {
            return 0;
        }
        double sum = 0;
        for (int i = 0; i < coefficient.length; i++) {
            sum += Math.pow(x, i) * coefficient[i];
        }
        return sum;
    }

    /**
     * Use Newton's method to solve equation.
     * @param y y
     * @return x
     */
    public double solve(double y) {
        return solve(y, 1.0d);
    }

    /**
     * Use Newton's method to solve equation.
     * @param y      y
     * @param startX The start point of x
     * @return x
     */
    public double solve(double y, double startX) {
        final double EPS = 0.0000001d;
        if (coefficient == null) {
            return 0;
        }
        double x1 = 0.0d;
        double x2 = startX;
        do {
            x1 = x2;
            x2 = x1 - (fit(x1) - y) / calcReciprocal(x1);
        } while (Math.abs((x1 - x2)) > EPS);
        return x2;
    }

    /*
     * Calculate the reciprocal of x.
     * @param x x
     * @return the reciprocal of x
     */
    private double calcReciprocal(double x) {
        if (coefficient == null) {
            return 0;
        }
        double sum = 0;
        for (int i = 1; i < coefficient.length; i++) {
            sum += i * Math.pow(x, i - 1) * coefficient[i];
        }
        return sum;
    }

    /*
     * This method is used to calculate each elements of augmented matrix.
     */
    private void compute() {
        if (x == null || y == null || x.length <= 1 || x.length != y.length
                || x.length < n || n < 2) {
            return;
        }
        double[] s = new double[(n - 1) * 2 + 1];
        for (int i = 0; i < s.length; i++) {
            for (int j = 0; j < x.length; j++) {
                s[i] += Math.pow(x[j], i) * weight[j];
            }
        }
        double[] b = new double[n];
        for (int i = 0; i < b.length; i++) {
            for (int j = 0; j < x.length; j++) {
                b[i] += Math.pow(x[j], i) * y[j] * weight[j];
            }
        }
        double[][] a = new double[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                a[i][j] = s[i + j];
            }
        }

        // Now we need to calculate each coefficients of augmented matrix
        coefficient = calcLinearEquation(a, b);
    }

    /*
     * Calculate linear equation.
     * The matrix equation is like this: Ax=B
     * @param a two-dimensional array
     * @param b one-dimensional array
     * @return x, one-dimensional array
     */
    private double[] calcLinearEquation(double[][] a, double[] b) {
        if (a == null || b == null || a.length == 0 || a.length != b.length) {
            return null;
        }

        for (double[] x : a) {
            if (x == null || x.length != a.length)
                return null;
        }

        int len = a.length - 1;
        double[] result = new double[a.length];

        if (len == 0) {
            result[0] = b[0] / a[0][0];
            return result;
        }

        double[][] aa = new double[len][len];
        double[] bb = new double[len];
        int posx = -1, posy = -1;
        for (int i = 0; i <= len; i++) {
            for (int j = 0; j <= len; j++)
                if (a[i][j] != 0.0d) {
                    posy = j;
                    break;
                }
            if (posy != -1) {
                posx = i;
                break;
            }
        }
        if (posx == -1) {
            return null;
        }

        int count = 0;
        for (int i = 0; i <= len; i++) {
            if (i == posx) {
                continue;
            }
            bb[count] = b[i] * a[posx][posy] - b[posx] * a[i][posy];
            int count2 = 0;
            for (int j = 0; j <= len; j++) {
                if (j == posy) {
                    continue;
                }
                aa[count][count2] = a[i][j] * a[posx][posy] - a[posx][j] * a[i][posy];
                count2++;
            }
            count++;
        }

        // Calculate sub linear equation
        double[] result2 = calcLinearEquation(aa, bb);

        // After sub linear calculation, calculate the current coefficient
        double sum = b[posx];
        count = 0;
        for (int i = 0; i <= len; i++) {
            if (i == posy) {
                continue;
            }
            sum -= a[posx][i] * result2[count];
            result[i] = result2[count];
            count++;
        }
        result[posy] = sum / a[posx][posy];
        return result;
    }

    public static void main(String[] args) {
        JavaLeastSquare eastSquareMethod = new JavaLeastSquare(
                new double[]{
                        2, 14, 20, 25, 26, 34,
                        47, 87, 165, 265, 365, 465,
                        565, 665
                },
                new double[]{
                        0.7 * 2 + 20 + 0.4,
                        0.7 * 14 + 20 + 0.5,
                        0.7 * 20 + 20 + 3.4,
                        0.7 * 25 + 20 + 5.8,
                        0.7 * 26 + 20 + 8.27,
                        0.7 * 34 + 20 + 0.4,

                        0.7 * 47 + 20 + 0.1,
                        0.7 * 87 + 20,
                        0.7 * 165 + 20,
                        0.7 * 265 + 20,
                        0.7 * 365 + 20,
                        0.7 * 465 + 20,

                        0.7 * 565 + 20,
                        0.7 * 665 + 20
                },
                2);

        double[] coefficients = eastSquareMethod.getCoefficient();
        for (double c : coefficients) {
            System.out.println(c);
        }

        // 测试
        System.out.println(eastSquareMethod.fit(4));
    }
}

输出结果：

com.datangmobile.biz.leastsquare.JavaLeastSquare
22.27966881467629
0.6952475907448203
25.06065917765557

Process finished with exit code 0

使用开源库

也可使用Apache开源库commons math（http://commons.apache.org/proper/commons-math/userguide/fitting.html），提供的功能更强大：

<dependency>  
    <groupId>org.apache.commons</groupId>  
    <artifactId>commons-math3</artifactId>  
    <version>3.5</version>  
</dependency>  

实现代码：

import org.apache.commons.math3.fitting.PolynomialCurveFitter;
import org.apache.commons.math3.fitting.WeightedObservedPoints;

public class WeightedObservedPointsTest {
    public static void main(String[] args) {
        final WeightedObservedPoints obs = new WeightedObservedPoints();
        obs.add(2,  0.7 * 2 + 20 + 0.4);
        obs.add(12,  0.7 * 12 + 20 + 0.3);
        obs.add(32,  0.7 * 32 + 20 + 3.4);
        obs.add(34 ,  0.7 * 34 + 20 + 5.8);
        obs.add(58 , 0.7 * 58 + 20 + 8.4);
        obs.add(43 , 0.7 * 43 + 20 + 0.28);
        obs.add(27 , 0.7 * 27 + 20 + 0.4);

        // Instantiate a two-degree polynomial fitter.
        final PolynomialCurveFitter fitter = PolynomialCurveFitter.create(2);

        // Retrieve fitted parameters (coefficients of the polynomial function).
        final double[] coeff = fitter.fit(obs.toList());
        for (double c : coeff) {
            System.out.println(c);
        }
    }
}

测试输出结果：

20.47425047847121
0.6749744063035112
0.002523043547711147

Process finished with exit code 0

使用org.ujmp(矩阵)实现最小二乘法：

pom.xml中需要引入org.ujmp

<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
    xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
    <modelVersion>4.0.0</modelVersion>
    <groupId>com.dtgroup</groupId>
    <artifactId>dtgroup</artifactId>
    <version>0.0.1-SNAPSHOT</version>

    <repositories>
        <repository>
            <id>limaven</id>
            <name>aliyun maven</name>
            <url>http://maven.aliyun.com/nexus/content/groups/public/</url>
            <layout>default</layout>
            <releases>
                <enabled>true</enabled>
            </releases>
            <snapshots>
                <enabled>false</enabled>
            </snapshots>
        </repository>
    </repositories>
    <dependencies>
        <dependency>
            <groupId>org.ujmp</groupId>
            <artifactId>ujmp-core</artifactId>
            <version>0.3.0</version>
        </dependency>
    </dependencies>
</project>

java代码：

    /**
     * 采用最小二乘法多项式拟合方式，获取多项式的系数。
     * @param sampleCount 采样点个数
     * @param fetureCount 多项式的系数
     * @param samples 采样点集合
     * **/
    private static void leastsequare(int sampleCount, int fetureCout, List<Sample> samples) {
        // 构件 2*2矩阵 存储X，元素值都为1.0000的矩阵
        Matrix matrixX = DenseMatrix.Factory.ones(sampleCount, fetureCout);

        for (int i = 0; i < samples.size(); i++) {
            matrixX.setAsDouble(samples.get(i).getX(), i, 1);
        }

        // System.out.println(matrixX);
        System.out.println("--------------------------------------");
        // 构件 2*2矩阵 存储X
        Matrix matrixY = DenseMatrix.Factory.ones(sampleCount, 1);

        for (int i = 0; i < samples.size(); i++) {
            matrixY.setAsDouble(samples.get(i).getY(), i, 0);
        }
        // System.out.println(matrixY);

        // 对X进行转置
        Matrix matrixXTrans = matrixX.transpose();
        // System.out.println(matrixXTrans);

        // 乘积运算：x*转转置后x:matrixXTrans*matrixX
        Matrix matrixMtimes = matrixXTrans.mtimes(matrixX);
        System.out.println(matrixMtimes);

        System.out.println("--------------------------------------");
        // 求逆
        Matrix matrixMtimesInv = matrixMtimes.inv();
        System.out.println(matrixMtimesInv);

        // x转置后结果*求逆结果
        System.out.println("--------------------------------------");
        Matrix matrixMtimesInvMtimes = matrixMtimesInv.mtimes(matrixXTrans);
        System.out.println(matrixMtimesInvMtimes);

        System.out.println("--------------------------------------");
        Matrix theta = matrixMtimesInvMtimes.mtimes(matrixY);
        System.out.println(theta);
    }

测试代码：

    public static void main(String[] args) {
        /**
         * y=ax+b
         * 
         * a(0,1] b[5,20]
         * 
         * x[0,500] y>=5
         */

        // y= 0.8d*x+15
        // 当x不变动时，y对应有多个值；此时把y求均值。
        List<Sample> samples = new ArrayList<Sample>();
        samples.add(new Sample(0.8d * 1 + 15 + 1, 1d));
        samples.add(new Sample(0.8d * 4 + 15 + 0.8, 4d));
        samples.add(new Sample(0.8d * 3 + 15 + 0.7, 3d));
        samples.add(new Sample(0.8d * 24 + 15 + 0.4, 24d));
        samples.add(new Sample(0.8d * 5 + 15 + 0.3, 5d));
        samples.add(new Sample(0.8d * 10 + 15 + 0.4, 10d));
        samples.add(new Sample(0.8d * 14 + 15 + 0.2, 14d));
        samples.add(new Sample(0.8d * 7 + 15 + 0.3, 7d));
        samples.add(new Sample(0.8d * 1000 + 23 + 0.3, 70d));

        int sampleCount = samples.size();
        int fetureCout = 2;

        leastsequare(sampleCount, fetureCout, samples);
    }

过滤样本中的噪点：

    public static void main(String[] args) {
        /**
         * y=ax+b
         * 
         * a(0,1] b[5,20]
         * 
         * x[0,500] y>=5
         */

        // y= 0.8d*x+15
        // 当x不变动时，y对应有多个值；此时把y求均值。
        List<Sample> samples = new ArrayList<Sample>();
        samples.add(new Sample(0.8d * 1 + 15 + 1, 1d));
        samples.add(new Sample(0.8d * 4 + 15 + 0.8, 4d));
        samples.add(new Sample(0.8d * 3 + 15 + 0.7, 3d));
        samples.add(new Sample(0.8d * 24 + 15 + 0.4, 24d));
        samples.add(new Sample(0.8d * 5 + 15 + 0.3, 5d));
        samples.add(new Sample(0.8d * 10 + 15 + 0.4, 10d));
        samples.add(new Sample(0.8d * 14 + 15 + 0.2, 14d));
        samples.add(new Sample(0.8d * 7 + 15 + 0.3, 7d));
        samples.add(new Sample(0.8d * 1000 + 23 + 0.3, 70d));

        // samples = filterSample(samples);
        sortSample(samples);
        FilterSampleByGradientResult result = filterSampleByGradient(0, samples);

        while (result.isComplete() == false) {
            List<Sample> newSamples=result.getSamples(); 
            sortSample(newSamples);
            result = filterSampleByGradient(result.getIndex(), newSamples);
        }
        samples = result.getSamples();

        for (Sample sample : samples) {
            System.out.println(sample);
        }

        int sampleCount = samples.size();
        int fetureCout = 2;

        leastsequare(sampleCount, fetureCout, samples);
    }

    /**
     * 对采样点进行排序，按照x排序，升序排列
     * @param samples 采样点集合
     * **/
    private static void sortSample(List<Sample> samples) {
        samples.sort(new Comparator<Sample>() {
            public int compare(Sample o1, Sample o2) {
                if (o1.getX() > o2.getX()) {
                    return 1;
                } else if (o1.getX() <= o2.getX()) {
                    return -1;
                }
                return 0;
            }
        });
    }

    /**
     * 过滤采样点中的噪点（采样过滤方式：double theta=(y2-y1)/(x2-x1)，theta就是一个斜率，根据该值范围来过滤。）
     * @param index 记录上次过滤索引
     * @param samples 采样点集合（将从其中过滤掉噪点）
     * **/
    private static FilterSampleByGradientResult filterSampleByGradient(int index, List<Sample> samples) {
        int sampleSize = samples.size();
        for (int i = index; i < sampleSize - 1; i++) {
            double delta_x = samples.get(i).getX() - samples.get(i + 1).getX();
            double delta_y = samples.get(i).getY() - samples.get(i + 1).getY();
            // 距离小于2米
            if (Math.abs(delta_x) < 1) {
                double newY = (samples.get(i).getY() + samples.get(i + 1).getY()) / 2;
                double newX = samples.get(i).getX();

                samples.remove(i);
                samples.remove(i + 1);
                samples.add(new Sample(newY, newX));

                return new FilterSampleByGradientResult(false, i, samples);
            } else {
                double gradient = delta_y / delta_x;
                if (gradient > 1.5) {
                    if (i == 0) {
                        // double newY = (samples.get(i).getY() + samples.get(i
                        // + 1).getY()) / 2;
                        // double newX = (samples.get(i).getX() + samples.get(i
                        // + 1).getX()) / 2;

                        // samples.remove(i);
                        // samples.add(new Sample(newY, newX));
                    } else {
                        samples.remove(i + 1);
                    }

                    return new FilterSampleByGradientResult(false, i, samples);
                }
            }
        }

        return new FilterSampleByGradientResult(true, 0, samples);
    }

 使用距离来处理过滤：

    private static List<Sample> filterSample(List<Sample> samples) {
        // x={x1,x2,x3...xn}
        // u=E(x) ---x的期望（均值）为 u
        // 6=sqrt(pow((x1-u),2)+pow((x2-u),2)+pow((x3-u),2)+...+pow((xn-u),2))
        // 6为x的标准差，标准差=sqrt(方差)
        // 剔除噪点可以采用：
        // 若xi不属于(u-3*6,u+3*6),则认为它是噪点。

        // 另外一种方案，对x/y都做上边的处理，之后如果两个结果为and 或者 or操作来选取是否剔除。
        // 用点的方式来过滤数据，求出一个中值点，求其他点到该点的距离。
        int sampleCount = samples.size();
        double sumX = 0d;
        double sumY = 0d;

        for (Sample sample : samples) {
            sumX += sample.getX();
            sumY += sample.getY();
        }

        // 求中心点
        double centerX = (sumX / sampleCount);
        double centerY = (sumY / sampleCount);

        List<Double> distanItems = new ArrayList<Double>();
        // 计算出所有点距离该中心点的距离
        for (int i = 0; i < samples.size(); i++) {
            Sample sample = samples.get(i);
            Double xyPow2 = Math.pow(sample.getX() - centerX, 2) + Math.pow(sample.getY() - centerY, 2);
            distanItems.add(Math.sqrt(xyPow2));
        }

        // 以下对根据距离（所有点距离中心点的距离）进行筛选
        double sumDistan = 0d;
        double distanceU = 0d;
        for (Double distance : distanItems) {
            sumDistan += distance;
        }
        distanceU = sumDistan / sampleCount;

        double deltaPowSum = 0d;
        double distanceTheta = 0d;
        // sqrt(pow((x1-u),2)+pow((x2-u),2)+pow((x3-u),2)+...+pow((xn-u),2))
        for (Double distance : distanItems) {
            deltaPowSum += Math.pow((distance - distanceU), 2);
        }
        distanceTheta = Math.sqrt(deltaPowSum);

        // 剔除噪点可以采用：
        // 若xi不属于(u-3*6,u+3*6),则认为它是噪点。
        double minDistance = distanceU - 0.5 * distanceTheta;
        double maxDistance = distanceU + 0.5 * distanceTheta;
        List<Integer> willbeRemoveIdxs = new ArrayList<Integer>();
        for (int i = distanItems.size() - 1; i >= 0; i--) {
            Double distance = distanItems.get(i);
            if (distance <= minDistance || distance >= maxDistance) {
                willbeRemoveIdxs.add(i);
                System.out.println("will be remove " + i);
            }
        }

        for (int willbeRemoveIdx : willbeRemoveIdxs) {
            samples.remove(willbeRemoveIdx);
        }

        return samples;
    }

实际业务测试：

package com.zjanalyse.spark.maths;

import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;

import org.ujmp.core.DenseMatrix;
import org.ujmp.core.Matrix;

public class LastSquare {
    /**
     * y=ax+b a(0,1] b[5,20] x[0,500] y>=5
     */
    public static void main(String[] args) {
        // y= 0.8d*x+15
        // 当x不变动时，y对应有多个值；此时把y求均值。
        List<Sample> samples = new ArrayList<Sample>();
        samples.add(new Sample(0.8d * 11 + 15 + 1, 11d));
        samples.add(new Sample(0.8d * 24 + 15 + 0.8, 24d));
        samples.add(new Sample(0.8d * 33 + 15 + 0.7, 33d));
        samples.add(new Sample(0.8d * 24 + 15 + 0.4, 24d));
        samples.add(new Sample(0.8d * 47 + 15 + 0.3, 47d));
        samples.add(new Sample(0.8d * 60 + 15 + 0.4, 60d));
        samples.add(new Sample(0.8d * 14 + 15 + 0.2, 14d));
        samples.add(new Sample(0.8d * 57 + 15 + 0.3, 57d));
        samples.add(new Sample(0.8d * 70 + 60 + 0.3, 70d));
        samples.add(new Sample(0.8d * 80 + 60 + 0.3, 80d));
        samples.add(new Sample(0.8d * 40 + 30 + 0.3, 40d));

        sortSample(samples);
        System.out.println("原始样本数据");
        for (Sample sample : samples) {
            System.out.println(sample);
        }

        System.out.println("开始“所有点”通过“业务数据取值范围”剔除：");
        // 按照业务过滤。。。
        filterByBusiness(samples);
        System.out.println("结束“所有点”通过“业务数据取值范围”剔除：");

        for (Sample sample : samples) {
            System.out.println(sample);
        }

        int sampleCount = samples.size();
        int fetureCout = 2;
        System.out.println("第一次拟合。。。");
        Matrix theta = leastsequare(sampleCount, fetureCout, samples);

        double wear_loss = theta.getAsDouble(0, 0);
        double path_loss = theta.getAsDouble(1, 0);

        System.out.println("wear loss " + wear_loss);
        System.out.println("path loss " + path_loss);

        System.out.println("开始“所有点”与“第一多项式拟合结果直线方式距离方差”剔除：");
        samples = filterSample(wear_loss, path_loss, samples);
        System.out.println("结束“所有点”与“第一多项式拟合结果直线方式距离方差”剔除：");

        for (Sample sample : samples) {
            System.out.println(sample);
        }

        System.out.println("第二次拟合。。。");
        sampleCount = samples.size();
        fetureCout = 2;

        if (sampleCount >= 2) {
            theta = leastsequare(sampleCount, fetureCout, samples);

            wear_loss = theta.getAsDouble(0, 0);
            path_loss = theta.getAsDouble(1, 0);

            System.out.println("wear loss " + wear_loss);
            System.out.println("path loss " + path_loss);
        }
        System.out.println("complete...");
    }

    /**
     * 按照业务过滤有效值范围
     */
    private static void filterByBusiness(List<Sample> samples) {
        for (int i = 0; i < samples.size(); i++) {
            double x = samples.get(i).getX();
            double y = samples.get(i).getY();
            if (x >= 500) {
                System.out.println(x + " x值超出有效值范围[0,500)");
                samples.remove(i);
                i--;
            }
            // y= 0.8d*x+15
            else if (y < 0 * x + 5 || y > 1 * x + 30) {
                System.out.println(
                        y + " y值超出有效值范围[(0*x+5),(1*x+30)]其中x=" + x + ",也就是：[" + (0 * x + 5) + "," + (1 * x + 30) + ")");
                samples.remove(i);
                i--;
            }
        }
    }

    /**
     * Description 点到直线的距离
     * 
     * @param x1
     *            点横坐标
     * @param y1
     *            点纵坐标
     * @param A
     *            直线方程一般式系数A
     * @param B
     *            直线方程一般式系数B
     * @param C
     *            直线方程一般式系数C
     * @return 点到之间的距离
     * @see 点0,1到之前y=x+0的距离 <br>
     *      double distance = getDistanceOfPerpendicular(0,0, -1, 1, 0);<br>
     *      System.out.println(distance);<br>
     */
    private static double getDistanceOfPerpendicular(double x1, double y1, double A, double B, double C) {
        double distance = Math.abs((A * x1 + B * y1 + C) / Math.sqrt(A * A + B * B));
        return distance;
    }

    private static List<Sample> filterSample(double wear_loss, double path_loss, List<Sample> samples) {
        // x={x1,x2,x3...xn}
        // u=E(x) ---x的期望（均值）为 u
        // 6=sqrt(pow((x1-u),2)+pow((x2-u),2)+pow((x3-u),2)+...+pow((xn-u),2))
        // 6为x的标准差，标准差=sqrt(方差)
        // 剔除噪点可以采用：
        // 若xi不属于(u-3*6,u+3*6),则认为它是噪点。

        // 求出所有点距离第一次拟合结果的直线方程的距离
        int sampleCount = samples.size();
        List<Double> distanItems = new ArrayList<Double>();
        // 计算出所有点距离该中心点的距离
        for (int i = 0; i < samples.size(); i++) {
            Sample sample = samples.get(i);
            double distance = getDistanceOfPerpendicular(sample.getX(), sample.getY(), path_loss, -1, wear_loss);
            distanItems.add(Math.sqrt(distance));
        }

        // 以下对根据距离（所有点距离中心点的距离）进行筛选
        double sumDistan = 0d;
        double distanceU = 0d;
        for (Double distance : distanItems) {
            sumDistan += distance;
        }
        distanceU = sumDistan / sampleCount;

        double deltaPowSum = 0d;
        double distanceTheta = 0d;
        // sqrt(pow((x1-u),2)+pow((x2-u),2)+pow((x3-u),2)+...+pow((xn-u),2))
        for (Double distance : distanItems) {
            deltaPowSum += Math.pow((distance - distanceU), 2);
        }
        distanceTheta = Math.sqrt(deltaPowSum);

        // 剔除噪点可以采用：
        // 若xi不属于(u-3*6,u+3*6),则认为它是噪点。
        double minDistance = distanceU - 0.25 * distanceTheta;
        double maxDistance = distanceU + 0.25 * distanceTheta;
        List<Integer> willbeRemoveIdxs = new ArrayList<Integer>();

        for (int i = distanItems.size() - 1; i >= 0; i--) {
            Double distance = distanItems.get(i);
            if (distance <= minDistance || distance >= maxDistance) {
                System.out.println(distance + " out of range [" + minDistance + "," + maxDistance + "]");
                willbeRemoveIdxs.add(i);
            } else {
                System.out.println(distance);
            }
        }

        for (int willbeRemoveIdx : willbeRemoveIdxs) {
            Sample sample = samples.get(willbeRemoveIdx);
            System.out.println("remove " + sample);
            samples.remove(willbeRemoveIdx);
        }

        return samples;
    }

    /**
     * 对采样点进行排序，按照x排序，升序排列
     * 
     * @param samples
     *            采样点集合
     **/
    private static void sortSample(List<Sample> samples) {
        samples.sort(new Comparator<Sample>() {
            public int compare(Sample o1, Sample o2) {
                if (o1.getX() > o2.getX()) {
                    return 1;
                } else if (o1.getX() <= o2.getX()) {
                    return -1;
                }
                return 0;
            }
        });
    }

    /**
     * Description 采用最小二乘法多项式拟合方式，获取多项式的系数。
     * 
     * @param sampleCount
     *            采样点个数
     * @param fetureCount
     *            多项式的系数
     * @param samples
     *            采样点集合
     **/
    private static Matrix leastsequare(int sampleCount, int fetureCout, List<Sample> samples) {
        // 构件 2*2矩阵 存储X，元素值都为1.0000的矩阵
        Matrix matrixX = DenseMatrix.Factory.ones(sampleCount, fetureCout);

        for (int i = 0; i < samples.size(); i++) {
            matrixX.setAsDouble(samples.get(i).getX(), i, 1);
        }

        // System.out.println(matrixX);
        // System.out.println("--------------------------------------");
        // 构件 2*2矩阵 存储X
        Matrix matrixY = DenseMatrix.Factory.ones(sampleCount, 1);

        for (int i = 0; i < samples.size(); i++) {
            matrixY.setAsDouble(samples.get(i).getY(), i, 0);
        }
        // System.out.println(matrixY);

        // 对X进行转置
        Matrix matrixXTrans = matrixX.transpose();
        // System.out.println(matrixXTrans);

        // 乘积运算：x*转转置后x:matrixXTrans*matrixX
        Matrix matrixMtimes = matrixXTrans.mtimes(matrixX);
        // System.out.println(matrixMtimes);

        // System.out.println("--------------------------------------");
        // 求逆
        Matrix matrixMtimesInv = matrixMtimes.inv();
        // System.out.println(matrixMtimesInv);

        // x转置后结果*求逆结果
        // System.out.println("--------------------------------------");
        Matrix matrixMtimesInvMtimes = matrixMtimesInv.mtimes(matrixXTrans);
        // System.out.println(matrixMtimesInvMtimes);

        // System.out.println("--------------------------------------");
        Matrix theta = matrixMtimesInvMtimes.mtimes(matrixY);
        // System.out.println(theta);

        return theta;
    }
}