距离本意就是两个目标的某一特征集从一个变成另一个需要的最小操作。广泛使用于相似度比较领域。机器学习中经常用的距离有:
1. 欧氏距离 ( Euclidean Distances)
2. 曼哈顿距离
3. 切比雪夫距离
4. 闵可夫斯基距离
5. 标准化欧氏距离
6. 马氏距离
7. 夹角余弦( Cosine Distance)
8. 汉明距离(Hamming Distance)
9. 杰卡德距离 & 杰卡德相似系数(Jaccard)
10. 相关系数 & 相关距离(pearson,Spearman, kendall tau correlation)
11. 信息熵(Kullback-Leibler Divergence / Relative Entropy)
部分可参考:http://www.cnblogs.com/heaad/archive/2011/03/08/1977733.html
1. Jaccard
-
Jaccard相似度有狭义和广义之分。
-
狭义:两个集合的交集数目除上两个集合的并集数目,即:

-
广义:元素的取值可以是实数。又称为Tanimoto系数,用EJ来表示,计算方式如下:
EJ(A,B)=(A*B)/(||A||^2+||B||^2-A*B)
其中A、B分别表示为两个向量,集合中每个元素表示为向量中的一个维度,在每个维度上,取值通常是[0, 1]之间的值,A*B表示向量乘积,||A||^2表示向量的模,即 ||A||^2 = sqrt (a1^2 + a2^2 + a3^2 + ......)。广义Jaccard相似度计算公式中,如果把分母的A*B去掉,并将||A||^2+||B||^2替换为(||A||^2)*(||B||^2),就转成了余弦相似度(cosine similarity)。 - Jacard 距离: d(x,y)= 1 - J(x,y).
2. Euclidean Distances
欧氏距离,即通常说的L2-范式(L2-norm)

3. Cosine Distance
先求余弦相似性,对于两个向量A和B,定义如下:
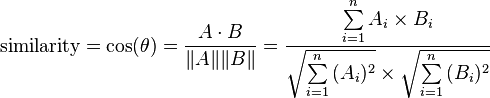
然后通过反余弦函数,求得的夹角θ,就是余弦距离。
4. Hamming Distance
汉明距更多的用于信号处理,表明一个信号变成另一个信号需要的最小操作(替换位),实际中就是比较两个比特串有多少个位不一样,简洁的操作时就是两个比特串进行异或之后包含1的个数。汉明距在图像处理领域也有这广泛的应用,是比较二进制图像非常有效的手段。计算一个数字的比特位包含1的个数有个小技巧:value &= value - 1这个运算的结果就是把value最后一个1去掉,循环进行运算直到value等于0(所有的1都被去掉)就可以知道vaule拥有多少个1了。
参考:http://zh.wikipedia.org/wiki/%E6%B1%89%E6%98%8E%E8%B7%9D%E7%A6%BB