百度PaddlePaddle入门-6 (Numpy应用)

---

 

线性代数

Numpy中实现了线性代数中常用的各种操作，并形成了numpy.linalg线性代数相关的模块。其中包括：

• diag 以一维数组的形式返回方阵的对角线（或非对角线）元素，或将一维数组转换为方阵（非对角线元素为0）
• dot 矩阵乘法
• trace 计算对角线元素的和
• det 计算矩阵行列式
• eig 计算方阵的特征值和特征向量
• inv 计算方阵的逆

# 矩阵相乘
a = np.arange(12)
b = a.reshape([3, 4])
c = a.reshape([4, 3])
# 矩阵b的第二维大小，必须等于矩阵c的第一维大小
d = b.dot(c) # 等价于 np.dot(b, c)
print('a: 
{}'.format(a))
print('b: 
{}'.format(b))
print('c: 
{}'.format(c))
print('d: 
{}'.format(d))

a: 
[ 0  1  2  3  4  5  6  7  8  9 10 11]
b: 
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
c: 
[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]
d: 
[[ 42  48  54]
 [114 136 158]
 [186 224 262]]
下面为补充资料：

设A为

的矩阵，B为

的矩阵，那么称

的矩阵C为矩阵A与B的乘积，记作

，其中矩阵C中的第

行第

列元素可以表示为： ^[1] 

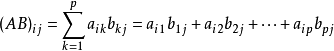
如下所示：

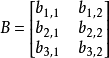
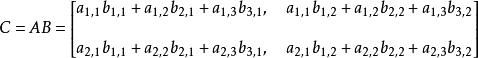
# numpy.linalg  中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的东西
# np.linalg.diag 以一维数组的形式返回方阵的对角线（或非对角线）元素，
# 或将一维数组转换为方阵（非对角线元素为0）
e = np.diag(d)
f = np.diag(e)
print('d: 
{}'.format(d))
print('e: 
{}'.format(e))
print('f: 
{}'.format(f))

d: 
[[ 42  48  54]
 [114 136 158]
 [186 224 262]]
e: 
[ 42 136 262]
f: 
[[ 42   0   0]
 [  0 136   0]
 [  0   0 262]]

# trace, 计算对角线元素的和
g = np.trace(d)
g

440

# det，计算行列式
h = np.linalg.det(d)
h

1.3642420526593978e-11

一个n×n的方阵A的行列式记为det(A)或者|A|，一个2×2矩阵的行列式可表示如下：

把一个n阶行列式中的元素a_ij所在的第i行和第j列划去后，留下来的n-1阶行列式叫做元素a_ij的余子式,记作M_ij。记A_ij=(-1)^i+jM_ij，叫做元素a_ij的代数余子式。例如：

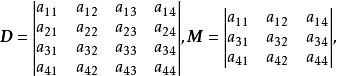
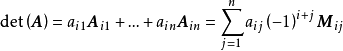
一个n×n矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和，即 ^[1]  :

# eig，计算特征值和特征向量
i = np.linalg.eig(d)
i

(array([4.36702561e+02, 3.29743887e+00, 3.13152204e-14]),
 array([[ 0.17716392,  0.77712552,  0.40824829],
        [ 0.5095763 ,  0.07620532, -0.81649658],
        [ 0.84198868, -0.62471488,  0.40824829]]))
设 A 是n阶方阵，如果存在数m和非零n维列向量 x，使得 Ax=mx 成立，则称 m 是矩阵A的一个特征值（characteristic value)或本征值（eigenvalue)。

# inv，计算方阵的逆
tmp = np.random.rand(3, 3)
j = np.linalg.inv(tmp)
tmp, j

(array([[0.06156638, 0.49923069, 0.24846698],
        [0.32714403, 0.00291609, 0.29544213],
        [0.98688912, 0.23833271, 0.73339648]]),
 array([[-1.69687265, -7.62795567,  3.64773546],
        [ 1.28349546, -4.97212032,  1.56813898],
        [ 1.86628413, 11.88029355, -4.05462716]]))

---

Numpy保存和导入文件

Numpy还可以方便的进行文件读写，比如对于下面这种格式的文本文件：

# 使用np.fromfile从文本文件'housing.data'读入数据
# 这里要设置参数sep = ' '，表示使用空白字符来分隔数据
# 空格或者回车都属于空白字符，读入的数据被转化成1维数组
d = np.fromfile('./work/housing.data', sep = ' ')
d,d.size,d.shape

(array([6.320e-03, 1.800e+01, 2.310e+00, ..., 3.969e+02, 7.880e+00,
        1.190e+01]), 7084, (7084,))
注意到shape输出的形式。
Numpy还提供了save和load接口，直接将数组保存成文件(保存为.npy格式)，或者从.npy文件中读取数组。

# 产生随机数组a
a = np.random.rand(3,3)
np.save('a.npy', a)

# 从磁盘文件'a.npy'读入数组
b = np.load('a.npy')

# 检查a和b的数值是否一样
check = (a == b).all()
check

True