树状数组是对一个数组改变某个元素和求和比较实用的数据结构。两中操作都是O(logn)。
在解题过程中,我们有时需要维护一个数组的前缀和S[i]=A[1]+A[2]+...+A[i]。
但是不难发现,如果我们修改了任意一个A[i],S[i]、S[i+1]...S[n]都会发生变化。
可以说,每次修改A[i]后,调整前缀和S[]在最坏情况下会需要O(n)的时间。
当n非常大时,程序会运行得非常缓慢。
因此,这里我们引入“树状数组”,它的修改与求和都是O(logn)的,效率非常高。
【理论】
为了对树状数组有个形 象的认识,我们先看下面这张图。
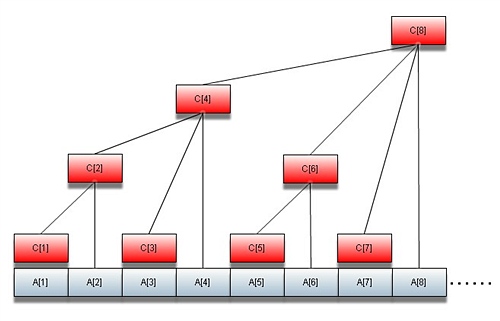
如图所示,红色矩形表示的数组C[]就是树状数组。
这里,C[i]表示A[i-2^k+1]到A[i]的和,而k则是i在二进制时末尾0的个数,
或者说是i用2的幂方和表示时的最小指数。
( 当然,利用位运算,我们可以直接计算出2^k=i&(i^(i-1)) )
同时,我们也不难发现,这个k就是该节点在树中的高度,因而这个树的高度不会超过logn。
所以,当我们修改A[i]的值时,可以从C[i]往根节点一路上溯,调整这条路上的所有C[]即可,
这个操作的复杂度在最坏情况下就是树的高度即O(logn)。
另外,对于求数列的前n项和,只需找到n以前的所有最大子树,把其根节点的C加起来即可。
不难发现,这些子树的数目是n在二进制时1的个数,或者说是把n展开成2的幂方和时的项数,
因此,求和操作的复杂度也是O(logn)。
接着,我们考察这两种操作下标变化的规律:
首先看修改操作:
已知下标i,求其父节点的下标。 我们可以考虑对树从逻辑上转化:
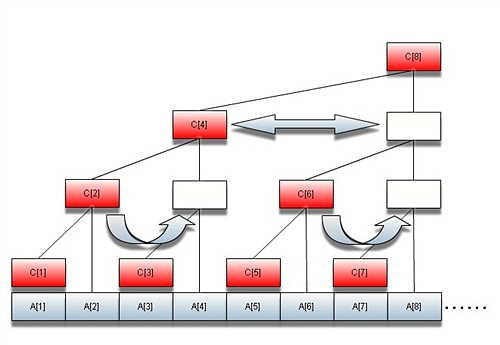 如图,我们将子树向右对称翻折,虚拟出一些空白结点(图中白色),将原树转化成完全二叉树。
如图,我们将子树向右对称翻折,虚拟出一些空白结点(图中白色),将原树转化成完全二叉树。
有图可知,对于节点i,其父节点的下标与翻折出的空白节点下标相同。
因而父节点下标 p=i+2^k (2^k是i用2的幂方和展开式中的最小幂,即i为根节点子树的规模)
即 p = i + i&(i^(i-1)) 。
接着对于求和操作:
因为每棵子树覆盖的范围都是2的幂,所以我们要求子树i的前一棵树,只需让i减去2的最小幂即可。
即 p = i - i&(i^(i-1)) 。
至此,我们已经比较详细的分析了树状数组的复杂度和原理。
在最后,我们将给出一些树状数组的实现代码,希望读者能够仔细体会其中的细节。
【代码】
求最小幂2^k:
|
int Lowbit(int t) { return t & ( t ^ ( t - 1 ) ); } |
求前n项和:
|
int Sum(int end) { int sum = 0; while(end > 0) { sum += in[end]; end -= Lowbit(end); } return sum; } |
对某个元素进行加法操作:
void plus(int pos , int num)
{
while(pos <= n)
{
in[pos] += num;
pos += Lowbit(pos);
}
}