算法总结-广搜(BFS:breadth-first search)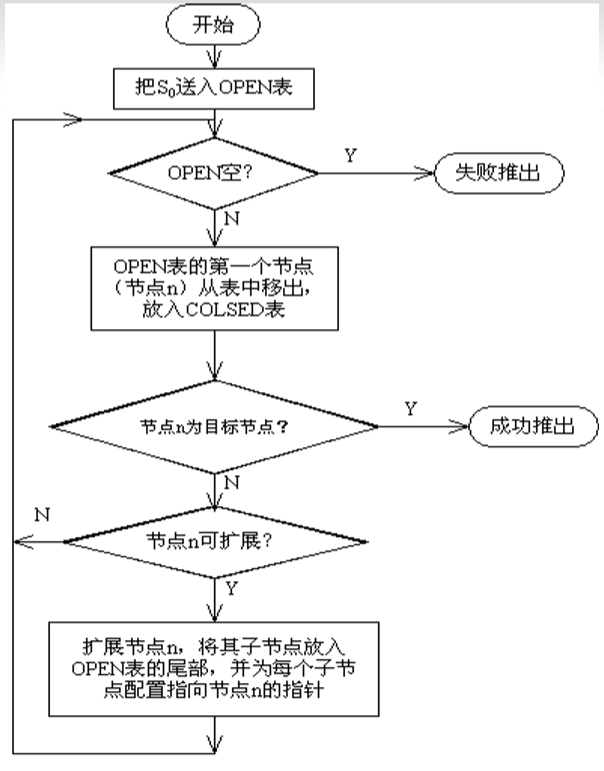
广度优先搜索算法(用QUEUE)
- 把初始节点S0放入Open表(待扩展表)中;
- 如果Open表为空,则问题无解,失败退出;
- 把Open表的第一个节点取出放入Closed表,并记该节点为n;
- 考察节点n是否为目标节点。若是,则得到问题的解,成功退出;
- 若节点n不可拓展,则转第2步;
- 扩展节点n,将其不在Closed表和Open表的子节点(判重)放入Open表的尾部,并为每一个子节点设置指向父节点的指针(或记录节点的层次),然后转第2步;
(详见刘家瑛课程PPT,结合Catch That Cow)
广搜和深搜的比较
广搜一般用于状态表示比较简单、求最优策略的问题。一层一层的搜,每一条路径的搜索进度都是一样的,因此需要用到队列的知识,不需要使用递归.
优点:是一种完备策略,即只要问题有解,它就一定可以找到解 。并且,广度优先搜索找到的解,还一定是路径最短的解。
缺点:盲目性较大,尤其是当目标节点距初始节点较远时,将产生许多无用的节点,因此其搜索效率较低。需要保存所有扩展出 的状态,占用的空间大。
深搜几乎可以用于任何问题,一条路搜到底,不能再往下了,就回溯一步,需要用到递归,且只需要保存从起始状态到当前状态路径上的节点。
因此dfs适合那些求可行性路径数目的,而bfs适合求最短路径之类的(因为一旦搜到,就是最短)。
——根据题目要求凭借自己的经验和对两个搜索的熟练程度做出选择 。
数据结构:使用队列queue完成bfs,通常需要点结构来存储结点信息
bool vis[5][5];//记录访问数组 queue <Node> q; struct Node { int x; int y; };
bfs():广度遍历地图
Node bfs()//返回终点 { queue <Node> q; Node cur, next; cur.x = 0; cur.y = 0;//初始结点信息 q.push(cur);//初始结点入队, while (!q.empty()) //开启bfs过程 { cur = q.front();//取队头结点 q.pop(); if (cur.x == 终点.x && cur.y == 终点.y) return cur;//过程结束条件 int i, nx, ny;//新的待遍历结点 for (i = 0; i < 4; i++) { nx = cur.x + dx[i]; ny = cur.y + dy[i]; if (judge(nx, ny))continue; //不可以走,边界或者已遍历等 next = cur; next.x = nx; next.y = ny; q.push(next);//新结点入队 } } }
广搜例题-poj3278 Catch That Cow
#include<iostream> #include<cstring> #include<queue> using namespace std; int N, K;//农夫起点和牛的位置 const int MAXN = 100000;//最大坐标范围 int visited[MAXN + 10];//判重标记,visited[i]=true表示i已经扩展过 struct Step//一个坐标 { int x;//位置 int steps;//达到x所需的步数,即找到牛所需要的时间 Step(int xx,int s):x(xx),steps(s){}//构造函数 }; queue<Step> q;//队列,即Open表 int main() { cin >> N >> K; memset(visited, 0, sizeof(visited)); q.push(Step(N, 0));//将农夫起点加入扩展队列 visited[N] = 1;//标记N,起点位置已访问 while (!q.empty())//Open表如果不为空,则一直扩展,直到Open表为空或者扩展到目标结点 { Step s = q.front();//读取队头元素 if (s.x == K)//找到目标 { cout << s.steps << endl; return 0;//直接结束 } else { if (s.x - 1 >= 0 && !visited[s.x - 1])//能往左边走且左边的结点还没有被访问过 { q.push(Step(s.x - 1, s.steps + 1)); visited[s.x - 1] = 1; } if (s.x + 1 <= MAXN && !visited[s.x + 1])//能往右边走且右边的结点还没有被访问过 { q.push(Step(s.x + 1, s.steps + 1)); visited[s.x + 1] = 1; } if (s.x * 2 <= MAXN && !visited[s.x * 2])//能往左边走一倍且左边的结点还没有被访问过 { q.push(Step(s.x * 2, s.steps + 1)); visited[s.x * 2] = 1; } q.pop();//队头元素出列 } } return 0; }

#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #include<queue> using namespace std; int vis[100005] = { 0 }; struct Node { int x, t; }; queue<Node>q; bool valid(int x) { return (x >= 0 && x <= 100000); } int main() { int n, k; scanf("%d%d", &n, &k); Node s; s.x = n; s.t = 0; vis[n] = 1; q.push(s); while (!q.empty()) { Node cur = q.front(); q.pop(); if (cur.x == k) { printf("%d", cur.t); return 0; } Node tmp; if (valid(cur.x + 1) && !vis[cur.x + 1]) { tmp.x = cur.x + 1; vis[cur.x + 1] = 1; tmp.t = cur.t + 1; q.push(tmp); } if (valid(cur.x * 2) && !vis[cur.x * 2]) { tmp.x = cur.x * 2; tmp.t = cur.t + 1; vis[cur.x * 2] = 1; q.push(tmp); } if (valid(cur.x - 1) && !vis[cur.x - 1]) { tmp.x = cur.x - 1; vis[cur.x - 1] = 1; tmp.t = cur.t + 1; q.push(tmp); } } return 0; }
广搜模板(地图寻路)
struct st{ ... }; queue<st> q; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; void bfs(){ q.push(start_st); while(!q.empty()){ st tmp=q.front(); q.pop(); for(int i = 0; i < 4;++i){ if(...) q.push(st(...)); } } }
寻路例题 POJ 3984 迷宫问题
#include <iostream> #include <stdio.h> #include <string.h> #include <queue> using namespace std; bool vis[5][5]; int a[5][5]; int dx[4] = {0,1,0,-1}; int dy[4] = {1,0,-1,0}; struct Node{ int x; int y; int s; short l[30]; }; bool Noway(int x,int y) { if(x<0 || x>=5 || y<0 || y>=5) return true; if(vis[x][y]) return true; if(a[x][y]==1) return true; return false; } Node bfs() { queue <Node> q; Node cur,next; cur.x = 0; cur.y = 0; cur.s = 0; vis[cur.x][cur.y] = true; q.push(cur); while(!q.empty()){ cur = q.front(); q.pop(); if(cur.x==4 && cur.y==4) return cur; int i,nx,ny; for(i=0;i<4;i++){ nx = cur.x + dx[i]; ny = cur.y + dy[i]; if(Noway(nx,ny))continue;//不可以走 vis[nx][ny] = true; next = cur; next.x = nx; next.y = ny; next.s = cur.s + 1; next.l[cur.s] = i; q.push(next); } } return cur; } int main() { int i,j; for(i=0;i<5;i++){ //读入迷宫 for(j=0;j<5;j++){ scanf("%d",&a[i][j]); } } memset(vis,0,sizeof(vis)); Node ans = bfs(); int x,y; x = 0,y = 0; for(i=0;i<=ans.s;i++){ printf("(%d, %d) ",x,y); x+=dx[ans.l[i]]; y+=dy[ans.l[i]]; } return 0; }
双向广搜(DFBS)
定义:从两个方向以广度优先的顺序同时扩展。
比较:
- DBFS算法相对于BFS算法来说,由于采用了双向扩展的方式,搜索树的宽度得到了明显的减少,时间复杂度和空间复杂度上都有提高!
- 假设1个结点能扩展出n个结点,单向搜索要m层能找到答案,那么扩展出来的节点数目就是: (1-nm)/(1-n) 。
- 双向广搜,同样是一共扩展m层,假定两边各扩展出m/2层,则总结点数目 2 * (1-nm/2)/(1-n)。
- 每次扩展结点总是选择结点比较少的那边进行扩展,并不是机械的两边交替。
框架:
一、双向广搜函数:
void dbfs() {
- 将起始节点放入队列q0,将目标节点放入队列q1;
- 当两个队列都未空时,作如下循环:如果队列q0未空,不断扩展q0直到为空;
- 如果队列q0里的节点比q1中的少,则扩展队列q0;
- 否则扩展队列q1
- 如果队列q0未空,不断扩展q0直到为空;
- 如果队列q1未空,不断扩展q1直到为空;
}
二、扩展函数:
int expand(i) //其中i为队列的编号,0或1
{
- 取队列qi的头结点H;
- 对H的每一个相邻节点adj:
1.如果adj已经在队列qi之中出现过,则抛弃adj;
2.如果adj在队列qi中未出现过,则:
1) 将adj放入队列qi;
2) 如果adj 曾在队列q1-i中出现过, 则:输出找到的路径
}
需要两个标志序列,分别记录节点是否出现在两个队列中
