3.4用for语句实现循环结构
什么是循环结构
for语句
1.什么是循环结构?
循环结构又称为重复结构,是利用计算机运算速度快以及能进行逻辑控制的特点来重复执行某些操作。重复执行的部分称为循环体。
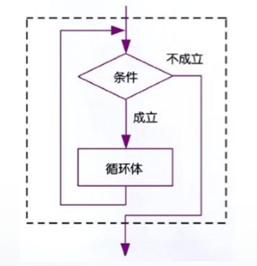
2.for语句
格式:当步长为1时,表达式2可省略。
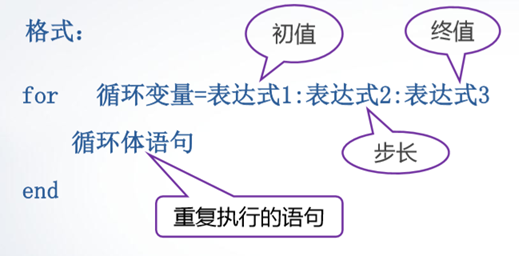
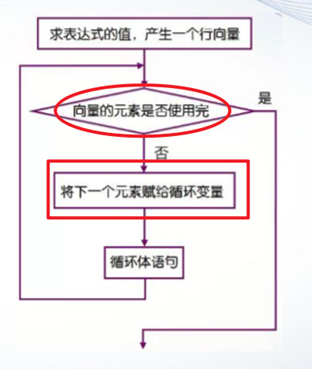
说明:
1、 for语句针对向量的每一个元素执行一次循环体。

2、退出循环之后,循环变量的值就是向量中最后的元素值。

3、当向量为空时,循环体一次也不执行。

计算圆周率π
(1)利用无穷级数展开式求π 的近似值。(迭代法)
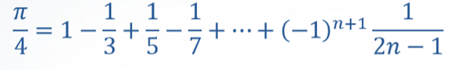
- 这是求n个数之和的累加问题,可用以下递推式来描述:
yi=yi-1+fi (y0=0) // 上次循环的累加和加上当前的累加项f
- 可用以下赋值语句来实现。
y=y+f
- 其中累加项f的符号可用以下赋值语句来实现(每循环一次反号一次)。
g=-g
- 累加项f就可用以下赋值语句来实现。
f=g/(2*i-1)
程序:
y=0; //y存放最后的累加值
g=-1; //类加项的符号
n=input('n=?’);
for i=1:n
g=-g; //每一次先求符号
y=y+g/(2*i-1); //累加到y中
end
pai=4*y
迭代法:设置一个变量(称为迭代变量y),其值在原来值得基础上按递推关系计算出来。迭代法就用到了循环的概念,把求n个数之和的问题转化为求两个数之和的重复。
用向量求和的方法实现程序:
n=input('n=?');
x=1:2:(2*n-1); //生成一个向量x
y=(-1).^(2:n+1)./x; //y的各累加项
pai=sum(y)*4 //sun函数
(2)利用定积分的近似值求π 的近似值。
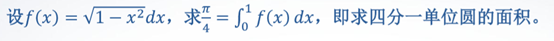
求函数f(x)在[a,b]上的定积分,就是求曲线y=f(x)与直线x=a,x=b,y=0所围成的曲边梯形的面积。近似求出每个小曲边梯形面积,然后将n个小曲边梯 形的面积加起来,就得到总面积,也就是定积分的近似值。

a=0;
b=1;
n=input('n=?');
h=(b-a)/n; //求宽度
x=a:h:b; //n+1个自变量的值
f=sqrt(1-x.*x); //点乘
s=[];
for k=1:n
s1=(f(k)+f(k+1))*h/2; //小梯形的面积
s=[s,s1]; //s1追加到s中去
end
pai=4*sum(s)
//当然matlab也提供了关于数值积分的标准函数
(3)利用蒙特卡洛法求π 的近似值。
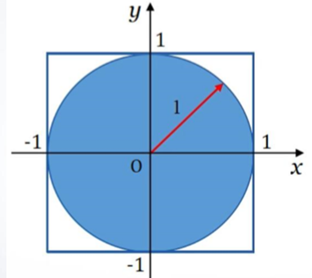
在正方形内随机投点,设点落在圆内的概率为P。
P=π /4 ——>π =4P
P=落在圆内的点数/所投点的总数
所投的点落在圆内的充要条件是x2+y2≤1。
s=0;
n=input('n=?');
for i=1:n
x=rand(1);
y=rand(1); //x和y取一个随机数
if x*x+y*y<=1
s=s+1;
end
end
pai=s/n*4
按照Matlab的定义,for语句的循环变量也可以是一个列向量。
for 循环变量=矩阵表达式
循环体语句
end
执行过程是依次将矩阵的各列元素赋给循环变量,然后执行循环体语句,直到各列元素处理完毕循环结束。
s=0;
a=[12,13,14;15,16,17;18,19,20;21,22,23]
for k=a //三列
s=s+k; //一列累加到s中去
end
s
s=
39
48
57
66
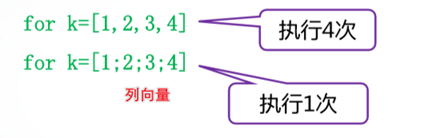
下面两个for语句引导的循环结构,其循环体执行的次数相同吗?如果不相同,分别是多少?
3.5 用while语句实现循环结构
while语句
break语句和continue语句
循环的嵌套
For语句用于事先确立循环次数的较方便。
1.while语句
While通过判断循环条件是否成立来决定是否要继续循环的一种循环控制语句。也叫条件循环语句。
格式:

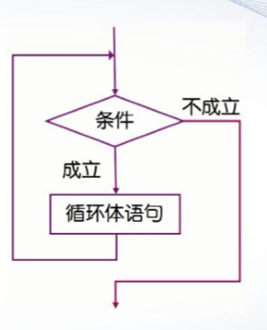
例1 从键盘输入若干个数,当输入0时结束输入,求这些数的平均值和它们之和。
msum=0; //累加和
n=0; //输入数值的个数
x=input('Enter a number (end in 0):');
while x~=0
msum=msum+x;
n=n+1;
x=input('Enter a number (end in 0):');
end
if n>0
msum //输出累加值
mean=msum/n //输出平均值mean
end
while语句多用于循环次数不确定的情况,而对于循环次数确定的情况,使用for语句更方便。
针对不同情况可以选择不同的循环语句,但从功能上讲两种循环语句可以相互替代。
2.break语句和continue语句——流程转向语句
一般与if语句配合使用。
break语句用来跳出循环体,结束整个循环。
continue语句用来结束本次循环,接着进行下一次是否执行循环的判断。只是结束本次循环。
例2 求[100,200]之间第一个能被21整除的整数。
for n=100:200
if rem(n,21)~=0
continue
end
n //第一个能被21整除的整数
break
end
3.循环的嵌套
如果一个循环结构的循环体又包括一个循环结构,就称为循环的嵌套,或称为多重循环结构。处于内部的循环叫做内循环,处于外部的循环叫做外循环。
例3 用筛选法求某自然数范围内的全部素数。(素数时大于1,而且是除了1和他本身之外不能被其他任何整数所整除的整数)
筛选法求素数的基本思想:要找出2~m之间的全部素数,首先在2~m中划去2的倍数(不包括2),然后划去3的倍数(不包括3),由于4已被划去,再找5的倍数(不包括5),…,直到再划去不超过根号m的倍数,剩下的数就都是素数了。
m=input('m=');
p=1:m; //p包含1-m的m个元素
p(1)=0; //表示1不是素数
for i=2:sqrt(m)
for j=2*i:i:m
p(j)=0; //p中以i的倍数为序号的元素赋值为0
end
end
n=find(p~=0); //调用find函数,找出p中非零元素的下标赋给变量n
p(n) //输出所有素数
TIP:
1.循环语句可以互相嵌套
2.内循环必须包含在外层循环的循环体中,注意内外循环之间的关系。不允许出现交叉的现象。