结对开发之返回一个二维整数数组中最大联通子数组的和

一、题目要求

输入一个二维整形数组，数组里有正数也有负数。
二维数组首尾相接，象个一条首尾相接带子一样。
数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。
求所有子数组的和的最大值。
要求时间复杂度为O(n)题目:返回一个二维整数数组中最大子数组的和

二、解题思路

      先对二维数组进行了重构，形成一个环状二维数组，然后再用求二维数组子矩阵最大和的方法求得最终结果。

三、程序代码

#include<iostream.h>
int main(int argc, char* argv[])
{
    int i,j;
    int a[3][5]={{1,-2,3},{1,-3,2},{4,-4,5}};
    int b[3][5];
    for(i=0;i<3;i++)
    {
     for(j=0;j<2;j++)
        a[i][j+3]=a[i][j];
    }
    int max=a[0][0];
    cout<<"初始二维数组为："<<endl;
    for(i=0;i<3;i++)
    {
        for(j=0;j<3;j++)
        {
            cout<<a[i][j]<<' ';
        }
        cout<<endl;
    }
    cout<<"重构后环形数组为："<<endl;
    for(i=0;i<3;i++)
    {
        for(j=0;j<5;j++)
        {
            cout<<a[i][j]<<' ';
        }
        cout<<endl;
    }


    for(i=0;i<1;i++)
    {
        b[0][0]=a[0][0];
        for(j=0;j<5;j++)
        {
            if(a[0][j-1]<0)
            {
                b[0][j]=a[0][j];
            }
            else
            {
                b[0][j]=b[0][j-1]+a[0][j];
            }        
        }
    }
    for(i=1;i<3;i++)
    {
        for(j=0;j<1;j++)
        {
            if(a[i-1][0]<0)
            {
                b[i][0]=a[i][0];
            }
            else
            {
                b[i][0]=b[i-1][0]+a[i][0];
            }
        }
    }
    for(i=1;i<3;i++)
    {
        for(j=1;j<5;j++)
        {
            if(b[i-1][j-1]<0)
            {
                if(b[i-1][j]>=0&&b[i][j-1]>=0)
                {
                    if(b[i][j-1]>=b[i-1][j])
                    {
                        b[i][j]=b[i][j-1]+a[i][j];
                    }
                    else
                    {
                        b[i][j]=b[i-1][j]+a[i][j];
                    }
                }
                else if(b[i-1][j]>=0&&b[i][j-1]<=0)
                {
                    b[i][j]=b[i-1][j]+a[i][j];
                }
                else if(b[i-1][j]<=0&&b[i][j-1]>=0)
                {
                    b[i][j]=b[i][j-1]+a[i][j];
                }
                else
                {
                    b[i][j]=a[i][j];
                }
            }
            else
            {
                if(b[i-1][j]>=0&&b[i][j-1]>=0)
                {
                    b[i][j]=a[i][j]+b[i-1][j]+b[i][j-1]-b[i-1][j-1];
                }
                else if(b[i-1][j]>=0&&b[i][j-1]<=0)
                {
                    b[i][j]=a[i][j]+b[i-1][j]-b[i-1][j-1];
                }
                else if(b[i-1][j]<=0&&b[i][j-1]>=0)
                {
                    b[i][j]=a[i][j]+b[i][j-1]-b[i-1][j-1];
                }
                else
                {
                    b[i][j]=a[i][j];
                }
            }
        }
    }
    cout<<"子矩阵的和数组为："<<endl;
    for(i=0;i<3;i++)
    {
        for(j=0;j<5;j++)
        {
            cout<<b[i][j]<<" ";
        }
        cout<<endl;
    }
    cout<<endl;
    for(i=0;i<3;i++)
    {
        for(j=0;j<5;j++)
        {
            if(b[i][j]>max)
                max=b[i][j];
        }
    }
    cout<<"最大子矩阵和为："<<max<<endl;
    return 0;      

}

四、运行截图

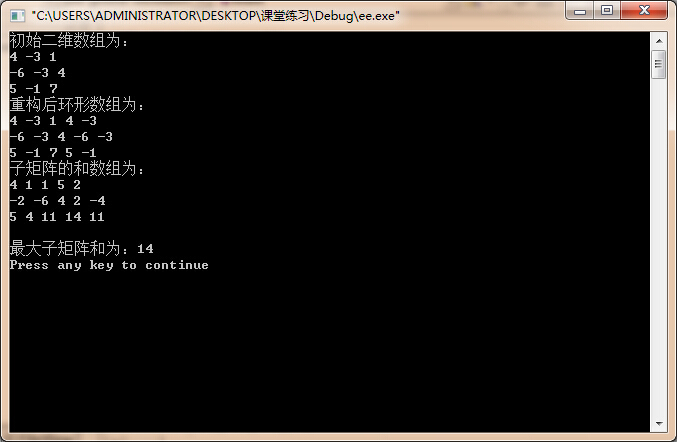
五、实验总结

    求二维数组最大子矩阵的和，求环形一维数组的最大子数组的和，环形一维时，我们采用了跨越首尾和不跨越首尾两种情况，发现这种方法不适用于二维，所以采用了重构数组的方法，转化成非环形，然后求二维最大子数组的和。开始在循环条件那儿遇到了问题，后来我们两个一起解决了，这次合作让我体会到了搭档的重要性，总之，这次结对开发很成功，以后继续努力。