20172332 2017-2018-2 《程序设计与数据结构》第八周学习总结
教材学习内容总结
第十二章 优先队列与堆
-
1.最小堆:具有两个附加属性的一棵二叉树。
- ①他是一棵完全树
- ②对每一结点,它小于或等于其左孩子和右孩子。
-
2.最小堆将其最小元素存储在该二叉树的根处,且其根的两个孩子同样也是最小堆。
-
3.addElement操作:
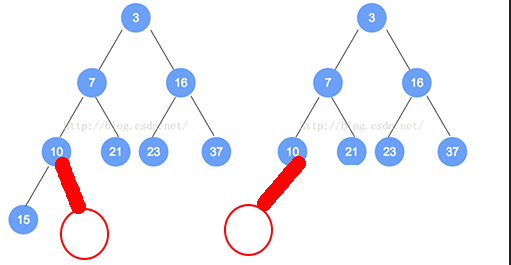
- ①维持该堆的完全性属性和有序属性,所以插入的元素位置只存在一个正确的位置,要不然在h层左边的下一个空位置,要不然在h+1层左边的第一个位置。
下图中,左图这种类型的为h层左边的下一个空位置,右图这种类型的为h+1层左边的第一个位置。
- ①维持该堆的完全性属性和有序属性,所以插入的元素位置只存在一个正确的位置,要不然在h层左边的下一个空位置,要不然在h+1层左边的第一个位置。
- ②添加的为Comparable元素。
- ③添加之后进行排序(过程名叫筛选)
- ④在堆实现中,一般会对树中的最末一个结点(最末一片叶子),进行跟踪记录。
-
4.removeMin操作:
- ①维持该堆的完全性,(删除最小的也就是删除根)能替换根的合法元素只有一个就是最末一片叶子上存储的元素。
- ②删除之后进行排序(过程名叫筛选)
-
5.findMin操作:
- 最小堆中的最小元素存储在根中,所以只需要返回存储在根中的元素。
-
6.最大堆的定义与性质同理可得。
-
7.优先级队列:遵循两个排序规则的集合。
- ①具有更高优先级的项目在先。
- ②具有相同优先级的项目使用先进先出方法来确定其排序。
- ③解决方案:(1)使用队列列表;(2)使用最小堆。
-
8.用链表实现堆:为了在插入元素后能够向上遍历该树,对BinaryTreeNode进行扩展并添加一个双亲指针。
-
9.用数组实现堆:首先检查可用空间,如有需要进行扩容。
-
9.链表实现和数组实现的addElement操作的时间复杂度同为O(log n)。
-
10.链表实现和数组实现的removeMin操作的复杂度同为O(log n)。
-
11.findMin操作只需要返回一个引用,因此复杂度为O(1)。
-
12.堆排序。
- 最小堆排序结果为升序排序,最大堆排序结果为降序排序。
- 复杂度为O(n log n)
- heapSort方法的两部分构成:添加列表的每个元素,然后一次删除一个元素。
- 也可以使用要排序的数组来构建一个堆,通过互换得出排序结果。
-
13.二叉树的数组实现中,树的根位于位置0处,对于每一个结点n,n的左孩子将位于数组的2n+1位置处,n的右孩子将位于数组的2(n+1)位置处。
教材学习中的问题和解决过程
- 问题1:对getNextParentAdd操作代码的理解。
HeapNode<T> result = lastNode;
while ((result != root) && (result.getParent().getLeft() != result))
result = result.getParent();
if (result != root)
if (result.getParent().getRight() == null)
result = result.getParent();
else {
result = (HeapNode<T>) result.getParent().getRight();
while (result.getLeft() != null)
result = (HeapNode<T>) result.getLeft();
}
else
while (result.getLeft() != null)
result = (HeapNode<T>) result.getLeft();
return result;
- 问题1解决方案:这个方法是为了得到插入结点的双亲结点,看代码会很抽象,插入之前的堆,也就几种情况,可以一个一个跟着代码走一边,了解过程。
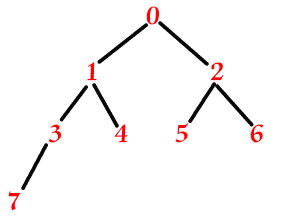
- ①下图中7的结点为lastNode,看while循环的判断条件,该结点不为根结点,但是该结点的双亲结点的左孩子是它自己,所以不进入循环。看if语句块的判断条件,首先不为根结点,该结点的双亲结点的右孩子也就是7结点的兄弟是空的,所以返回的值为7结点的双亲结点,从图中可以很明显的看出,插入元素位置的双亲结点的确是7结点的双亲结点。
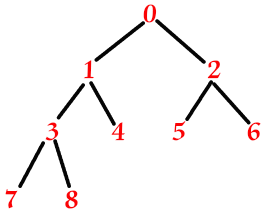
- ②下图中8的结点为lastNode,看while循环的判断条件,该结点不为根结点,该结点的双亲结点的左孩子不是它自己,所以进入循环。result等于8结点的双亲结点,也就是3结点,看while循环的判断条件,该结点不为根结点,该结点的双亲结点的左孩子是它自己,所以跳出循环。看if语句块的判断条件,首先不为根结点,该结点的双亲结点的右孩子不为空,所以result等于该结点的双亲结点的右孩子,也就是3结点的右兄弟4结点,它的左孩子为空所以,插入元素的位置的双亲结点为4结点,从图中也可看出。
- ③这种情况同①,可以算作一种情况
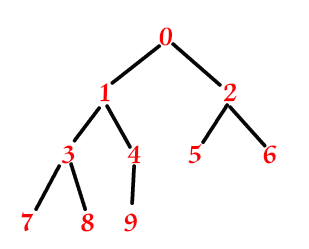
- ④下图中10的结点为lastNode,看while循环的判断条件,会发现要经过两次循环,最终result等于1的结点,然后进入if语句块,1结点的双亲结点的右孩子不为空,所以进入else,result等于1结点的双亲结点的右孩子,也就是它自己的右兄弟,也就是2结点。看while循环的判断条件,2的左孩子不为空,满足条件,所以进入循环,得出result为5结点,很显然与图中符合一致。
- ⑤有一种特殊情况,就是只有根的情况,故lastNode为根结点,插入元素就是根结点的孩子,所以返回值就是根结点。
- 右子树的情况与上面几种一样,故不再探究。
- 问题2:对heapifyAdd操作的代码理解。
private void heapifyAdd()
{
T temp;
int next = count - 1;
temp = tree[next];
while ((next != 0) &&
(((Comparable)temp).compareTo(tree[(next-1)/2]) < 0))
{
tree[next] = tree[(next-1)/2];
next = (next-1)/2;
}
tree[next] = temp;
}
- 问题2解决方案:将元素插入后,为了保持堆的有序性,会进行排序(筛选的过程)。找到插入元素的双亲结点进行比较,把插入元素放入temp暂存,如果比双亲结点小(或者大),则把双亲结点向下移(或者不动),直到找到双亲结点不动的情况,则找到该插入元素的位置,把temp给双亲结点的孩子。
代码调试中的问题和解决过程
- 无。
代码托管
22440
上周考试错题总结
-
1.Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.
-
A .True
-
B .Flase
-
答案:B
-
分析:插入元素只有一个正确的位置的原因是因为它是一棵二叉完全树,而不是因为是一颗二叉搜索树。
-
2.After one pass on the numbers ( 5 3 9 5 ), what would be the result if you were to use Bubble Sort?
-
A .5 3 5 9
-
B .5 5 3 9
-
C .3 5 5 9
-
D .9 5 5 3
-
答案:C
-
分析:按索引值来走,先是比a[0]与a[1],需要把他俩交换,得到3 5 9 5,再比较a[1]和a[2],不动,再比较a[2]和a[3],需要交换,所以得到3 5 5 9
点评过的同学博客和代码
其他(感悟、思考等,可选)
- 堆是树的引申,并不难理解
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 2/2 | |
| 第二周 | 1010/1010 | 1/2 | 10/12 | |
| 第三周 | 651/1661 | 1/3 | 13/25 | |
| 第四周 | 2205/3866 | 1/4 | 15/40 | |
| 第五周 | 967/4833 | 2/6 | 22/62 | |
| 第六周 | 1680/6513 | 1/7 | 34/96 | |
| 第七周 | 2196/8709 | 1/8 | 35/131 | |
| 第八周 | 1952/10661 | 2/9 | 49/180 |
-
计划学习时间:20小时
-
实际学习时间:49小时
-
改进情况:这周有实验所以花费的时间很多。