编程判断2个链表是否相交(假设2个链表均不带环)
解法二:
利用计数的方法,如果我们能够判断2个链表中是否存在地址一致的节点,就可以知道这2个链表是否相交。一个简单的做法是对第一个链表的节点地址进行hash排序,建立hash表,然后针对第二个链表的每个节点的地址查询hash表,如果在hash表中出现,那么说明有共同的节点,时间复杂度为O(L1+L2),但是同时要附加O(L1)的存储空间。
解法3:转化为另一已知问题
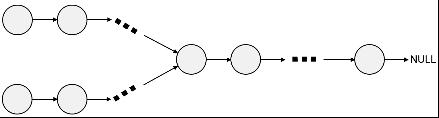
由于2个链表都没有环,我们可以把第二个链表接在第一个链表后面,如果得到的链表有环,则说明2个链表相交。
这样,我们就把问题转换为判断一个链表是否有环。
那么“两个无环单向链表”画出来只可能是2条不相干的链表或一个”Y”字形。我们只需从第二个链表开始遍历,看是否会回到起点就可以判断出来,最后,当然可别忘了恢复原来的状态,
解法4:
用指针p1、p2分别指向两个链表头,不断后移;最后到达各自表尾时,若p1==p2,那么两个链表必相交
复杂度为O(L1+L2),比解法3更好。
求相交的第一个节点:
对于相交的第一个结点,则可求出两个链表的长度,然后用长的减去短的得到一个差值 K,然后让长的链表先遍历K个结点,然后两个链表再开始比较。还可以这样:其中一个链表首尾相连,检测另外一个链表是否存在环,如果存在,则两个链表相交,而检测出来的依赖环入口即为相交的第一个。
#include<iostream> using namespace std; typedef struct Node { int data; Node* next; Node(int data) { this->data=data; } Node(){} }*LinkList; void initList(LinkList &list) { list=new Node(); list->next=NULL; } void insertList(LinkList &list) { int val; Node *tail=list; while(tail->next!=NULL) tail=tail->next; while(cin>>val && val!=-1) { Node *p=new Node(val); p->next=NULL; tail->next=p; tail=tail->next; } } void listTraverse(LinkList &list) { Node *p=list->next; while(p) { cout<<p->data<<ends; p=p->next; } } int main() { LinkList L; initList(L); insertList(L); listTraverse(L); cout<<endl<<endl; cout.clear(); LinkList L2; initList(L2); insertList(L2); listTraverse(L2);cout<<endl<<endl; //将第一个链表中从第四个结点起链接到第二个链表,构造两个相交的链表 Node *p=L; for(int i=0;i<=4;i++) { p=p->next; } Node *q=L2; while(q->next) { q=q->next; } q->next=p;//将第二个链表的尾节点 连接到L1的第5个节点中 listTraverse(L); cout<<endl<<endl; listTraverse(L2);cout<<endl<<endl; /*用p2,p2分别指向2个表头,不断后移,最后达到表尾时,p1=p2,说明有环 */ Node *p1,*p2; p1=L; p2=L2; bool isCircle=false; int count=0; while(p1->next!=NULL) p1=p1->next; while(p2->next!=NULL) p2=p2->next; if(p1==p2) { isCircle=true; } if(isCircle) cout<<"有环:"<<endl; else cout<<"没环:"<<endl; /* 求环节点 */ p1=L; p2=L2; int len1=0,len2=0,len; while(p1->next!=NULL) { p1=p1->next;len1++;} while(p2->next!=NULL) {p2=p2->next;len2++;} Node *p11=L->next,*p22=L2->next; if(p1==p2) { cout<<"有环"<<endl; if(len1>=len2) //2个链表长度的差值 { len=len1-len2; while(len--)// //遍历差值个步长 (执行abs(length1-length2)次) p11=p11->next; } else { len=len2-len1; while(len--) p22=p22->next; } while(1) { if(p11==p22)////两个链表中地址相同的结点 (最多执行的次数为:min(length1,length2)) { cout<<"第一个相交的节点:"<<p11->data; break; } else if(p11->next && p22->next) { p11=p11->next; p22=p22->next; } } }//end if else cout<<"2链表不相交"<<endl; }
输入和输出:
1 2 3 4 5 6 -1
1 2 3 4 5 6
7 8 9 -1
7 8 9
有环:
有环
第一个相交的节点:5请按任意键继续. . .
(我们故意让L2最后一个节点连接到L1的第5个节点。结果正确。
链表中含有环的问题:
2s = s + nr
s= nr
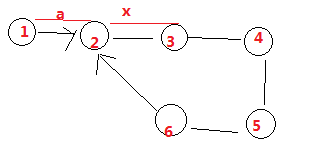
设整个链表长L,入口环与相遇点距离为x,起点到环入口点的距离为a。
a + x = nr
a + x = (n – 1)r +r = (n-1)r + L - a
a = (n-1)r + (L – a – x)
void insertList(LinkList &list) { int val; Node *tail=list; while(tail->next!=NULL) tail=tail->next; while(cin>>val && val!=-1) { Node *p=new Node(val); p->next=NULL; tail->next=p; tail=tail->next; } //人为构造环 tail->next=list->next->next->next->next;//第二个节点 } LinkList listLoop(LinkList &list) { int isLoop=0; LinkList fast,slow; fast=slow=list; while(fast && fast->next) { slow=slow->next; fast=fast->next->next;//fast每次两步,slow每次一步 if(fast==slow)////当两指针相等时,判断链表中有环 { isLoop=1; break; } } if(isLoop==1)//有环时 { slow=list; while(slow!=fast)////一个头指针,一个相遇点指针,两个第一次相等时为环入口点 { slow=slow->next; fast=fast->next; } return slow; } else { return NULL; } } int main() { LinkList L; initList(L); insertList(L); //listTraverse(L); cout<<endl<<endl; cout.clear(); Node *res=listLoop(L); if(res!=NULL) cout<<"环入口点为:"<<res->data; else cout<<"链表中没有环"<<endl; }
运行结果:
1 2 3 4 5 6 -1
环入口点为:2请按任意键继续. . .
(求环的解法:
一种比较耗空间的做法是,从头开始遍历链表,把每次访问到的结点(或其地址)存入一个集合(hashset)或字典(dictionary),如果发现某个结点已经被访问过了,就表示这个链表存在环,并且这个结点就是环的入口点。这需要O(N)空间和O(N)时间,其中N是链表中结点的数目。
如果要求只是用O(1)空间、O(N)时间,应该怎么处理呢?
其实很简单,想象一下在跑道上跑步:两个速度不同的人在操场跑道上一圈一圈地跑,他们总会有相遇的时候。因此我们只需要准备两个指针,同时从链表头出发,一个每次往前走一步,另一个每次往前走两步。如果链表没有环,那么经过一段时间,第二个(速度较快的)指针就会到达终点;但如果链表中有环,两个指针就会在环里转圈,并会在某个时刻相遇。
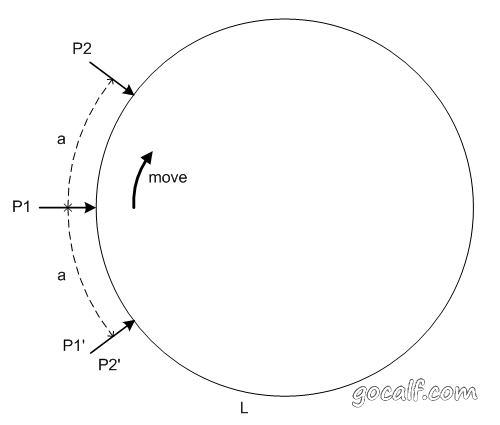
大家也许会问,这两个指针要在环里转多少圈才能相遇呢?会不会转几千几万圈都无法相遇?实际上,第一个(速度慢的)指针在环里转满一圈之前,两个指针必然相遇。不妨设环长为L,第一个指针P1第一次进入环时,第二个指针P2在P1前方第a个结点处(0 < a < L),设经过x次移动后两个指针相遇,那么应该有0+x =(a + 2x) (mod L),显然x = L-a。下面这张图可以清晰地表明这种关系,经过x = L-a次移动,P1向前移动了L-a个位置(相当于后退了a),到达P1′处,而P2向前移动了2L-2a个位置(相当于后退了2a),到达P2′处,显然P1′和P2′是同一点。
判断2个链表是否相交(没说带不带环)
1.先判断带不带环
2.如果都不带环,就判断尾节点是否相等
3.如果都带环,判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
如果在,则相交,如果不在,则不相交。
编写判断带环的代码:
struct Node { int value; Node * next; }; //1.先判断带不带环 //判断是否有环,返回bool,如果有环,返回环里的节点 //思路:用两个指针,一个指针步长为1,一个指针步长为2,判断链表是否有环 bool isCircle(Node * head, Node *& circleNode, Node *& lastNode) { Node * fast = head->next; Node * slow = head; while(fast != slow && fast && slow) { if(fast->next != NULL) fast = fast->next; if(fast->next == NULL) lastNode = fast; if(slow->next == NULL) lastNode = slow; fast = fast->next; slow = slow->next; } if(fast == slow && fast && slow) { circleNode = fast; return true; } else return false; }
综合判断2个链表是否相交的办法:
//判断带环不带环时链表是否相交 //2.如果都不带环,就判断尾节点是否相等 //3.如果都带环,判断一链表上俩指针相遇的那个节点,在不在另一条链表上。 bool detect(Node * head1, Node * head2) { Node * circleNode1; Node * circleNode2; Node * lastNode1; Node * lastNode2; bool isCircle1 = isCircle(head1,circleNode1, lastNode1); bool isCircle2 = isCircle(head2,circleNode2, lastNode2); //一个有环,一个无环 if(isCircle1 != isCircle2) return false; //两个都无环,判断最后一个节点是否相等 else if(!isCircle1 && !isCircle2) { return lastNode1 == lastNode2; } //两个都有环,判断环里的节点是否能到达另一个链表环里的节点 else { Node * temp = circleNode1->next; //updated,多谢苍狼 and hyy。 while(temp != circleNode1) { if(temp == circleNode2) return true; temp = temp->next; } return false; } return false; }
相关问题:求链表倒数第k个结点
设置两个指针p1,p2,首先p1和p2都指向head,然后p2向前走k步,这样p1和p2之间就间隔k个节点,最后p1和p2同时向前移动,直至p2走到链表末尾。
更多参考:
http://blog.csdn.net/v_july_v/article/details/6447013
http://www.360doc.com/content/12/0313/14/1429048_194005252.shtml
struct ListNode { char data; ListNode* next; }; ListNode* head,*p,*q; ListNode *pone,*ptwo; //@heyaming, 第一节,求链表倒数第k个结点应该考虑k大于链表长度的case。 ListNode* fun(ListNode *head,int k) { assert(k >= 0); pone = ptwo = head; for( ; k > 0 && ptwo != NULL; k--) ptwo=ptwo->next; if (k > 0) return NULL; while(ptwo!=NULL) { pone=pone->next; ptwo=ptwo->next; } return pone; }