题意:
给定一个(n*m)的矩阵,从中删去(k)个顶点,求最后能形成多少个正方形
范围&性质:(1le n,mle 10^6,1le kle 2000),正方形可以是斜着的(边不一定与网格图上的边重合)
分析:
(下文所有图片均来源于其他julao博客)
暴力做法:
枚举,复杂度(O(nmk)),直接去世
正解:
通过容斥简化运算,记(f(i))表示至少包含(i)个被删除的点的正方形数目,最终的答案就是(f(0)-f(1)+f(2)-f(3)+f(4)),那么问题转化成了如何求(f(i))
首先我们考虑对于一个被删除的点,它能形成的正方形有多少种,情况如下图所示
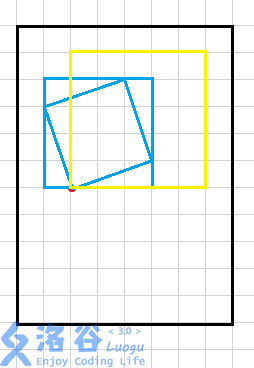
我们很容易观察出正方形可以分为两类,斜着的和正着的,但是斜着的正方形可以在大的正方形里被统计,RT
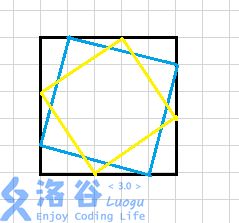
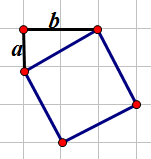
我们按照横纵坐标的差值,对斜着的正方形进行定义,如下图的正方形我们可以称其为((a,b))正方形
那么对于一个被删除的点,它的属性可以用四个值表示分别为((u,d,l,r))
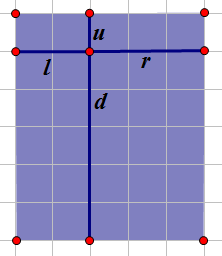
我们先考虑((0,x))正方形,也就是横平竖直的正方形,分象限考虑,这样的正方形的数目是(min(l,d)+min(d,r)+min(u,r)+min(u,l))
接下来考虑斜着的正方形,我们依旧分象限考虑,先考虑((l,r,d))所在象限,正方形((a,b))
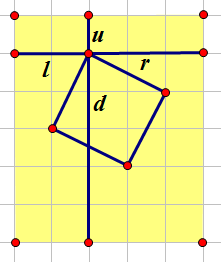
我们列出此时对(a)的限制$ale r,ale a+b-1,1le a,a+b-lle a $改为枚举a+b,转化成代码就是
for(int c=2;c<=d&&c<=l+r;c++)
{
ans+=min(r,c-1)-max(1,c-l)+1;
}
但是,单次(O(n^2))的复杂度不优秀,其实(c)影响答案的值只在([l+1,r+1])范围内,因为小于(l+1)时(min)会取1,大于$ r+1(时)min$会取r,在取值范围内是一次函数,所以可以对枚举进行优化,只枚举分界点
int lim=min(l+r,h),res=0;
int pos[3]={l+1,r+1,lim};
sort(pos,pos+3);
int cl=1,cr,vl,vr;
for(int i=0;i<3;i++)
{
cr=pos[i];
if(cr>lim) break;
if(cr<2||cl==cr) continue;
cl++;
vl=min(r,cl-1)-max(cl-l,1)+1;
vr=min(r,cr-1)-max(cr-l,1)+1;
res=(res+(vr+vl)*(cr-cl+1)/2)%mod;
cl=cr;
}
return res;
对于含两个以上的情况,枚举两个点,利用向量或者坐标等数学知识推出其他点的坐标
tip:对于含至少三个点的情况会重复计算(C_3^2)次,对于至少四个点的情况会重复计算(C_4^2)次,统计答案的时候直接除掉就可以
代码:
#include<bits/stdc++.h>
#define mk(x,y) make_pair(x,y)
using namespace std;
namespace zzc
{
const int mod = 1e8+7;
int n,m,k;
set<pair<int,int> > p;
bool check(int x,int y)
{
return x>=0&&x<=n&&y>=0&&y<=m;
}
int calc(int l,int r,int h)
{
int lim=min(l+r,h),res=0;
int pos[3]={l+1,r+1,lim};
sort(pos,pos+3);
int cl=1,cr,vl,vr;
for(int i=0;i<3;i++)
{
cr=pos[i];
if(cr>lim) break;
if(cr<2||cl==cr) continue;
cl++;
vl=min(r,cl-1)-max(cl-l,1)+1;
vr=min(r,cr-1)-max(cr-l,1)+1;
res=(res+(vr+vl)*(cr-cl+1)/2)%mod;
cl=cr;
}
return res;
}
int calc0()
{
int res=0;
for(int i=1;i<=min(n,m);i++)
{
res=(res+(long long)(m-i+1)*(n-i+1)%mod*i%mod)%mod;
}
return res;
}
int calc1()
{
int res=0;
for(set<pair<int,int> >::iterator it=p.begin();it!=p.end();it++)
{
int x=it->first,y=it->second;
res+=calc(x,n-x,y);
res+=calc(x,n-x,m-y);
res+=calc(m-y,y,x);
res+=calc(m-y,y,n-x);
res+=min(x,y);
res+=min(x,m-y);
res+=min(n-x,y);
res+=min(n-x,m-y);
res=(res+mod)%mod;
}
return res;
}
int calc2()
{
int res=0;
for(set<pair<int,int> >::iterator it=p.begin();it!=p.end();it++)
{
for(set<pair<int,int> >::iterator jt=it;jt!=p.end();jt++)
{
if(it==jt) continue;
int x1=it->first,y1=it->second,x2=jt->first,y2=jt->second;
if(check(x1+y1-y2,y1-x1+x2)&&check(x2+y1-y2,y2-x1+x2)) res++;
if(check(x1-y1+y2,y1+x1-x2)&&check(x2-y1+y2,y2+x1-x2)) res++;
if((x1+x2+y1+y2)&1) continue;
if(check((x1+x2+y1-y2)/2,(y1+y2-x2+x1)/2)&&check((x1+x2-y1+y2)/2,(y1+y2+x2-x1)/2)) res++;
}
}
return res;
}
int calc3()
{
int res=0;
for(set<pair<int,int> >::iterator it=p.begin();it!=p.end();it++)
{
for(set<pair<int,int> >::iterator jt=it;jt!=p.end();jt++)
{
if(it==jt) continue;
int x1=it->first,y1=it->second,x2=jt->first,y2=jt->second;
if(check(x1+y1-y2,y1-x1+x2)&&check(x2-y2+y1,y2+x2-x1))
{
if(p.count(mk(x1+y1-y2,y1-x1+x2))) ++res;
if(p.count(mk(x2-y2+y1,y2+x2-x1))) ++res;
}
if(check(x1-y1+y2,y1+x1-x2)&&check(x2+y2-y1,y2-x2+x1))
{
if(p.count(mk(x1-y1+y2,y1+x1-x2))) ++res;
if(p.count(mk(x2+y2-y1,y2-x2+x1))) ++res;
}
if(((y1+y2+x1+x2)&1)==0)
{
if(check((x1+x2+y2-y1)/2,(y1+y2-x2+x1)/2)&&check((x1+x2-y2+y1)/2,(y1+y2+x2-x1)/2))
{
if(p.count(mk((x1+x2+y2-y1)/2,(y1+y2-x2+x1)/2))) ++res;
if(p.count(mk((x1+x2-y2+y1)/2,(y1+y2+x2-x1)/2))) ++res;
}
}
}
}
return res/3;
}
int calc4()
{
int res=0;
for(set<pair<int,int> >::iterator it=p.begin();it!=p.end();++it)
{
for(set<pair<int,int> >::iterator jt=it;jt!=p.end();++jt)
{
if(it==jt)continue;
int x1=it->first,y1=it->second,x2=jt->first,y2=jt->second;
if(check(x1+y1-y2,y1-x1+x2)&&check(x2-y2+y1,y2+x2-x1))
{
if(p.count(mk(x1+y1-y2,y1-x1+x2)) && p.count(mk(x2-y2+y1,y2+x2-x1))) ++res;
}
if(check(x1-y1+y2,y1+x1-x2)&&check(x2+y2-y1,y2-x2+x1))
{
if(p.count(mk(x1-y1+y2,y1+x1-x2)) && p.count(mk(x2+y2-y1,y2-x2+x1))) ++res;
}
if(((y1+y2+x1+x2)&1)==0)
{
if(check((x1+x2+y2-y1)/2,(y1+y2-x2+x1)/2 && check((x1+x2-y2+y1)/2,(y1+y2+x2-x1)/2)))
{
if(p.count(mk((x1+x2+y2-y1)/2,(y1+y2-x2+x1)/2))&& p.count(mk((x1+x2-y2+y1)/2,(y1+y2+x2-x1)/2))) ++res;
}
}
}
}
return res/6;
}
void work()
{
int a,b;
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=k;i++)
{
scanf("%d%d",&a,&b);
p.insert(mk(a,b));
}
printf("%d
",(calc0()-calc1()+calc2()-calc3()+calc4()+mod)%mod);
}
}
signed main()
{
zzc::work();
return 0;
}