Poj 2528 Mayor's posters 分类： Brush Mode 2014-07-23 09:12 84人阅读 评论(0) 收藏

Mayor's posters

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 40570		Accepted: 11798

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:

• Every candidate can place exactly one poster on the wall.
  
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
  
• The wall is divided into segments and the width of each segment is one byte.
  
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed.

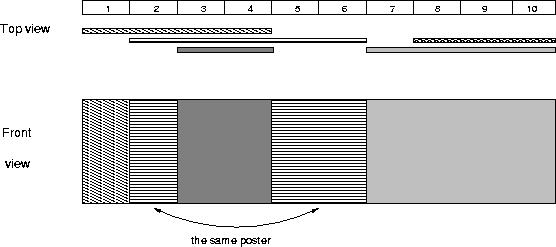
The picture below illustrates the case of the sample input.

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

题意：给n张海报能贴瓷砖的范围，问，最终可以看见多少张海报

心得：线段树的离散化的第一步，以后写线段树绝对要多建几个函数，好修改，看代码↓

#include<iostream>
#include<cstdio>
#include<cstring>
#include <algorithm> 
#define Max 10005
using namespace std;
struct node{
	int l, r, m, s;
}Tree[Max<<3];
int li[Max], ri[Max];
int point[Max<<2];
int see[Max];
int ans;
int n, m, ni;

void Complex(){
	memset(li,0,sizeof(li));
	memset(ri,0,sizeof(ri));
	memset(point,0,sizeof(point));
	memset(see,0,sizeof(see));
}

void Build(int l,int r,int k)
{
	Tree[k].l = l;
	Tree[k].r = r;
	Tree[k].s = -1;
	Tree[k].m = (l+r)>>1;
	if(l==r)	return;
	Build(Tree[k].m+1,r,k+k+1);
	Build(l,Tree[k].m,k+k);
	return;
}

void update(int l, int r, int k)
{
	if(Tree[k].l == l && Tree[k].r == r)
	{
		Tree[k].s = ni;	
		return;
	}		
	else if(Tree[k].s != -1)
	{
		Tree[k+k].s = Tree[k+k+1].s = Tree[k].s;
		Tree[k].s = -1;
	}	
	
	if(r <= Tree[k].m)	update(l, r, k+k);
	else if(l > Tree[k].m)	update(l, r, k+k+1);
	else
	{
		update(l, Tree[k].m, k+k);
		update(Tree[k].m + 1, r, k+k+1);
	}
	return;
}

void Query(int k)		//统计 
{
	if(Tree[k].s>=0)
	{
		if(!see[Tree[k].s]++)		ans++;
		return;
	}
	Query(k+k);
	Query(k+k+1);
	return;
}

int Bin(int xi)			//二分查找特定点在关键点数字中的位置，为了更新线段树 
{
	int l = 1, r = m;
	while(l<=r)
	{
		int mi = (l+r)>>1;
		if(xi == point[mi])		return mi;
		if(xi >= point[mi])		l = mi + 1;
		else	r = mi - 1;
	}
	return -1;
}

void Myscanf()			//统一输入，方便修改 
{
	ans = 0;
	m = 1;
	scanf("%d",&n);
	for(int i=0; i<n; i++)
	{
		scanf("%d%d",&li[i],&ri[i]);
		point[m++] = li[i];
		point[m++] = ri[i];
	}
}

void Point_Do()				//先排序在去重，达到离散的效果 
{
	int mi = 0;
	sort(point+1,point+1+m);
	for(int i=1; i<=m; i++)
	{
		if(point[i]!=point[mi])		point[++mi] = point[i]; 		//去重
	}		
	m = mi;
}

void Find_Point()
{
	for(int i=0; i<n; i++)
	{
		ni = i;
		update(Bin(li[i]),Bin(ri[i]),1);
	}
}

int main()
{
	int num;
	scanf("%d",&num);
	while(num--)
	{
		Complex();			//初始化函数 
		Myscanf();			//输入函数 
		Point_Do();			//处理关键点函数 
		Build(1,m,1);		//建树函数 
		Find_Point();		//对各个海报范围的处理函数 
		Query(1);			//统计函数 
		printf("%d
",ans);			//输出结果 
	}	

	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。