解法示意
- 需借助二进制
- 不妨以四层塔为例走一个
- 我把左、中、右三根柱子依次称为 A, B, C
- 金片默认都在 A 塔
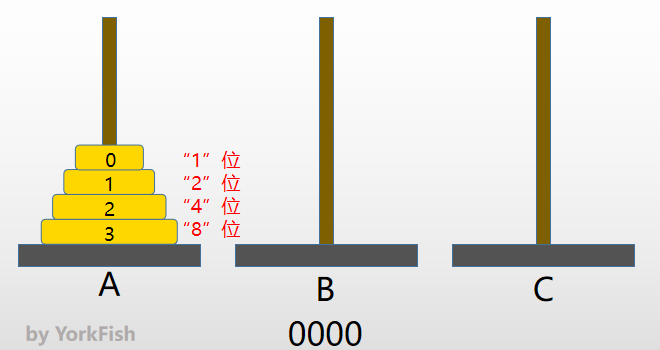
n片金片从小到大依次编号为0,1,2, ...n-1- 设初始值为 0000(2)
- 按
8,4,2,1称呼二进制的各位,对应关系如下图所示
step1
- 开始累加,每次加一
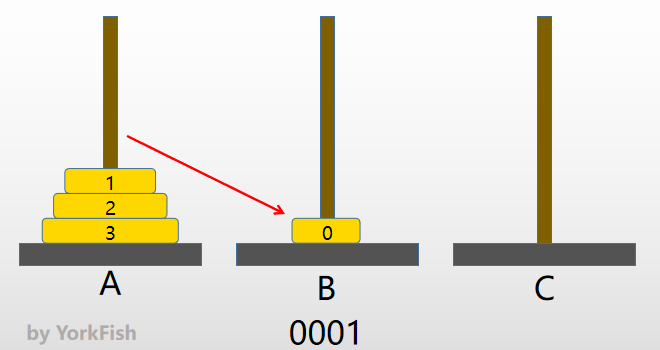
- 0000(2) => 0001(2)
- 因为1位由
0变1,所以将0号金片右移,即将0号金片由 A 移至 B - 补充:若要将 C 上的金片右移,则移至 A,因为三个塔是循环的
step2
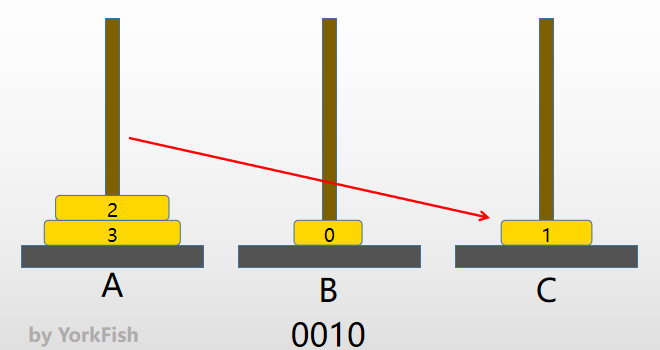
- 0001(2) => 0010(2)
- 产生进位,进到哪位,就移动该位对应的金片
- 因为进位至2位,所以将
1号金片右移 - 因为
1号金片不能放到 B,所以继续向右走,C 正好符合要求
step3
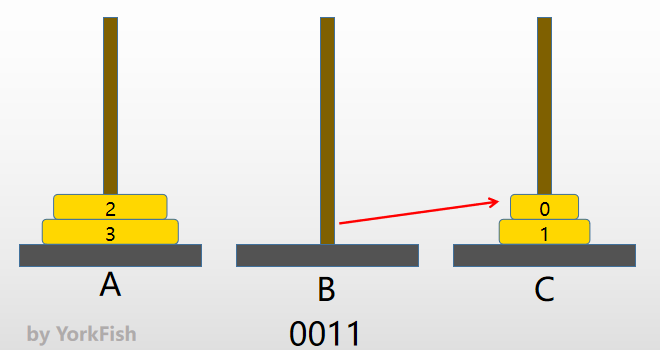
- 0010(2) => 0011(2)
- 因为1位由
0变1,所以将0号金片右移,即将0号金片由 B 移至 C
step4
- 0011(2) => 0100(2)
- 产生进位,因为进至4位,所以将
2号金片右移

step5
- 0100(2) => 0101(2)
- 因为1位由
0变1,所以将0号金片右移,即将0号金片由 C 移至 A
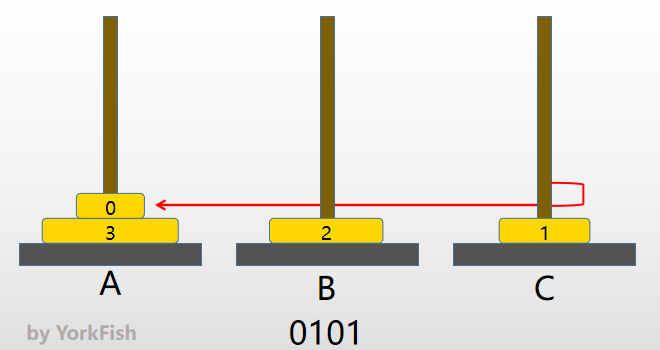
- 按这个方法进行下去,当数字变成
1111时,A 塔的四片金片就都在 C 塔上了
说明
关于结果
- 此“二进制”方法可行,但奇数金片与偶数金片在结果上有些许不同
- 若金片总数为奇数,最终会移至 B 塔
- 若金片总数为偶数,最终会移至 C 塔
- 使用高数中“轮换对称性”,在遇到奇数金片时,把原来的 B 塔看成 C 塔,把原来的 C 塔看成 B 塔
两个规律
- 规律一
- 因为每走一步,数值加一,所以该二进制数即为步数
- 该二进制数末尾
0的个数对应要移动的金片- 没有 0,即为 0 个 0,对应
0号金片;可回顾图0001,0011,0101 - 1 个 0,对应
1号金片;可回顾图0010 - 2 个 0,对应
2号金片;可回顾图0100 - 依此类推
- 没有 0,即为 0 个 0,对应
- 规律二
- 编号为
0,2,4, ... 的金片,总是进行右移操作 - 编号为
1,3,5, ... 的金片,总是进行左移操作- 因为只有三根柱子,所以右移 2 格就是左移 1 格
- 编号为
移动次数
-
按递归的思路,汉诺塔可分成三大步
- 将 A 上 n-1 片金片移至 B
- 将 A 剩余的 1 片金片移至 C
- 将 B 的 n-1 片金片移至 C
-
设
f(n)为n片金片完成移动需要的最少次数,则f(n) = f(n-1) + 1 + f(n-1),即f(n) = 2f(n-1) + 1- 若只有 1 片金片,则
f(1) = 1 - 若有 2 片金片,则
f(2) = 3 - 若有 3 片金片,则
f(3) = 7 - 照此规律,可假设
f(n) = 2^n - 1
- 若只有 1 片金片,则
-
可以用“第一类数学归纳法”证明
f(n) = 2^n - 1- 当
n = 1时,f(1) = 2^1 - 1 = 1,成立 - 当
n = k时,设f(k) = 2^k - 1成立 - => 当
n = k + 1时,f(k+1) = 2f(k) + 1 = 2 * (2^k - 1) + 1 = 2^(k+1) - 1,满足假设 - => 汉诺塔的移动次数为
f(n) = 2^n - 1,证毕
- 当
代码
def hanoi(n):
cols = ['A', 'B', 'C'] if n % 2 == 0 else ['A', 'C', 'B']
golds = [0] * n # golds[idx] == tower_idx
for step in range(1, 2 ** n):
idx = len(bin(step & -step)) - 3 # lowbit 转二进制,开头是 0b1
old_tower = cols[golds[idx]]
golds[idx] = (golds[idx] + 1 + idx % 2) % 3 # 奇数比偶数多走一步
print(f"step{step}: 将{idx}号金片从{old_tower}移到{cols[golds[idx]]}")