最短Hamilton路径（状态压缩DP）

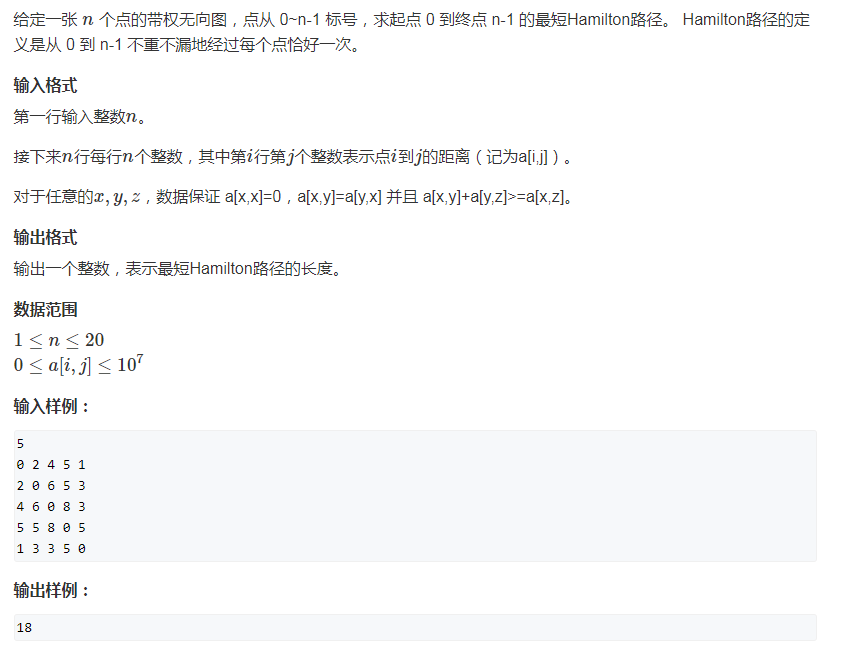
 分析：

　　　　　首先我们要思考如果让这个NP完全题目复杂度降低，那么可以优先考虑到使用位运算，状态压缩等解决思路。

　　　　然后接着思考，我们可以发现，我们所需要的不是整个方案，而只是方案最优解，所以我们只需要记录当前这个方案的最优解即可，那么我们考虑的状态，不久只有，在当前方案i中，目前抵达的点是j。
　　　　现在既然装填已经确定好了当前点j，那么这个j点是由哪一个状态移动而来的呢？我们可以选择k，也就是说我们的状态转移方程可以为
　　　　　　f[i][j]=min(f[i][j],f[i^(1<<j)][k]+w[k][j]

　　　　以上转移方程，w数组为权值 ，也就是w[k][j]是k点到j点的权值
　　　　i^(1<<j)的意思是，i 异或 1右移j位，具体来说就是i这个方案集合 xor 10……0,(其中1的位置在第j位)。
　　　　那么这个位运算有什么用处呢，第一点它是在判断第j位的情况，第二点位运算处理速度很快。

import java.util.*;
class Main {
    
    public static void main(String[] args) {
        
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[][] w = new int[n][n];
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) {
                w[i][j] = sc.nextInt();
            }
        }
        int[][] f = new int[1<<n][n];
        for(int[] d : f) Arrays.fill(d,Integer.MAX_VALUE / 2);
        f[1][0] = 0;
        for(int i = 0; i < 1 << n; i++) {
            for(int j = 0; j < n; j++) {
                if(((i >> j) & 1) != 0) {
                    for(int k = 0; k < n; k++) {
                        if((((i - (1 << j)) >> k) & 1) != 0) {
                            f[i][j] = Math.min(f[i][j],f[i-(1<<j)][k] + w[k][j]);
                        }
                    }
                }
            }
        }
        System.out.print(f[(1<<n)-1][n-1]);
    }
}

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 20, M = 1 << N;

int n;
int f[M][N];
int w[N][N];


int main() {
    cin >> n;
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            cin >> w[i][j];
        }
    }
    memset(f,0x3f,sizeof f);
    f[1][0] = 0;
    for(int i = 0; i < 1 << n; i++) {
        for(int j = 0; j < n; j++) {
            if(i>>j&1) {
                for(int k = 0; k < n; k++) {
                    if((i-(1 << j)) >> k & 1) {
                        f[i][j] = min(f[i][j],f[i-(1 << j)][k] + w[k][j]);
                    }
                }
            }
        }
    }
    cout << f[(1 << n) - 1][n-1];
    return 0;
}