任意门:http://poj.org/problem?id=1470
Closest Common Ancestors
| Time Limit: 2000MS | Memory Limit: 10000K | |
| Total Submissions: 22519 | Accepted: 7137 |
Description
Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)
Input
The data set, which is read from a the std input, starts with the tree description, in the form:
nr_of_vertices
vertex:(nr_of_successors) successor1 successor2 ... successorn
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
nr_of_pairs
(u v) (x y) ...
The input file contents several data sets (at least one).
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.
nr_of_vertices
vertex:(nr_of_successors) successor1 successor2 ... successorn
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
nr_of_pairs
(u v) (x y) ...
The input file contents several data sets (at least one).
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.
Output
For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times
For example, for the following tree:
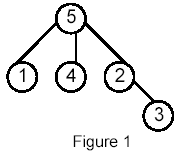
For example, for the following tree:

Sample Input
5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
(2 3)
(1 3) (4 3)
Sample Output
2:1 5:5
Hint
Huge input, scanf is recommended.
题意概括:
给一棵 N 个结点 N-1 条边的树,和 M 次查询;
形式是:先给根结点 然后 给与这个根结点相连的 子节点。
查询的对儿给得有点放荡不羁,需要处理一下空格、回车、括号。。。
解题思路:
虽说表面上看是一道裸得 LCA 模板题(简单粗暴Tarjan)
但是细节还是要注意:
本题没有给 查询数 M 的范围(RE了两次)所以要投机取巧一下不使用记录每对查询的 LCA。
本题是多测试样例,注意初始化!!!
AC code:
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 #include <vector> 6 #define INF 0x3f3f3f3f 7 #define LL long long 8 using namespace std; 9 const int MAXN = 1e3+10; 10 struct Edge{int v, w, nxt;}edge[MAXN<<1]; 11 struct Query 12 { 13 int v, id; 14 Query(){}; 15 Query(int _v, int _id):v(_v), id(_id){}; 16 }; 17 vector<Query> q[MAXN]; 18 19 int head[MAXN], cnt; 20 int fa[MAXN], ans[MAXN<<1], no[MAXN]; 21 bool vis[MAXN], in[MAXN]; 22 int N, M; 23 24 void init() 25 { 26 memset(head, -1, sizeof(head)); 27 memset(in, false, sizeof(in)); 28 memset(vis, false, sizeof(vis)); 29 //memset(ans, 0, sizeof(ans)); 30 memset(no, 0, sizeof(no)); 31 cnt = 0; 32 for(int i = 0; i <= N; i++) 33 fa[i] = i, q[i].clear(); 34 } 35 36 int getfa(int x){return fa[x]==x?x:fa[x]=getfa(fa[x]);} 37 38 void AddEdge(int from, int to) 39 { 40 edge[cnt].v = to; 41 edge[cnt].nxt = head[from]; 42 head[from] = cnt++; 43 } 44 45 void Tarjan(int s, int f) 46 { 47 int root = s; 48 fa[s] = s; 49 for(int i = head[s]; i != -1; i = edge[i].nxt) 50 { 51 int Eiv = edge[i].v; 52 if(Eiv == f) continue; 53 Tarjan(Eiv, s); 54 fa[getfa(Eiv)] = s; 55 } 56 vis[s] = true; 57 for(int i = 0; i < q[s].size(); i++){ 58 //if(vis[q[s][i].v]) ans[q[s][i].id] = getfa(q[s][i].v); 59 if(vis[q[s][i].v]) 60 no[getfa(q[s][i].v)]++; 61 } 62 } 63 64 int main() 65 { 66 while(~scanf("%d", &N)){ 67 init(); 68 //scanf("%d", &N); 69 for(int i = 1, u, v, k; i <= N; i++){ 70 scanf("%d:(%d)", &u, &k); 71 for(int j = 1; j <= k; j++){ 72 scanf("%d", &v); 73 AddEdge(u, v); 74 in[v] = true; 75 } 76 } 77 int root = 0; 78 for(int i = 1; i <= N; i++) if(!in[i]){root = i;break;} 79 scanf("%d", &M); 80 int sum = 1, u, v; 81 while(sum <= M){ 82 while(getchar()!='('); 83 scanf("%d%d", &u, &v); 84 while(getchar()!=')'); 85 q[u].push_back(Query(v, sum)); 86 q[v].push_back(Query(u, sum)); 87 sum++; 88 } 89 Tarjan(root, -1); 90 /* 91 for(int i = 1; i <= M; i++){ 92 no[ans[i]]++; 93 } 94 */ 95 96 for(int i = 1; i <= N; i++){ 97 if(no[i]) printf("%d:%d ", i, no[i]); 98 } 99 } 100 return 0; 101 }