任意门:http://codeforces.com/contest/689/problem/E
E. Mike and Geometry Problem
Mike wants to prepare for IMO but he doesn't know geometry, so his teacher gave him an interesting geometry problem. Let's define f([l, r]) = r - l + 1 to be the number of integer points in the segment [l, r] with l ≤ r (say that 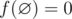 ). You are given two integers nand k and n closed intervals [li, ri] on OX axis and you have to find:
). You are given two integers nand k and n closed intervals [li, ri] on OX axis and you have to find:

In other words, you should find the sum of the number of integer points in the intersection of any k of the segments.
As the answer may be very large, output it modulo 1000000007 (109 + 7).
Mike can't solve this problem so he needs your help. You will help him, won't you?
The first line contains two integers n and k (1 ≤ k ≤ n ≤ 200 000) — the number of segments and the number of segments in intersection groups respectively.
Then n lines follow, the i-th line contains two integers li, ri ( - 109 ≤ li ≤ ri ≤ 109), describing i-th segment bounds.
Print one integer number — the answer to Mike's problem modulo 1000000007 (109 + 7) in the only line.
3 2
1 2
1 3
2 3
5
3 3
1 3
1 3
1 3
3
3 1
1 2
2 3
3 4
6
In the first example:
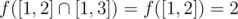 ;
;
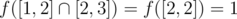 ;
;
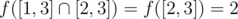 .
.
So the answer is 2 + 1 + 2 = 5.
大概题意:
有 N 个区间, 从其中取 K 个区间。所以有 C(N, K)种组合, 求每种组合区间交集长度的总和。
解题思路:
丢开区间的角度,从每个结点的角度来看,其实每个结点的贡献是 C(cnt, K) cnt 为该结点出现的次数, 所以只要O(N)扫一遍统计每个结点的贡献就是答案。
思路清晰,但考虑到数据的规模,这里需要注意和需要用到两个技巧:
一是离散化,这里STL里的 vector 和 pair 结合用,结合区间加法的思想进行离散化。
二是求组合数时 除数太大,考虑到精度问题需要用逆元来计算。
AC code:

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn = 2e5+7; 4 const int mod = 1e9+7; 5 long long fac[maxn]; 6 7 long long qpow(long long a,long long b) //快速幂 8 { 9 long long ans=1;a%=mod; 10 for(long long i=b;i;i>>=1,a=a*a%mod) 11 if(i&1)ans=ans*a%mod; 12 return ans; 13 } 14 15 long long C(long long n,long long m) //计算组合数 16 { 17 if(m>n||m<0)return 0; 18 long long s1=fac[n], s2=fac[n-m]*fac[m]%mod; //除数太大,逆元处理 19 return s1*qpow(s2,mod-2)%mod; 20 } 21 int n,k; 22 int l[maxn],r[maxn]; //左端点, 右端点 23 int main() 24 { 25 fac[0]=1; 26 for(int i=1;i<maxn;i++) //预处理全排列 27 fac[i]=fac[i-1]*i%mod; 28 29 scanf("%d%d",&n,&k); 30 for(int i=1;i<=n;i++){ 31 scanf("%d",&l[i]); 32 scanf("%d",&r[i]); 33 } 34 vector<pair<int,int> >op; 35 for(int i=1;i<=n;i++){ //离散化 36 op.push_back(make_pair(l[i]-1,1)); //区间加法标记 37 op.push_back(make_pair(r[i],-1)); 38 } 39 sort(op.begin(),op.end()); //升序排序 40 long long ans = 0; //初始化 41 int cnt=0; 42 int la=-2e9; 43 for(int i=0;i<op.size();i++){ //计算每点的贡献 44 ans=(ans+C(cnt,k)*(op[i].first-la))%mod; 45 la=op[i].first; 46 cnt+=op[i].second; //该点的前缀和就是该点的出现次数 47 } 48 cout<<ans<<endl; 49 }
