R语言基础 | 概率分布的表示方法

在R中各种概率函数都有统一的形式，即一套统一的 前缀+分布函数名(参数)：

分布函数

注意：不同前缀，第一个参数 n 的意义不同（详见下方讲解）

连续型

名称	英文名	R对应的函数	参数
高斯分布	gaussian	norm	n, mean=0, sd=1
指数分布	exponential	exp	n, rate=1
伽玛分布(γ)	gamma	gamma	n, shape, scale=1
韦氏分布	Weibull	weibull	n, shape, scale=1
柯西分布	Cauchy	cauchy	n, location=0, scale=1
β分布	beta	beta	n, shape1, shape2
t分布	Student's t	t	n, df
F分布	F	f	n, df1, df2
卡方分布	chi-squared	chisq	n, df
Logistic 分布	Logistic	logis	n, location=0, scale=1
对数正态分布	log-normal	lnorm	n, meanlog=0, sdlog=1
均匀分布	uniform	unif	n, min=0, max=1

离散型

名称	英文名	R对应的函数	参数
泊松分布	Poisson	pois	n, lambda
二项分布	binomail	binom	n, size, prob
多项分布	multinomial	multinom	n, size, prob
几何分布	geometric	geom	n, prob
超几何分布	hypergeometric	hyper	nn, m, n, k
负二项分布	negative binomial	nbinom	n, size, prob

前缀

　　r：随机函数，生成特定分布的随机数（random）   

　　d：密度函数（density）

  p：分布函数（生成相应分布的累积概率密度函数）

  q：分位数函数，能够返回特定分布的分位数（quantile）

代码示例

以 正态分布 为例

1. r 生成正态分布的随机数

第一个参数 n：生成随机数的个数

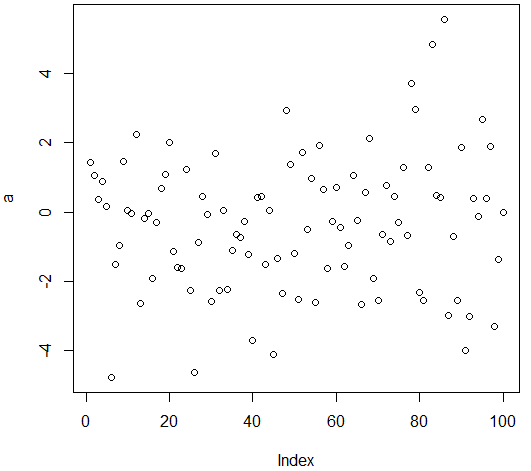
a = rnorm(100,0,2)  # 生成100个均值为0，标准差为2 的呈正态分布的点

plot(a)   # 在图上展示这些点，x轴:索引 y轴:点的数值

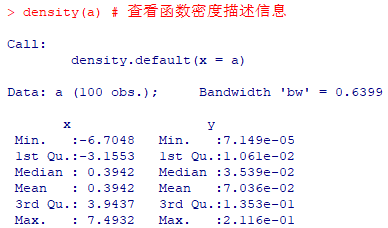
density(a) # 查看函数密度描述信息

hist(a)  # 直方图呈现

 查看概率密度图

hist(a, xlab="值", ylab="频次",xlim=c(-8,8),ylim=c(0,0.3))
lines(density(a), col="blue")

2.  d 密度函数

第一个参数 n：x 值

dnorm(0.2, 0, 2) # 计算x=0.2 处 函数的概率密度，得到一个数值

 3. p 分布函数

第一个参数 n：x 值

pnorm(0.2, 0, 2) # 计算x=0.2 处 累积概率密度函数值 即 x 小于 0.2 的概率（相当与对应的百分位数）

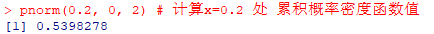
 4. q 分位数函数 

第一个参数 n：分位数值

qnorm(0.25, 0, 2)  # 计算下四分位数 所对应的正态分布中的那个数据