创建一维数组:
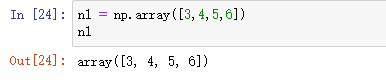
创建二维数组:

查看数组形状:
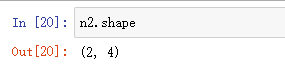
参数为列表的创建方法:
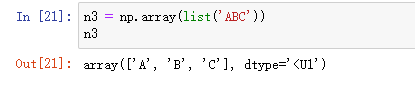
创建一个10*8的全为1的矩阵:

创建4*4全为0的矩阵:
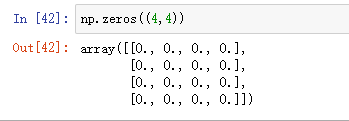
填充矩阵:

创建满秩矩阵:
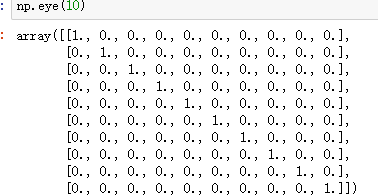
平均分组:(0-100)
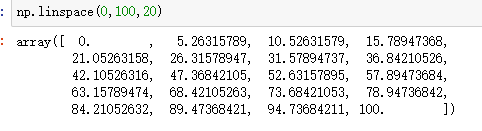
迭代器生成数组,左闭右开:步长为2的数组

随机生成一个一维数组,5个元素:
np.random.ranint(0,150,size=5)
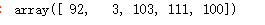
返回100个标准正太分布的样本:

自定义一个正太分布数组:
均值为175,标准差1,维度100(一维)

矩阵加法:

或者
np.add(n,n)
减,乘,除 同理。
乘法:m*n的矩阵必须 对应n*m的矩阵。
np.dot(n1,n2)

广播机制:
在加法运算过程中,如果一方出现缺失值,会自动填充已有值。

高效冒泡排序:
n3 = np.array([3,4,2,6,56,112,23,1])
n3
def sortnd(nd):
for i in range(nd.size):
min_index = np.argmin(nd[i:])+i
nd[i],nd[min_index] = nd[min_index],nd[i]
return n3
sortnd(n3)
n1.sort()和np.sort(n1)的区别:
前者就地排序。不占用内存,后者生成新数组,不影响原数组。

np.partition(nd,k) 当k<0时 按从大到小排列最大的K项放在末尾,k>0时相反。取最小的几位放在前面。
求四维数组最后两项的和:

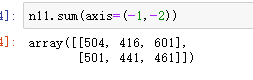
重新定形:
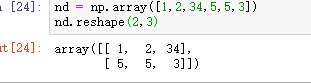
矩阵级联:np.concatenate()
竖直级联

水平级联:np.concatenate(n6,n6,axis=1)
被连接的数组一定不能是一维数组 axis<数组维度

竖直折叠矩阵:
np.vstack()

水平平铺矩阵,(降一次维)

矩阵切割:
np.split(n5,(1,3),axis =1) 竖直切 axis=0时,水平切。
第二种
np.vsplit() 水平切
np.hsplit() 竖直切
最大值():
nd.max( axis=0) axis =0/1/2 ------> 维度
np.mean(nd,axis=0) 均值
np.sum(nd,axis =0 ) 求和
返回最值索引:
np,argmax(nd)
np.argmin(nd)
条件过滤:
index = np.argwhere(n>50)
n[index]