注:题解来自左程云大佬,记录一下
这个问题可以看做是 算法练习(7)-判断单链表是否有环,以及求环的长度 的升级版,分析:对于单链表而言,如果2个链表能相交,只可能出现下面这几种情况
| 链表1 类型 | 链表2 类型 | 相交可能性? | 备注 | 图例 |
| 无环 | 无环 | √ | 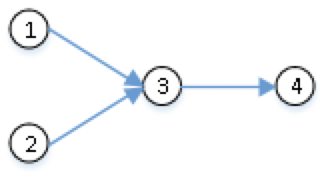 |
|
| 无环 | 有环 | × | 如果能相交,必然2个都是有环 | |
| 有环 | 有环 | √ | 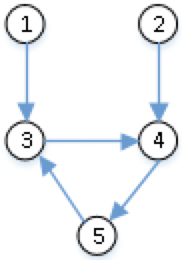 或 或 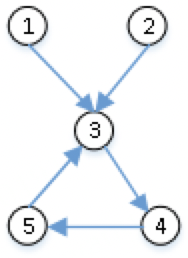 |
可以分解成几个小问题:
1、如何判断链表是有环的?
/**
* 如果1个单链表有环,返回入环节点
*
* @param head
* @return 如果有环, 则返回入环节点,否则返回null
*/
public static LinkNode getLoopEntrance(LinkNode head) {
if (head == null || head.next == null) {
return null;
}
LinkNode slow = head;
LinkNode fast = head;
boolean isLoop = false;
//先跑一圈, 判断是否有环
while (fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow.equals(fast)) {
isLoop = true;
break;
}
}
if (!isLoop) {
return null;
}
//快指针重回头部,再跟慢指针齐步向前走,fast与slow必然相交于入环点(数学上可证明,证明过程略)
fast = head;
while (fast.next != null) {
if (slow.equals(fast)) {
return slow;
}
slow = slow.next;
fast = fast.next;
}
return null;
}
2、如何判断2个无环链表,是否相交?
/**
* 返回2个无环链表的相交节点
*
* @param head1 链表1的头节点
* @param head2 链表2的头节点
* @return 如果相交,则返回相交节点,否则返回null
*/
public static LinkNode getNoLoopCrossNode(LinkNode head1, LinkNode head2) {
//思路:先测量各自的长度, 然后找出长度差值
//第二轮遍历时, 让长度大的链表先走差值步,再2个链表齐步走, 如果有相交,必然在交叉点相遇
if (head1 == null || head2 == null) {
return null;
}
int size1 = 0, size2 = 0;
LinkNode h1 = head1, h2 = head2;
while (h1 != null) {
size1 += 1;
h1 = h1.next;
}
while (h2 != null) {
size2 += 1;
h2 = h2.next;
}
int diff = Math.abs(size1 - size2);
//让h1指向长的链表头
h1 = size1 >= size2 ? head1 : head2;
//让h2指向短的链表头
h2 = h1.equals(head2) ? head1 : head2;
//长链表先走差值步
for (int i = 0; i < diff; i++) {
h1 = h1.next;
}
//2个链表再齐步走
while (h1 != null && h2 != null) {
if (h1.equals(h2)) {
return h1;
}
h1 = h1.next;
h2 = h2.next;
}
return null;
}
3、如何判断2个有环链表,是否相交?
/**
* 判断2个有环单链表是否相交
*
* @param entrance1 链表1的入环节点
* @param entrance2 链表2的入环节点
* @return 如果相交, 返回相交点
*/
public static LinkNode getLoopCrossNode(LinkNode entrance1, LinkNode entrance2) {
if (entrance1 == null || entrance2 == null) {
return null;
}
//2个入环节点相同, 必然相交
if (entrance1.equals(entrance2)) {
return entrance1;
}
//从入环节点a出发, 一直向前走, 直到再次遇到自己前, 如果路上遇到另1个入环节点b,则a,b肯定在一个环上
LinkNode n1 = entrance1;
while (entrance1 != null) {
if (entrance1.equals(entrance2)) {
return entrance1;
}
entrance1 = entrance1.next;
if (n1.equals(entrance1)) {
break;
}
}
return null;
}
综合以上几个小方法, 就能解决该问题:
/**
* 如果2个(可能有环的)链表相交,返回相交点
* @param h1 链表1的头节点
* @param h2 链表2的头节点
* @return 如果相交,返回相交节点
*/
public static LinkNode getCrossNode(LinkNode h1, LinkNode h2) {
LinkNode entrance1 = getLoopEntrance(h1);
LinkNode entrance2 = getLoopEntrance(h2);
if (entrance1 == null && entrance2 == null) {
//都是无环链表
return getNoLoopCrossNode(h1, h2);
}
//至少1个是有环链表
return getLoopCrossNode(entrance1, entrance2);
}