2019qbxtCSP-S2 模拟题1

T1

(solution)

求出第一个开始下降的位置，移动到连续的与它相同的数的最前面的一个数的位置，记录为(p)

(p)以前的位置的数与原数相同，(p)位置为原数-1，后面全部为9

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

const int MAXN=200010;

int n,a[MAXN],ans[MAXN];
char s[MAXN];

int main()
{
	freopen("increase.in","r",stdin);
	freopen("increase.out","w",stdout);
	scanf("%s",s+1);
	n=strlen(s+1);
	for(int i=1;i<=n;++i)
		a[i]=s[i]-'0';
	int pos=n+1;
	for(int i=1;i<n;++i)
		if(a[i]>a[i+1]){
			pos=i;
			break;
		}
	if(pos<n)
		while(pos>1&&a[pos-1]==a[pos]) --pos;
	for(int i=1;i<=n;++i){
		if(i<pos) ans[i]=a[i];
		else if(i==pos) ans[i]=a[i]-1;
		else ans[i]=9;
	}
	int i=1;
	while(ans[i]==0&&i<n) ++i;
	for(;i<=n;++i)
		printf("%d",ans[i]);
	puts("");
	fclose(stdin); fclose(stdout);
	return 0;
}

T2

(solution)

考虑每一对逆序对的贡献为$a[i] imes a[j] imes i imes (n-j+1) $

用树状数组维护满足a[i]>a[j]的$ sum{ a[j] imes (n-j+1)} $即可

也可以在归并排序时记录一个后缀和处理

需要龟速乘法防止爆long long

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#define int long long
using namespace std;

const int MAXN=100010;
const int MOD=1000000000007ll;

inline int read(){
	int x=0,f=1; char c=getchar();
	while(c<'0'){ if(c=='-') f=-1; c=getchar(); }
	while(c>='0') x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}

inline int mul(int x,int y){
	int s=0ll;
	while(y){
		if(y&1) s=(s+x)%MOD;
		y>>=1ll;
		x=(x+x)%MOD;
	}
	return s;
}

int n,Ans;
struct Data{
	int v,id,nv;
} a[MAXN];

inline bool cmp1(Data x,Data y){
	return x.v<y.v;
}

inline bool cmp2(Data x,Data y){
	return x.id<y.id;
}

int tree[MAXN];
inline int lowbit(int x){ return x&(-x); }
inline int query(int x){
	int ans=0;
	for(;x;x-=lowbit(x))
		ans=(ans+tree[x])%MOD;
	return ans;
}
inline void update(int x,int d){
	for(;x<=n;x+=lowbit(x))
		tree[x]=(tree[x]+d)%MOD;
}

signed main()
{
	freopen("multiplication.in","r",stdin);
	freopen("multiplication.out","w",stdout);
	scanf("%lld",&n);
	if(n<=1000){
		for(int i=1;i<=n;++i)
			a[i].v=read();
		int tmp1,tmp2;
		for(int i=1;i<n;++i)
			for(int j=i+1;j<=n;++j)
				if(a[i].v>a[j].v){
					tmp1=mul(a[i].v,a[j].v);
					tmp2=mul(i,n-j+1);
					Ans=(Ans+mul(tmp1,tmp2))%MOD;
				}
		printf("%lld
",(Ans+MOD)%MOD);
	}
	else{
		for(int i=1;i<=n;++i)
			a[i].v=read(),a[i].id=i;
		sort(a+1,a+1+n,cmp1);
		int cnt=0; a[0].v=-1;
		for(int i=1;i<=n;++i)
			a[i].nv=(a[i].v==a[i-1].v)?cnt:++cnt;
		sort(a+1,a+1+n,cmp2);
		for(int i=n;i>=1;--i){
			Ans=(Ans+mul(mul(a[i].v,i),query(a[i].nv-1)))%MOD;
			int d=mul(a[i].v,n-i+1);
			update(a[i].nv,d);
		}
		printf("%lld
",(Ans+MOD)%MOD);
	}
	fclose(stdin); fclose(stdout);
	return 0;
}
/*
5
3 2 1 5 4
125
6
1000 2 400 6 1 400
9
100000 23333 19260817 19491001 2897370649 1 32 114514 1919810
78834965239
*/

T3

(solution1)

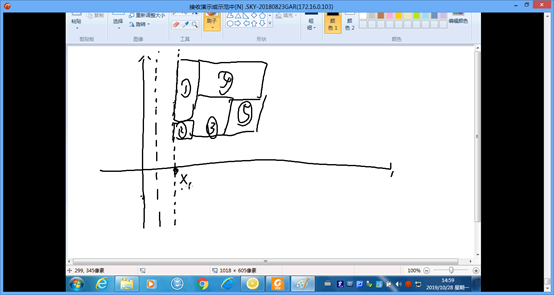
先检查各个小正方形的面积和是否等于大正方形，

之后只要满足不重叠就可以了

扫描线线段树维护，在区间加入覆盖标记前判断是否已经被覆盖

(solution2)

先检查面积，再判重叠

考察一个图中的每一个点，不难发现，以每个点为原点，每个点的四个象限都必须有且只有一个矩形覆盖

于是对每个点维护四个标记，对于边、角特殊处理，每个矩形的对四个角上的点的对应象限打标记即可

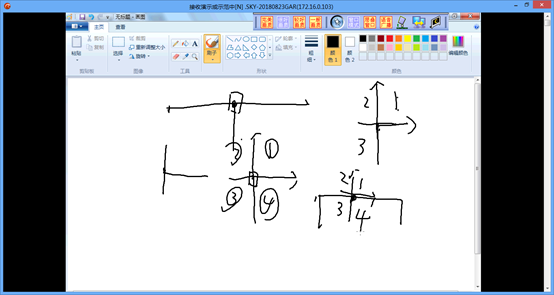
简化：内部的一个点只能成为2个或4个矩形的顶点，直接记录判断即可

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>

using namespace std;

#define INF 2147483647
#define maxn 100010

int n,rectangles[maxn][4];

struct point
{
	int x,y,d;
	point(){}
	point(int a,int b,int c)
	{
		x=a;y=b;d=c;
	}
}p[maxn<<2],q[maxn<<2];

bool operator<(const point &a,const point &b)
{
	if (a.x!=b.x) return a.x<b.x;
	return a.y<b.y;
}

bool cmp(const point &a,const point &b)
{
	if (a.y!=b.y) return a.y<b.y;
	return a.x<b.x;
}

struct line
{
	int x,y,l,r,d;
	line(){}
	line(int a,int b,int c,int e)
	{
		x=a;y=a;l=b;r=c;d=e;
	}
}vert[maxn<<2],hori[maxn<<2];

bool operator<(const line &a,const line &b)
{
	if (a.x!=b.x) return a.x<b.x;
	if (a.l!=b.l) return a.l<b.l;
	return a.r<b.r;
}

bool isRectangleCover() {
	int minx=INF,maxx=-INF,miny=INF,maxy=-INF;
	for (int a=0;a<n;a++)
	{
		minx = min(minx,rectangles[a][0]);
		maxx = max(maxx,rectangles[a][2]);
		miny = min(miny,rectangles[a][1]);
		maxy = max(maxy,rectangles[a][3]);
	}
	long long s=(0ll+maxx-minx)*(0ll+maxy-miny);
	for (int a=0;a<n;a++)
		s -= (0ll+rectangles[a][2]-rectangles[a][0])*(0ll+rectangles[a][3]-rectangles[a][1]);
	if (s) return false;
	int m=0,n1=0,n2=0;
	for (int a=0;a<n;a++)
	{
		p[++m]=point(rectangles[a][0],rectangles[a][1],1);
		p[++m]=point(rectangles[a][2],rectangles[a][1],2);
		p[++m]=point(rectangles[a][2],rectangles[a][3],4);
		p[++m]=point(rectangles[a][0],rectangles[a][3],8);
		vert[++n1]=line(rectangles[a][1],rectangles[a][0],rectangles[a][2],3);
		vert[++n1]=line(rectangles[a][3],rectangles[a][0],rectangles[a][2],12);
		hori[++n2]=line(rectangles[a][0],rectangles[a][1],rectangles[a][3],9);
		hori[++n2]=line(rectangles[a][2],rectangles[a][1],rectangles[a][3],6);
	}
	sort(p+1,p+m+1);
	sort(vert+1,vert+n1+1);
	sort(hori+1,hori+n2+1);
	int k=0;
	for (int a=1;a<=m;)
	{
		int b=a+1,s=p[a].d,x=p[a].x,y=p[a].y;
		while (b<=m && p[b].x==x && p[b].y==y)
		{
			if (s&p[b].d) return false;
			s|=p[b].d;
			b++;
		}

		int news=0;
		if (x==minx) news|=6;
		if (x==maxx) news|=9;
		if (y==miny) news|=12;
		if (y==maxy) news|=3;
		if (news&s) return false;
		s|=news;
		q[++k] = point(x,y,s);

		a=b;
	}
	sort(q+1,q+k+1);
	for (int a=1;a<=n2;a++)
	{
		int x=hori[a].x,y1=hori[a].l,y2=hori[a].r,s=hori[a].d;
		int l=0,r=k;
		while (l+1!=r)
		{
			int m=(l+r)>>1;
			if (q[m].x>x || (q[m].x==x && q[m].y>y1)) r=m;
			else l=m;
		}
		while (r<=k && q[r].x==x && q[r].y<y2)
		{
			if (q[r].d&s) return false;
			q[r].d|=s;
			r++;
		}
	}

	sort(q+1,q+k+1,cmp);
	for (int a=1;a<=n1;a++)
	{
		int y=vert[a].y,x1=vert[a].l,x2=vert[a].r,s=vert[a].d;
		int l=0,r=k;
		while (l+1!=r)
		{
			int m=(l+r)>>1;
			if (q[m].y>y || (q[m].y==y && q[m].x>x1)) r=m;
			else l=m;
		}
		while (r<=k && q[r].y==y && q[r].x<x2)
		{
			if (q[r].d&s) return false;
			q[r].d|=s;
			r++;
		}
	}
	return true;

	/*int l=0,r=n1;
	  while (l+1!=r)
	  {
	  int m=(l+r)>>1;
	  if (vert[m].y >= y) r=m;
	  else l=m;
	  }
	  while (r<=n1 && vert[r].y==y)
	  {
	  if (x>vert[r].l && x<vert[r].r)
	  {
	  if (s&vert[r].d) return false;
	  s|=vert[r].d;
	  }
	  r++;
	  }
	  l=0,r=n2;
	  while (l+1!=r)
	  {
	  int m=(l+r)>>1;
	  if (hori[m].x >= x) r=m;
	  else l=m;
	  }
	  while (r<=n1 && hori[r].x==x)
	  {
	  if (y>hori[r].l && y<hori[r].r)
	  {
	  if (s&hori[r].d) return false;
	  s|=hori[r].d;
	  }
	  r++;
	  }
	  if (s!=15) return false;*/
	return true;
}

int main()
{
	int t;
	scanf("%d",&t);
	for (;t--;)
	{
		scanf("%d",&n);
		for (int a=0;a<n;a++)
			for (int b=0;b<4;b++)
				scanf("%d",&rectangles[a][b]);
		if (isRectangleCover()) printf("Perfect
");
		else printf("Guguwansui
");
	}

	return 0;
}