折半(二分查找):
举例:
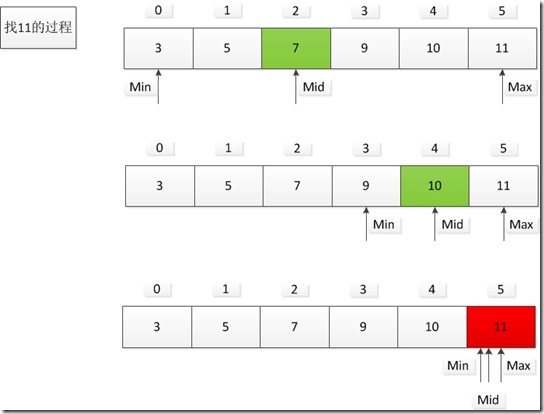
class BiSearch { /* 折半(二分)查找: 算法思想: 要求序列必须有序(升序/降序),因为只有这样才能确定 数据的范围,通过不断的折半来缩小查找数据的范围 设查找数据为key ①通过两个变量min和max来指定数据的范围,要求min<=max (min=max表示只有一个数据时) ②首先与mid=(min+max)/2比较,如果key=mid查找成功,直接返回 mid,如果key<mid,则min=mid-1,缩短查找范围,此时在让key与 mid=(max+min)/2比较,若key>mid,则max=mid+1,之后再与新的mid 比较,依次类推找到则返回,未找到则min>max. */ public static int biSearch(int[] arr,int key) { int max=arr.length-1,min=0,mid; while(max>=min) { mid=(max+min)/2; if(key==arr[mid]) return mid;//返回key在数组中的下标 else if(key<arr[mid]) max=mid-1; else min=mid+1; } return -1;//表示未找到 } public static void main(String[] args) { int[] arr={3,5,7,9,10,11}; System.out.println("keyIndex="+biSearch(arr,11)); } }折半查找过程(以上面为例)
查找成功:
示例2:
已知有序数组,要求在有序数组中插入一个元素,使之仍然有序.
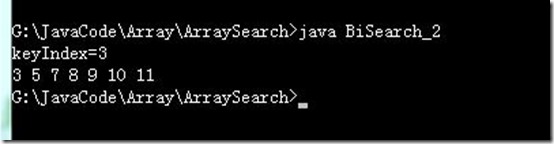
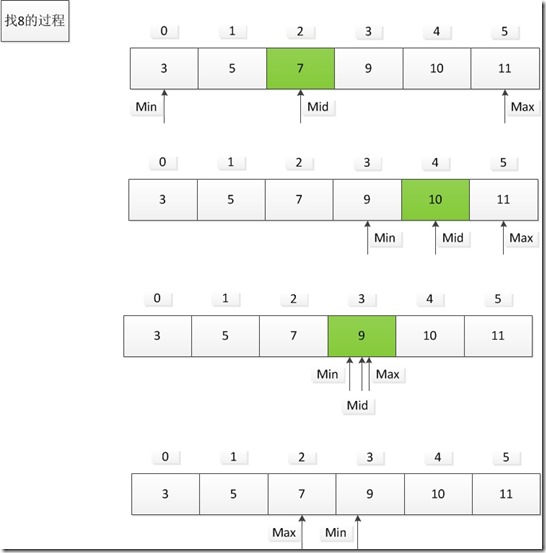
class BiSearch_2 { //已知有序数组,要求在有序数组中插入一个元素,使之仍然有序 /* 思想: ①首先我们要找到该元素插入的位置,才能进行操作 ②由于数组有序,通过折半查找来确定其位置 ③把该位置(包括这个位置)的元素(从后向前)逐个后移, 为新插入的元素 空出一个位置 */ public static int biSearch(int[] arr,int key) { int max=arr.length-2,min=0,mid; while(max>=min) { mid=(max+min)/2; if(key==arr[mid]) return mid;//返回key在数组中的下标 else if(key<arr[mid]) max=mid-1; else min=mid+1; } return min;//由图可知min就是该元素的插入位置 } //数组中的元素后移,即赋值过程 public static void backWard(int[] arr,int site,int key)//site为插入位置 { int i; for(i=arr.length-2;i>=site;--i)//例子:site=3,arr.length=7 arr[i+1]=arr[i]; arr[i+1]=key;//此时i=2,因此插入位置为i+1 } public static void main(String[] args) { int[] arr={3,5,7,9,10,11,0};//已知数组的元素为6个,最后一个0 //为了让数组多开辟一个空间,存放插入元素 int index; index=biSearch(arr,8); System.out.println("keyIndex="+index); backWard(arr,index,8); //打印 for(int i=0;i<arr.length;++i) System.out.print(arr[i]+""); } }运行结果:注意:折半查找优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。
进制转换:
①十进制转二进制(除二取余法,仅适用于正数)class ArrayTest_2 { //十进制转二进制 /* 算法思想: ①利用乘2取余的方法 ②考虑到是逆序输出可以用顺序栈(后进先出)方式输出 */ public static void toBi(int number) { int[] stack=new int[32]; int top=-1;//栈顶指针(类似指针功能) while(number!=0) { stack[++top]=number%2; number/=2; } while(top!=-1)//出栈 System.out.print(stack[top--]); } //法二,利用java中提供的方法 public static void toBi_2(int number) { StringBuffer sb=new StringBuffer();//定义了一个存数据的容器 while(number!=0) { sb.append(number%2);//向容器中添加 number/=2; } System.out.print(sb.reverse());//通过StringBuffer中的reverse功能 //逆序输出 } public static void main(String[] args) { toBi(20); System.out.println(); toBi_2(20); } /* 该方法只能计算正数 */ }
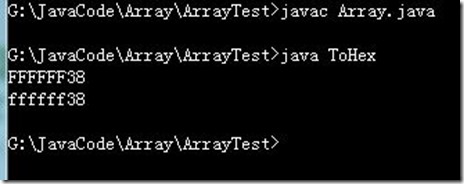
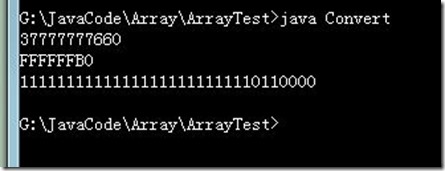
class ToHex { //十进制-->十六进制 /* 算法思想: ①首先该数与低四位为1,其余位为0(15)数相与(&)可得到该数低四位 ②使该数右移(>>>)四位,在与15相与又得到四位,依此类推 知道原数变为0停止 注意:这里用>>>而不用>>原因是考虑到负数会一直补1, 当然可以通过-1(补码全为1)来决定结束,但无法输出 符号位的十六进制,而>>>可以把负数的符号位也转成 十六进制 */ public static void toHex(int number) { StringBuffer sb=new StringBuffer();//定义了一个存数据的容器 int Hex; while(number!=0) //for(int i=0;i<8;++i)//强制把32位都转换:200->0000C8 { //而while则为:C8 Hex=number&15; if(Hex>=10) sb.append((char)(Hex-10+'A')); else sb.append(Hex); number >>>= 4; } System.out.print(sb.reverse()); } public static void main(String[] args) { toHex(-200); System.out.println("\n"+Integer.toHexString(-200)); } }
二维数组:
在Java中并没有真正的多维数组,只有数组的数组,虽然在应用上很像C语言中的多维数组,但还是有区别的.在C语言中定义一个二维数组,必须是一个x*y的二维矩阵块.而Java中的多维数组并不一定是规则的矩阵形式定义一个多维数组:int[][] xx;//int xx[][],int[] xx[];它表示一个数组引用变量xx,第一个元素变量为xx[0],第n个元素变量为xx[n-1]. xx中的每个元素变量(xx[0]~xx[n-1])正好又是一个整数类型的数组引用变量.
int[ ][ ] xx;
xx=new int[3][ ];
解析:这两句代码表示数组xx有三个元素,每个元素都是int[ ]类型的一维数组.相当于定义了三个数组引用变量,分别为:int[ ] xx[0],int[ ] xx[1],int[ ] xx[2].
由于xx[0],xx[1],xx[2]都是数组引用变量,必须对它们赋值,指向真正的数组对象.才可以引用这些数组中的
元素.
xx[0]=new int[3];
xx[1]=new int[2];
另:
二维数组的静态初始化:
int[ ][ ] xx={{3,2,7},{1,5},{6}};
另附上 陈吉斯汗同学的关于java数组的总结,个人认为很不错:http://bdcwl.blog.163.com/blog/static/7652226520091024067604/
示例1:
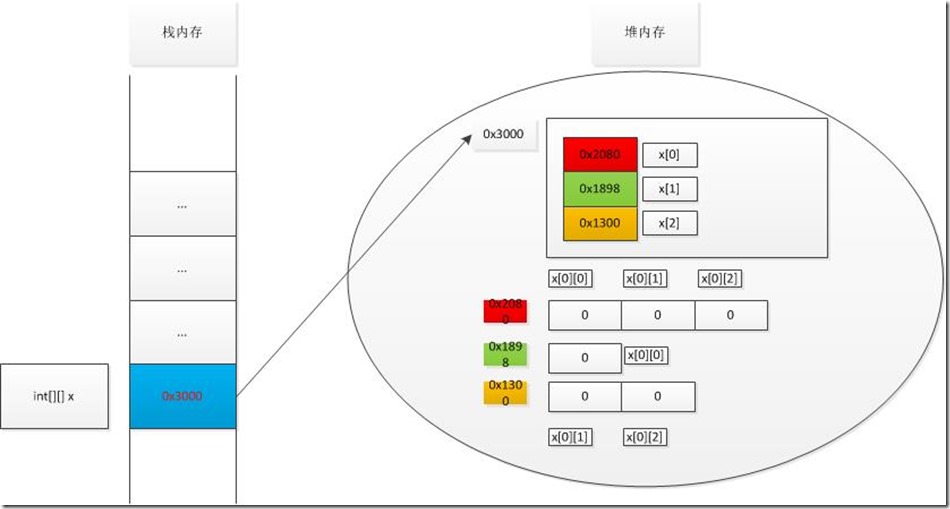
class ArrayDemo1 { public static void main(String[] args) { int[] arr = new int[2];//建议这种方式,定义一个int型数组的引用变量 arr int arr[] = new int[2]; //静态初始化 int[] arr = new int[]{3,1};//new int[]中不能指定长度,编译不能通过 //可能出现元素个数和指定长度不同 int[] arr = {3,1};//静态初始化简化形式 System.out.println(arr[3]);//编译可以通过,编译时期没有创建数组也就是说在运行时期才在堆内存中为数组开辟空间. //在运行时期发生数组角标越界异常 arr=null; System.out.println(arr.length);//编译依然可以通过,原因同上. //运行时期发生错误,arr不再引用数组,无法操作数组中的元素 //发出空指针异常 //二维数组静态初始化 int[][]a=new int[][]{{4,2},{5,6,7}};//① //int[][]a={{4,2},{5,6,7}};//等价于① } }示例2:class DoubleArray { public static void main(String[] args) { int[][] xx=new int[3][2];//二维数组中的三个元素,每个元素指向一个长度为2的一维数组System.out.println("x\t"+xx);//[[代表二维数组,I->Integer(整形),数组中的元素类型 //@后面由哈希函数算出哈希址 System.out.println("x[0]\t"+xx[0]); int[][] y=new int[4][]; System.out.println("y\t"+y); System.out.println("y[0]\t"+y[0]); int[][] x=new int[3][];//每个引用数组的长度可以不一样 x[0]=new int[3]; //在内存中的情况如下图: x[1]=new int[1]; x[2]=new int[2]; } }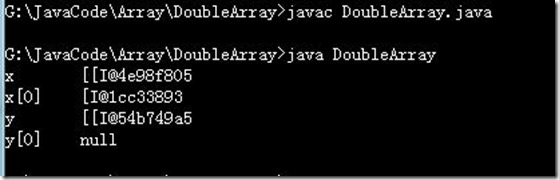
二维数组在内存中:
