一、什么是逻辑代数
又叫布尔代数、开关代数。它是反映事物之间的因果关系,反映和处理逻辑关系的数学工具。它的变量值只有真或假(即1、0),分别代表两种状态。正是这一点,它可以很好的和二进制以及现代的数字电路结合在一起,实现现代计算机的复杂计算功能。布尔用数学方法研究逻辑问题,成功地建立了逻辑演算。他用等式表示判断,把推理看作等式的变换。这种变换的有效性不依赖人们对符号的解释,只依赖于符号的组合规律 。这一逻辑理论人们常称它为布尔代数。20世纪30年代,逻辑代数在电路系统上获得应用,随后,由于电子技术与计算机的发展,出现各种复杂的大系统,它们的变换规律也遵守布尔所揭示的规律。

二、基本概念、公式、定理
2.1、逻辑常量与变量
逻辑常量只有两个,即0和1,用来表示两个对立的逻辑状态。逻辑变量与普通代数一样,也可以用字母、符号、数字及其组合来表示,但它们之间有着本质区别,因为逻辑常量的取值只有两个,即0和1,而没有中间值。
2.2、基本逻辑关系
- 与:当决定一事件的所有条件都具备时,事件才发生
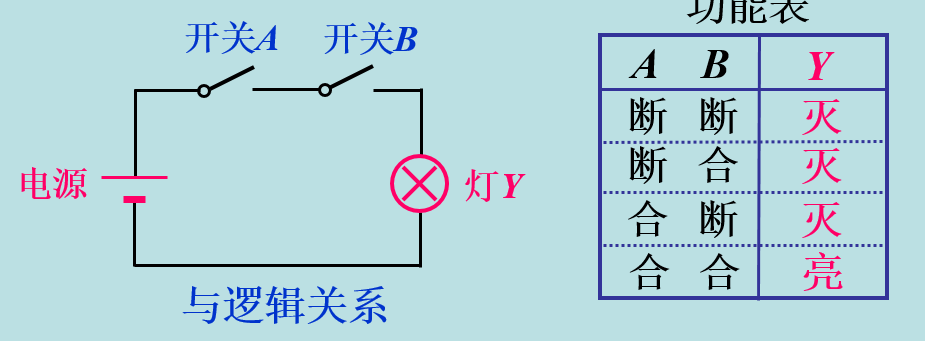
- 或:决定一事件是否发生的诸多条件中,只要有一个或多个具备时就发生

- 非:只要条件具备,事件就不会发生,条件不具备,事件就一定会发生

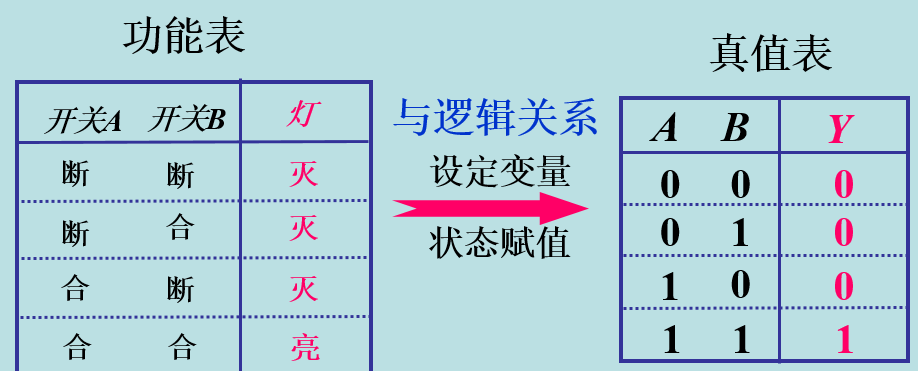
2.3、真值表
表征逻辑事件输入和输出之间全部可能状态的表格。列出命题公式真假值的表。通常以1表示真,0 表示假。命题公式的取值由组成命题公式的命题变元的取值和命题联结词决定,命题联结词的真值表给出了真假值的算法。真值表是在逻辑中使用的一类数学表,用来确定一个表达式是否为真或有效。 (表达式可以是论证;就是说,表达式的合取,它的每个结合项(conjunct)都是最后要做的结论的一个前提。)
构造真值表步骤:
- 找出命题公式中所含的所有命题变项(若无下角标就按字典顺序给出),列出所有的可能的赋值
- 按从低到高的顺序写出各层次
- 对应每个赋值,计算命题公式各层次的值,直到最后计算出命题公式的值
上面三种基本逻辑关系的真值表如下:


2.4、逻辑函数
逻辑函数是由逻辑变量、常量通过运算符连接起来的代数式。同样,逻辑函数也可以用表格和图形的形式表示。
2.5、逻辑运算
在逻辑代数中,有与、或、非三种基本逻辑运算。表示逻辑运算的方法有多种,如语句描述、逻辑代数式、真值表、卡诺图等。
- 与运算
Y=A.B=AB - 或运算
Y=A+B - 非运算
Y=Ã
2.6、定理
- 交换律
A.B=B.A
A+B=B+A - 结合律
(A.B).C=A.(B.C)
(A+B)+C=A+(B+C) - 分配律
A(B+C)=AB+AC
A+BC=(A+B)(A+C)
三、逻辑运算与门电路
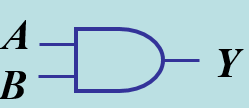
电子工程师设计了门电路来进行逻辑运算,基本门电路如下:
- 与门:Y=A.B
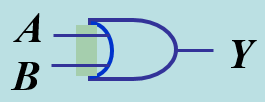
- 或门:Y=A+B
- 非门:Y=Ã
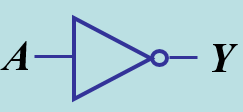
然后通过这些基础的门电路组合设计出更复杂的数字电路,最终构成了我们使用的现代计算机。