在马尔科夫模型(MDP)完全已知的情况下,我们可以用动态规划来求解最优策略,求出在给定状态$s$下,应该选择哪一个 下个状态$s'$,这样使得累积奖励最大。
因为需要求解的是累积奖励,所以单纯的贪婪即时奖励最大的策略是不可行的。
所以我们引入了能够包含未来奖励的v值(和q值),在与环境的交互过程中,更新v值从而得到更好的策略,得到更大的累积奖励。
在前几篇中,为了便于理解,我们的v值(和q值)是离散的,是一张表。比如q表,就是一个状态数*动作数的大表,每一行是对应状态$s$可选的动作$a$的q值。这样一来,到达某一状态时,我们只需要查询q表,找到给定状态$s$对应的行,对比哪个动作$a$的q值高,就选择哪个动作$a$就好。
策略评估
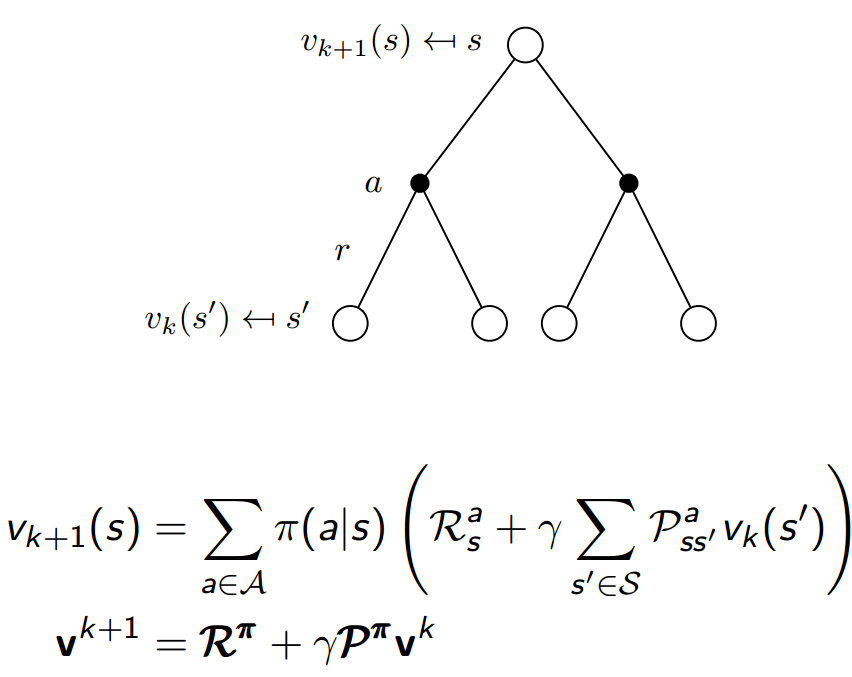
给定策略$pi$,在每一步的迭代$k$中,对所有的状态$s in S$,利用贝尔曼公式根据$v_{k-1}(s')$求$v_k(s)$,多次迭代至$v_pi$会收敛。
$s'$是$s$的下一个状态,$v(s)$更新的时候需要用到$v(s')$,$v(s)=R+gamma v(s')$。
在第$k+1$次迭代,更新状态$s$的$v_{k+1}(s)$时,状态$s'$的$v_{k+1}(s')$还未更新,
我们就用上一次迭代$k$的结果$v_{k}(s'),来更新$v_{k+1}(s)$,公式如下:
策略迭代
由于值函数$v(s)$中包含了未来状态的奖励,所以整个动态规划问题可以拆成一个个子问题,子问题最优即是全局最优。
所以我们的策略其实就是对待每一个子问题给定状态$s$下,在下一步可到达的状态$s'$里,选择$v(s')$值最大的状态$s'$,即贪心策略。不同的v值就对应了贪心的选择不同,即不同的策略$pi$。
$pi' = greedy(v_pi)$
在上个小节我们迭代收敛得到了新的$v_pi$后,就可以依据新的$v_pi$改进我们的策略$pi$。改进的策略$pi$又可以继续迭代收敛到新的$v_pi$,如此循环,最终收敛至$pi^*$。
在这样的更新方式中,我们评估了这个策略得到稳定值后,再改进这个策略,称之为同策略学习(On-Policy learning)。

值迭代
在策略迭代中,我们针对每次的策略$pi$都先不断迭代至收敛的$v_pi$之后,再来改进这个策略$pi$。
为了加快收敛速度,我们可以在$v_pi$还没有收敛的迭代过程中,就立马改进策略$pi$,再循环这个过程。
$s'$是$s$的下一个状态,$v(s)$更新的时候需要用到$v(s')$,$v(s)=R+gamma v(s')$。
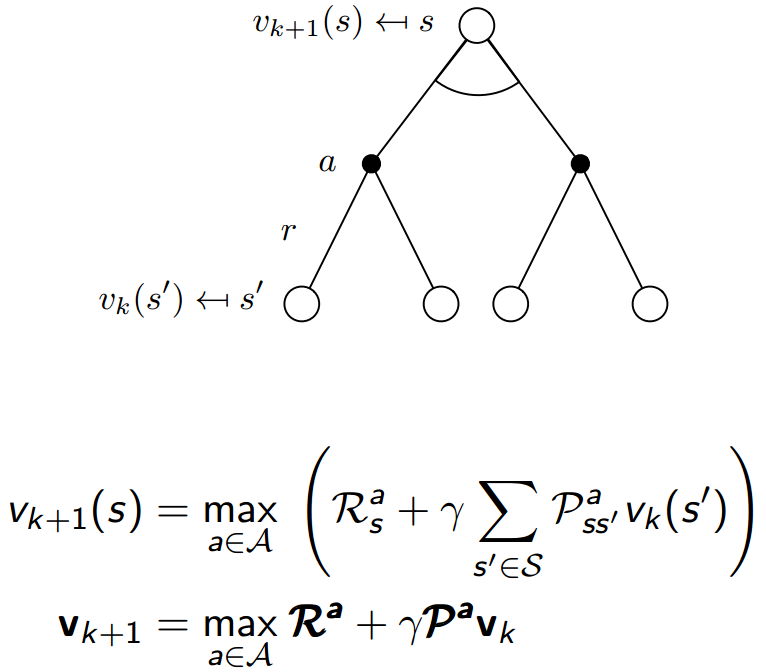
在第$k+1$次迭代,更新状态$s$的$v_{k+1}(s)$时,$v_pi$还没有收敛,就立马利用第$k$次迭代更新结果,改进策略$pi$。
在这样的更新方式中,我们边评估策略,边改进策略,称之为异策略学习(Off-Policy learning)。
我们的策略是根据v值的贪婪策略,$pi' = greedy(v_pi)$,所以贪心max的更新公式如下:
参考:
1. David Silver 课程
2. Reinforcement learning: An Introduction. Richard S. Sutton