11.7 模拟赛
模拟赛鸽了几天没写题解了。。
T1 煎蛋的疑惑
考虑每一个左括号表示+1,一个右括号-1,那么画出来的图是这样的
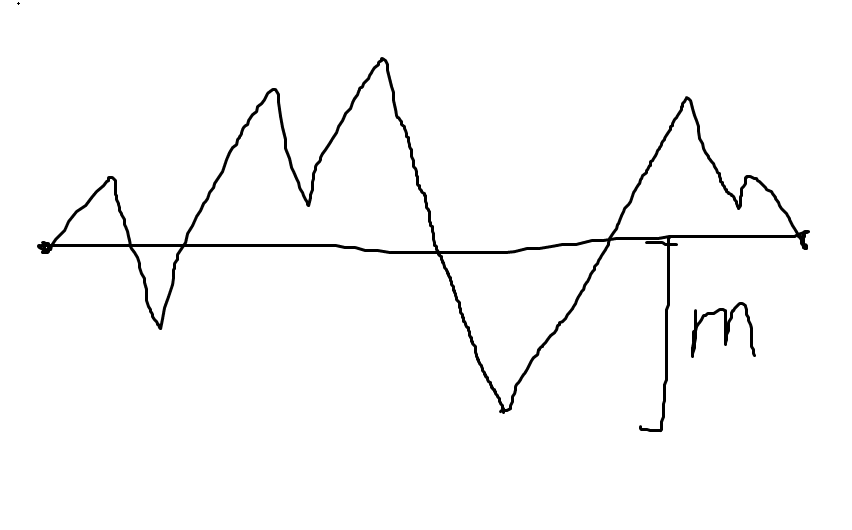
考虑把沿着 $ x = -m $ 翻折一下,也就是终点变成了 $ (2n , -2m) $
然后假设一次上升为 +1 一次下降为 -1 那么我们相当于是要钦定 $ n - m $ 个位置上升, $ n + m $ 个位置下降。那么如果我们钦定 $ n + m $ 个位置下降是不是就做完了呢?并不是,然而 $ n + m $ 个位置下降仍然会导致一种非法情况
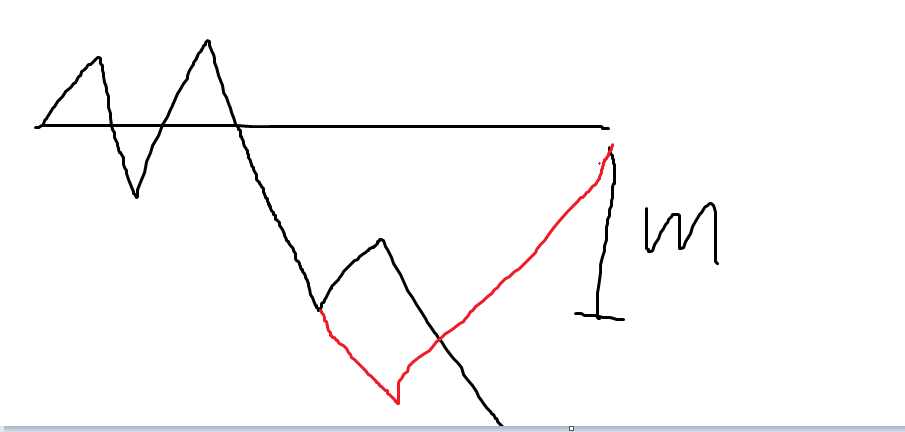
当然这种情况告诉我们,最低点其实是 小于 $ m $ 而不是等于 $ m $ ,当前缀和减一下就好了。
答案 $ C_{2n}^{n+m} - C_{2n}^{n+m+1} $
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
#define MAXN 1000006
#define int long long
#define P 998244353
int n , m;
int J[MAXN << 1];
int power( int a , int x ) {
int ans = 1 , cur = a % P;
while( x ) {
if( x & 1 ) ans *= cur , ans %= P;
cur *= cur , cur %= P , x >>= 1;
}
return ans;
}
int C( int a , int b ) {
return J[a] * power( J[b] * J[a - b] % P , P - 2 ) % P;
}
signed main() {
cin >> n >> m;
J[0] = 1; for( int i = 1 ; i < MAXN * 2 ; ++ i ) J[i] = J[i - 1] * i % P;
cout << ( C( 2 * n , n + m ) - C( 2 * n , n + m + 1 ) + P ) % P << endl;
}
T2 蘑菇
考虑“每个联通块大小积”的组合意义,就是把再每个连通块中选一个点方案数之和。于是我们可以当作 这个题 的弱化版了。
就是设 $ f(x,0) $ 表示以 $ x $ 为根的子树中 $ x $ 所在的连通块中没有选择点的方案数, $ f(x , 1) $ 表示 $ x $ 为根的子树中 $ x $ 所在的连通块中有选择点的方案数。
考虑转移, $ f( u , 0 ) = prod ( f(v , 1) + f(v , 0) ) $ 因为如果子树中已有 1 我们可以选择断开这条边,如果子树中没有 1 我们必须选择连上这条边这个点的选择方法有这些,可以加法原理加起来,再根据乘法原理相乘。
$ f(u,1) = f(u,1) imes (f(v,0) + f(v,1)) + f(u,0) imes f(v,1) $
考虑这个点之前没有被选过,那么必须儿子是被选择过且连接这条边。 如果这个点之前被选择过了,儿子可以选择可以不选择,选择过断开这个边就行了。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
#define MAXN 1000006
#define P 998244353
#define pb push_back
typedef long long ll;
int n;
ll w = ( P + 1 ) / 2 , W = 1;
ll dp[MAXN][2];
int read( ) {
char ch = ' '; int ret = 0;
while( ch > '9' || ch < '0' ) ch = getchar();
while( ch <= '9' && ch >= '0' ) ret *= 10 , ret += ch - '0' , ch = getchar();
return ret;
}
int head[MAXN] , to[MAXN << 1] , nex[MAXN << 1] , ecn;
void ade( int u , int v ) {
to[++ ecn] = v , nex[ecn] = head[u] , head[u] = ecn;
to[++ ecn] = u , nex[ecn] = head[v] , head[v] = ecn;
}
void dfs( int u , int fa ) {
dp[u][1] = dp[u][0] = 1;
for( int i = head[u] ; i ; i = nex[i] ) {
int v = to[i];
if( v == fa ) continue;
dfs( v , u );
dp[u][1] = 1LL * ( 1LL * dp[u][0] * dp[v][1] % P + 1LL * dp[u][1] * ( dp[v][0] + dp[v][1] ) % P ) % P;
dp[u][0] *= 1LL * dp[v][0] + dp[v][1] , dp[u][0] %= P;
}
}
signed main() {
cin >> n;
for( int i = 1 , u , v ; i < n ; ++ i ) u = read() , v = read( ) , ade( u , v ) , W *= w , W %= P;
dfs( 1 , 1 );
cout << 1LL * dp[1][1] * W % P << endl;
}
T3 墙
考虑 $ O(n^2) $ 空间就比较简单,用 $ dp[i][j] $ 表示当前在 $ i $ 上一个位置在 $ j $ 的方案数,其中 $ a_i < a_j $ 则表示当前在下降,否则表示上前在上升。
但是这题 卡 空 间 ....
考虑 $ up(i) $ 表示当前的值为 $ i $,从这里开始先向下按照一下一上移动,最后在上升的方案数,设 $ dw(i) $ 表示当前值为 $ i $ 从这里开始向上一下一上移动,最后在上升的方案数。最后我们把所有 $ up(i) $ 加起来,但是这样只算完了一半,剩下一半可以一样地计算了。
考虑怎么转移 $ up( i ) $ ,首先从大到小枚举 $ i $ ,然后从小到大枚举 $ j $ 然后分类
- 如果 $ j $ 的位置在 $ i $ 的后面,可以直接用 $ j $ 来更新 $ i $
- 否则,可以直接用 $ i $ 转移到 $ j $
为什么这样计算是正确的呢?考虑什么时候 $ i $ 会更新之前的 $ j $ ,如果 $ i $ 会更新之前的 $ j $ ,说明所有更新 $ i $ 的点都比 $ j $ 小,因为只有比 $ j $ 小的点此时更新了 $ j $ 。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define MAXN 6006
int n , P , res = 0;
int A[MAXN] , pos[MAXN];
int up[MAXN] , dw[MAXN];
int main() {
cin >> n >> P;
for( int i = 1 ; i <= n ; ++ i ) scanf("%d",&A[i]) , pos[A[i]] = i , up[i] = 1 , dw[i] = 0;
for( int i = n ; i >= 1 ; -- i )
for( int j = 1 ; j < i ; ++ j )
if( pos[j] > pos[i] ) up[i] += dw[j] , up[i] %= P;
else dw[j] += up[i] , dw[j] %= P;
for( int i = 1 ; i <= n ; ++ i ) res += up[i] , res %= P , up[i] = 1 , dw[i] = 0;
for( int i = 1 ; i <= n ; ++ i )
for( int j = n ; j > i ; -- j )
if( pos[j] > pos[i] ) up[i] += dw[j] , up[i] %= P;
else dw[j] += up[i] , dw[j] %= P;
for( int i = 1 ; i <= n ; ++ i ) res += up[i] , res %= P;
cout << ( ( res - n ) % P + P ) % P << endl;
}