【计算导论与程序设计】PPT整理 2021.11

程序语言设计概述（略）

单元一：程序设计语言（挖坑）

程序设计语言初步（一）

程序设计语言初步（二）

单元二：计算与算法（挖坑）

计算过程与算法（一）

计算过程与算法（二）

单元三：问题求解方法

程序设计方法（挖坑）

算法设计方法（子程序）

1.子程序概念及设计

• 子程序的定义：子程序是封装并给以命名的一段程序代码，这段程序代码完成子程序所定义的功能，可供调用。
• 封装：调用者只需要关心代码能完成什么功能，如何调用代码（即子程序接口），而不需要关心代码的内部实现。
• 子程序很重要的特点：调用者只需要关心子程序接口，不必了解子程序内部实现细节。
• 子程序的控制和调用机制：通过子程序名进行调用；调用时需要传递一些供子程序计算和处理的数据（参数）；子程序执行完成后需要返回处理结果；子程序可以调用其他的子程序；
• 引入子程序的目的：
  1.程序“复用”，避免在程序中使用重复代码
  2.结构化程序设计的需要
  3.使程序的调试和维护变得更加容易
• 子程序设计原则
  1.高内聚：功能相对独立和完整；
  2.低耦合：与外界（调用者）的关系尽量松散，不要太紧密，使其能方便地被重用；

2.C语言的函数

• 函数设计的要求：明确该函数的功能（函数应该只完成单一的任务）；定义该函数的接口（即函数头，包括函数名、参数表和返回值类型）定义该函数的功能实现部分
• 如果不列出参数的类型，编译器就假定其为int类型
• 如果函数不接收任何参数，则参数列表定义为void ；如 int print(void)
• 函数中的语句可以访问本函数中定义的参数、变量，但是不能访问其他函数中定义的参数和变量
• 不允许在一个C函数的内部定义另一个函数
• 调用时，会为形参分配内存，然后将实参的值复制一份到形参中。实参的个数、类型和顺序，应该与形参个数、类型和顺序一致，才能正确地进行数据传递。

函数调用过程：

1. 给被调用函数分配存储空间；
2. 计算实际参数表达式的值；
3. 把实际参数的值按赋值转换规则转换成形式参数的类型。
4. 把转换后的实际参数（实参）的值送入形式参数（形参）中。
5. 运行调用函数中的语句；
6. 计算返回值表达式的值，并转换成函数的结果类型；
7. 释放被调用函数占用的存储空间；
8. 带着转换后的值返回调用函数。

• 形参变量只有在被调用时，才分配内存单元；调用结束时，即刻释放所分配的内存单元。

• 实参和形参占用不同的内存单元，即使同名也互不影响。（此处实参是变量的情况）

• 实参对形参的数据传送是单向的，即只能把实参的值传送给形参，而不能把形参的值反向传送给实参。

• 不同函数中可以使用相同名称和类型的变量，它们占用不同的内存单元，互不影响。

• 函数原型的作用：函数原型是对被调用函数的接口声明，它告诉编译器函数返回的数据类型、函数所要接收的参数个数、参数类型和参数顺序，编译器用函数原型校验函数调用是否正确。

• 函数原型的位置：

1. 可以放置在任何函数之外，出现在该函数原型之后的所有函数都可以调用对应的函数；
2. 也可以放在某个函数中，此时只有该函数能够调用它；
3. 从程序设计风格考虑，最好是将函数原型集中在一起，放在主函数之前。
4. 当被调用函数的函数定义出现在该函数调用之前时，可以省略函数原型。因为在调用之前，编译系统已经知道了被调用函数的函数类型、参数个数、类型和顺序。
5. 如果程序中没有包含函数原型，则编译器就会用第一次出现的该函数（函数定义或函数调用）来构造函数原型。默认情况下，编译器假定函数的返回类型为int类型，而对参数不作任何假定。

强烈建议使用函数原型并写在main函数之前。如果不使用函数原型,那么就要保证所有函数被调用前,都必须要保证该函数被定义,即要考虑函数定义的位置,假设函数A调用了B,B中又调用了C,C中又调用了D,那么就要保证函数D定义在C前,C定义在B前,B定义在A前,那是给自己找麻烦,还不如在一开始使用函数原型,就不需要考虑定义位置

• 函数原型可以用来强制转换参数类型。

3.子程序（函数）调用过程及原理

• 函数的调用和执行的实质是控制转移，调用函数时，将控制转到被调用的函数，被调函数执行结束时，则将控制转回主调函数，继续执行后续的操作
  （有关下图的详细情况请点我）
  

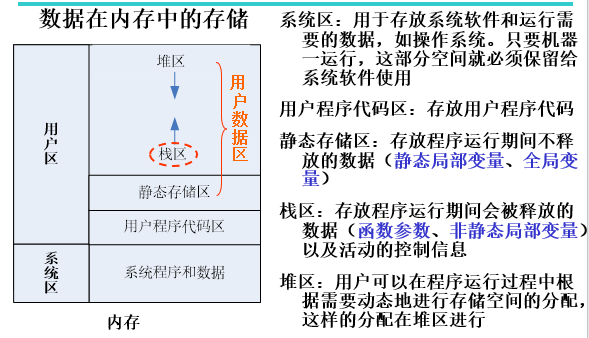
栈区：一片存放用户数据的内存空间；一端“封”了口（栈底），一端“开”着口(栈顶)；保存数据：数据只能从顶部（栈顶）进入；取数据：栈顶的数据先被取出，栈底的数据最后被取出。即数据是“先进后出”。数据的进入和退出均在栈顶进行。读数据：只能读取栈顶的数据

开辟新的运行环境：

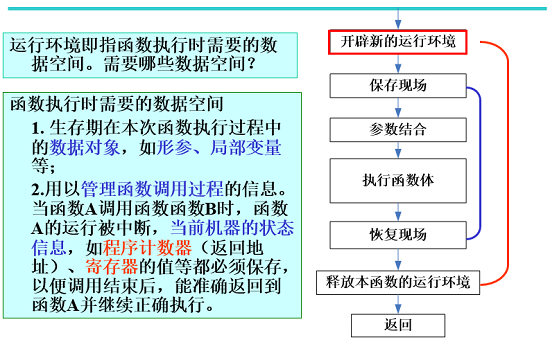
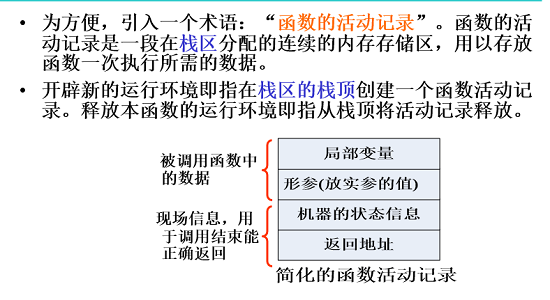
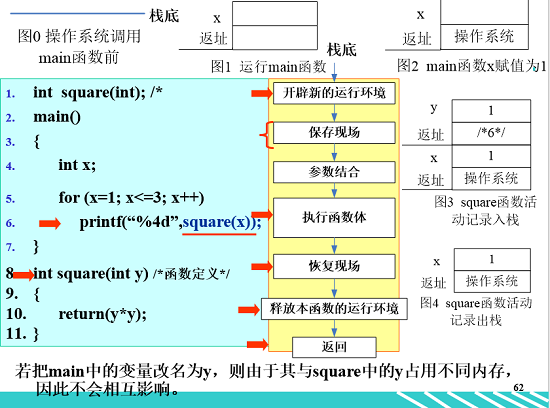
如何确保能够逐层返回到上一级调用？
函数A调用函数B，则在函数B的活动记录中记录了A的返回地址。返回前取出该地址，即能正确返回。
为何不同的函数可以使用同名的参数和变量？
因为不同函数的活动记录占用不同的内存单元，程序运行时始终是从位于栈顶的活动记录中取形参和变量的值。


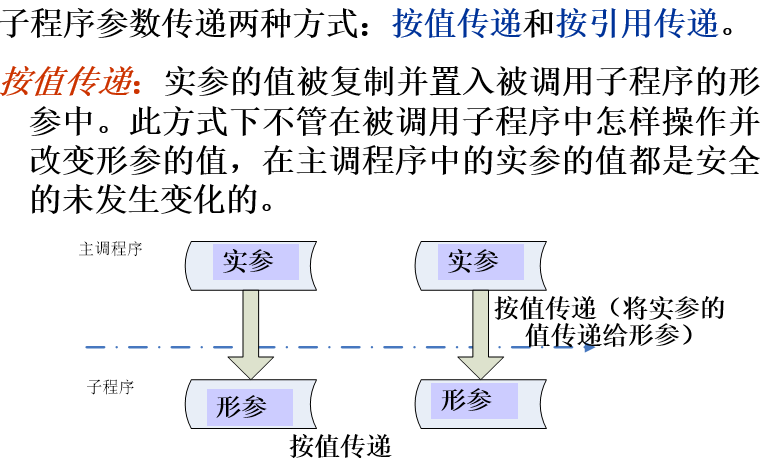
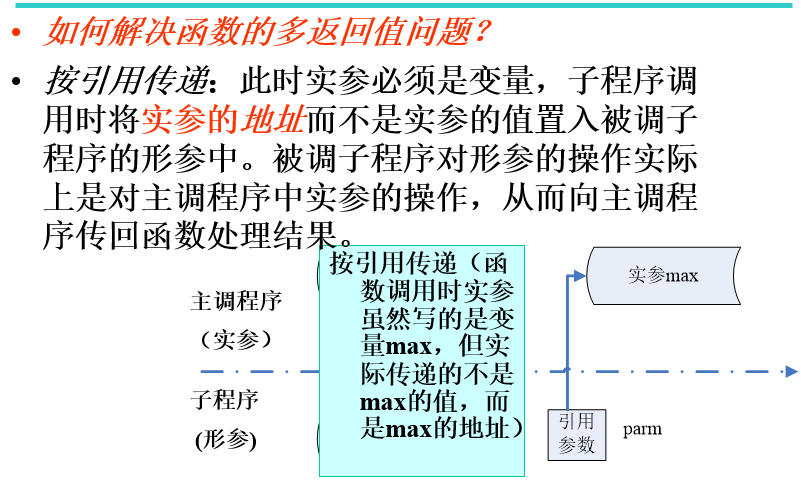
注意：C语言中所有的调用都是传值调用，但是可以通过其他方式来实现函数的多返回值(即实参本身存放的就是某个变量的内存地址，将该地址传递给被调用函数后，被调用函数通过该地址来访问变量，将函数处理结果写入变量)。

单元三：问题求解方法

递归算法设计

• 原始递归函数在可计算性理论中占有重要地位，是一种算法思想和计算模型。
• 递归（英语：Recursion），又译为递回，在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。递归表达了两个意思：“递推＋回归”。 这正是递归思想的精华所在。

表达式的定义是一个递归的形式，由下面四条规则构成:

1. 常量、变量、函数调用是表达式。
2. 如果Ω是表达式，则(Ω)是表达式；如果θ是单目运算符，θ允许前缀形式，则θΩ是表达式；如果θ允许后缀形式，Ωθ是表达式。
3. 如果Ωl、Ω2、Ω3是表达式，θ是双目运算符，则ΩlθΩ2是表达式；θ1和θ2构成三目运算符，则Ωlθ1Ω2θ2Ω3是表达式。
4. 只有有限次的使用上述规则得到的有限长度的字符串式子，才是表达式。