Definition&Solution
对于一个给定的链表,如何判定它是否存在环以及环的长度问题,可以使用Floyd消圈算法求出。
从某种意义上来讲,带环的链表在本质上是一个有向图
考虑下面的事实:假定小Y和小Z在圆形操场上跑步,小Z的速度是小Y的两倍,那么总存在一个时刻,使得小Z和小Y在同一个位置但是小Z比小Y多跑了若干圈。
该算法的复杂度为O(n)。
代码如下:
void floyd_c() { int c1=list_begin,c2=list_begin;//c=child do { c1=nxt[c1]; c2=nxt[c2]; dosth(); c2=nxt[c2]; dosth(); } while(c1!=c2); return; }
其中dosth应具体情况具体分析。
考虑如何求出该环的起点。
如果你不理解环为什么有起点,不妨观察下面的链表:
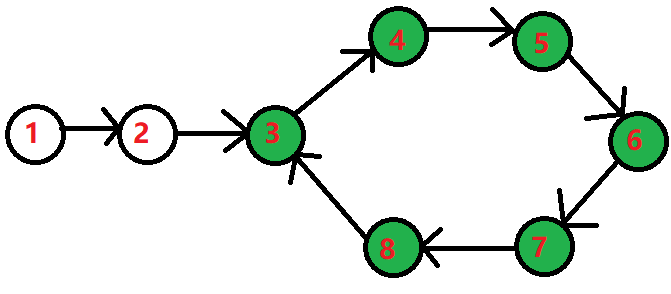
由于1是链表的起点,以1号点为起点遍历整张链表,是从3号点进入原谅环的,我们认为3号点是原谅环的起点。
如何求出起点。
将小Z和小Y都放到链表的起点上,当两者相遇时,将其中一个指针再次放到起点上,二者再次相遇的位置就是环的起点。
证明如下:
由于含有多个环的链表可以通过数学归纳由含有一个环的链表证明,故不妨设所研究的链表只有一个环,同时还有一条长度至少为1(一个点)的链。
设环的长度为n,链的长度为m。快慢指针第一次相遇在环上的第k个点,那么有:
快指针的路程Sa=m+A*n+k,其中A∈Z,代表走了几圈①
慢指针的路程Sb=m+B*n+k。其中B∈Z,代表走了几圈②
由于快指针的速度是慢指针的两倍,即:
Va=2Vb③
在运动时间一定的情况下有:
Sa=2Sb④
①-②得:
Sa-Sb=(A-B)*n⑤
联立④⑤解得Sb=(A-B)*n⑥
由于A,B∈Z,且显然A>B,所以Sa,Sb都是圈长度的倍数。
不妨设Sb=T*n。显然从起点出发,走过T*n+m时,到达环的起点。
那么在两个指针相遇时,我们让两个指针的速度都为1,走m个单位就可以到达环的起点,这时快指针的路程为2Sb+m。慢指针的路程为Sb+m。
由于Sb=T*n,这时的路程可以理解为快指针走到m处然后绕了几圈,绕圈路程为2Sb,慢指针从路程为Sb的位置走了m,那么二者的相遇的地方显然是环的起点。
特别的,因为vb=1。所以Sb即为循环的次数。通过⑥式已经证明,该算法的复杂度为O(n)。其中常数随环的形态而改变。
Sample
UVA11549 Calculator Conundrum
Description
有一个非常无聊的傻逼,有一天他闲的没事干玩一个老式计算器,这个计算器只能显示答案最高的n位。比如n=2,计算99+1的答案为100时,显示为10。
现在他一开始输入了一个数字k,保证在能显示的范围内,然后将k平方,然后将答案平方,再平方……
这个无聊的人想知道屏幕上显示的最大数时多少。
Input
第一行是数据组数,对于每组数据,包含:
- 一个整数n,一个整数k
Output
对于每组数据,输出:
- 对应答案
Sample Input
2 1 6 2 99
Sample Output
9 99
Hint
n≤9
Solution
简单的数学归纳可以证明计算器上的数字是会出现循环的,可以使用Floyd消圈算法解决此题。
Code
#include<cstdio> #define rg register #define ci const int #define ll long long int inline void qr(int &x) { char ch=getchar(),lst=NULL; while(ch>'9'||ch<'0') lst=ch,ch=getchar(); while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); if (lst=='-') x=-x; } char buf[20]; inline void write(int x,const char aft,const bool pt) { if(x<0) {putchar('-');x=-x;} int top=0; do { buf[++top]=x%10+'0'; x/=10; } while(x); while(top) putchar(buf[top--]); if(pt) putchar(aft); } template <typename T> inline T mmax(const T &a,const T &b) {if(a>b) return a;return b;} template <typename T> inline T mmin(const T &a,const T &b) {if(a<b) return a;return b;} template <typename T> inline T mabs(const T &a) {if(a<0) return -a;return a;} template <typename T> inline void mswap(T &a,T &b) {T temp=a;a=b;b=temp;} int t,n,k,ans; int nxt(ci); int main() { qr(t); while(t--) { n=k=0;qr(n);qr(k); int c1=k,c2=k;ans=k; do { c1=nxt(c1); c2=nxt(c2);ans=mmax(ans,c2);c2=nxt(c2);ans=mmax(ans,c2); } while(c1!=c2); write(ans,' ',true); } return 0; } short bufff[100]; int nxt(int x) { if(!x)return 0; long long kf=(long long)x*x; int L=0; while(kf>0) bufff[L++]=kf%10,kf/=10; int temp=n; if(temp>L) temp=L; int sum=0; for(int i=0;i<temp;++i) sum=(sum<<1)+(sum<<3)+bufff[--L]; return sum; }
Summary
1、Floyd消圈算法是达到理论下限的判断有向图上环的算法。尽管它的常数难以控制,但是十分的实用并且好写。
2、在证明的最后使用了等效替代法,在其他的OI毒瘤题中,也应注意该方法的应用。