C [yLOI2019] 棠梨煎雪
Background
岁岁花藻檐下共将棠梨煎雪
自总角至你我某日辗转天边
天淡天青 宿雨沾襟
一年一会信笺却只见寥寥数言
——银临《棠梨煎雪》
Description
给定 (m) 个长度为 (n) 的可能含有 ? 的 01 串,其中 ? 既能代表 0 也能代表 1, (q) 次操作,每次给定一个区间,求有多少 01 串满足区间内的所有字符串都可以解释成该 01 串,或者单点修改某个字符串。
Limitations
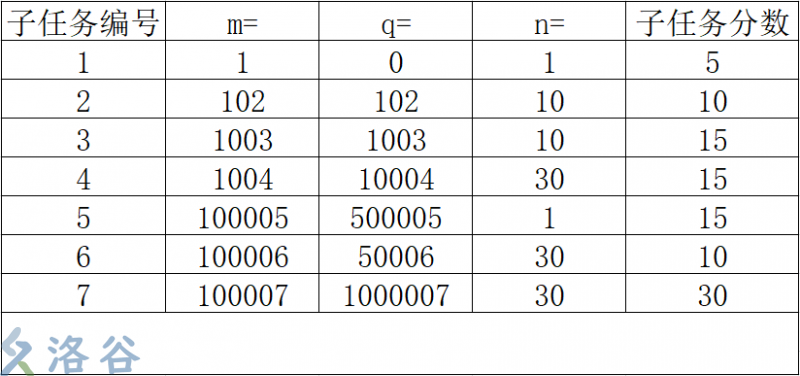
Solution
子任务 (1):
输出 (0) 即可得分,期望得分 (5~pts)。
子任务 (2):
考虑 (n) 只有 (10),因此可以 (O(2^n)) 去枚举所有可能的串,然后对于每个询问 (O(m)) 的逐个判定是否合法。时间复杂度 (O(qm2^n)),期望得分 (10~pts)。
子任务 (3):
考虑对于一段所有字符串的第 (x) 个字符,一共有四种可能:确定为 (0);确定为 (1);都可以;都不可以。如果 (0/1) 都不可以,则答案为 (0),因为不会有任何一个字符串匹配该区间。如果确定为某个数,则这一位只有一种可能;否则这一位有两种可能。根据乘法原理,如果有 (a) 个位置有两种可能,则本次询问的答案为 (2^a)。
因此对于每个询问,(O(nm)) 地去遍历区间内所有字符即可。时间复杂度 (O(nmq)),期望得分 (15~pts)。
子任务 (4):
考虑 (n) 只有 (30),可以状压到 int 中。具体的,维护两个 int,第一个 int 维护对应位是否确定是 (0) 或 (1),第二个 int 维护如果确定是 0 或 1 了那么具体是 0 还是 1。
例如,对于单个字符串,它所有的为 ? 的位置,在第一个 int 中对应位置是 0,所有为 0 或 1 的位置,在第在个 int 中对应的位置是 1,在第二个 int 中对应的位置是自身的值。
考虑 (a_1,~a_2) 是询问的左端点到某个字符串之前所维护的两个 int,(b_1,~b_2) 是该字符串的两个 int,现在合并这两个信息。
如果某一位置即不可以是 (1),也不可以是 (0),那么该字符串不为 ? 的位置在 (b_2) 中对应的值应该至少有一个和 (a_2) 中对应位置的值且 (a_1) 的该位置为 (1),位运算可以表现为 ((a1~&~b_1)~&~(a_2~oplus~b_2) ~
eq 0),则该询问的答案为 (0)。
否则这两段信息可以合并:将他们已经确定字符的位置合并起来,然后将确定位置对应的值合并起来即可。于是 (a_1) 对 (b_1) 取或, (a_2) 对 (b_2) 取或即可。
最终该询问 (0/1) 都可以的位置的个数即为 (a_1) 中 (1) 的个数。
时间复杂度 (O(mq)),期望得分 (15~pts)
子任务 (5):
由于 (n) 只有 (1),问题变成了求某个区间内的字符是不是全是 0,全是 1,全是 ? 或 0 和 1 都有。可以考虑用线段树非常轻松的维护这样的信息。
时间复杂度 (O(q log m)),期望得分 (15~pts)
子任务 (6):
世界上没有什么事情是开一棵线段树不能解决的,如果有,那就开 (30) 棵。
时间复杂度 (O(nq log m)),期望得分 (10~pts)
子任务 (7):
考虑结合子任务 (4) 和子任务 (5) 的做法,发现两个区间的状压信息也可以用子任务 (4) 的方法合并。因此用线段树维护这两个 int 的状压信息即可。
时间复杂度 (O(q log m)),期望得分 (30~pts)