【ML-4】逻辑回归--用于分类

目录

1. 简述
2. 二元逻辑回归的模型
3. 二元逻辑回归的损失函数及推导
4. 二元逻辑回归的正则化
5. 二元逻辑回归的推广：多元逻辑回归
6. 总结

一、简述

逻辑回归是一个分类算法（区别与线性回归），它可以处理二元分类以及多元分类。虽然它名字里面有"回归"两个字，却不是一个回归算法。那为什么有"回归"这个误导性的词呢？个人认为，虽然逻辑回归是分类模型，但是它的原理里面却残留着回归模型的影子。

前奏：

用一句话概括：逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

1.1 从线性回归到逻辑回归

我们知道，线性回归的模型是求出输出特征向量Y和输入样本矩阵X之间的线性关系系数θ，满足Y=Xθ。此时我们的Y是连续的，所以是回归模型。

如果我们想要Y是离散的话，怎么办呢？一个可以想到的办法是，我们对于这个Y再做一次函数转换，变为g(Y)。如果我们令g(Y)的值在某个实数区间的时候是类别A，在另一个实数区间的时候是类别B，以此类推，就得到了一个分类模型。如果结果的类别只有两种，那么就是一个二元分类模型了。逻辑回归的出发点就是从这来的。下面我们开始引入二元逻辑回归。

二、二元逻辑回归的模型

上一节我们提到对线性回归的结果做一个在函数g上的转换，可以变化为逻辑回归。这个函数g在逻辑回归中我们一般取为sigmoid函数，形式如下：

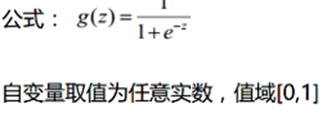
它有一个非常好的性质，即当z趋于正无穷时，g(z)趋于1，而当z趋于负无穷时，g(z)趋于0，这非常适合于我们的分类概率模型。另外，它还有一个很好的导数性质：

g′(z)=g(z)(1−g(z))

这个通过函数对g(z)求导很容易得到，后面我们会用这个式子。

如果我们令g(z)中的z为：z=xθ，这样就得到了二元逻辑回归模型的一般形式：

则逻辑回归输出的预测函数数学表达式为

   

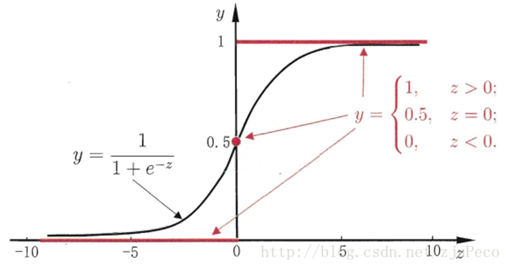
将任意的数字映射到（0，1）区间。即线性变换中的任意一个值，都可以映射到sigmoid函数中完成由值到概率的转换，从而达到分类的目的

三、二元逻辑回归的损失函数及推导

回顾下线性回归的损失函数，由于线性回归是连续的，所以可以使用模型误差的的平方和来定义损失函数。但是逻辑回归不是连续的，自然线性回归损失函数定义的经验就用不上了。不过我们可以用最大似然法来推导出我们的损失函数。

我们知道，按照第二节二元逻辑回归的定义，假设我们的样本输出是0或者1两类。那么我们有：

把这两个式子写成一个式子，就是：

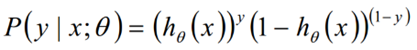
其中y的取值只能是0或者1。得到了y的概率分布函数表达式，我们就可以用似然函数最大化来求解我们需要的模型系数θ。

为了方便求解，这里我们用对数似然函数最大化。其中：似然函数的代数表达式为：

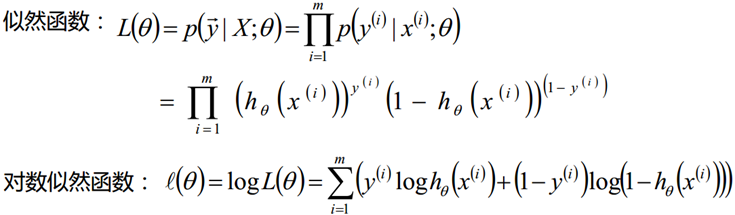
其中m为样本的个数。对于二元逻辑回归的损失函数极小化，有比较多的方法，最常见的有梯度下降法，坐标轴下降法，等牛顿法等。这里推导出梯度下降法中θ每次迭代的公式。

对数似然函数取反即为我们的损失函数J(θ)

代数求导方法：

求解(通过参数的变化得到最优解)：

本公式使用了多元回归的softmax函数。

四、二元逻辑回归的正则化

逻辑回归也会面临过拟合问题，所以我们也要考虑正则化。常见的有L1正则化和L2正则化。

逻辑回归的L1正则化的损失函数表达式如下，相比普通的逻辑回归损失函数，增加了L1的范数做作为惩罚，超参数α作为惩罚系数，调节惩罚项的大小:

二元逻辑回归的L1正则化损失函数表达式如下：

逻辑回归的L1正则化损失函数的优化方法常用的有坐标轴下降法和最小角回归法。

二元逻辑回归的L2正则化损失函数表达式如下：

逻辑回归的L2正则化损失函数的优化方法和普通的逻辑回归类似。

五、二元逻辑回归的推广：多元逻辑回归

前面几节我们的逻辑回归的模型和损失函数都局限于二元逻辑回归，实际上二元逻辑回归的模型和损失函数很容易推广到多元逻辑回归。比如总是认为某种类型为正值，其余为0值，这种方法为最常用的one-vs-rest，简称OvR.

另一种多元逻辑回归的方法是Many-vs-Many(MvM)，它会选择一部分类别的样本和另一部分类别的样本来做逻辑回归二分类。最常用的是One-Vs-One（OvO）。OvO是MvM的特例。每次我们选择两类样本来做二元逻辑回归。

这里只介绍多元逻辑回归的softmax回归的一种特例推导：

如果我们要推广到多元逻辑回归，则模型要稍微做下扩展。

我们假设是K元分类模型,即样本输出y的取值为1，2，。。。，K。

解出这个K元一次方程组，得到K元逻辑回归的概率分布如下：

多元逻辑回归的损失函数推导以及优化方法和二元逻辑回归类似，这里就不累述。

六、总结

逻辑回归尤其是二元逻辑回归是非常常见的模型，训练速度很快，虽然使用起来没有支持向量机（SVM）那么占主流，但是解决普通的分类问题是足够了，训练速度也比起SVM要快不少。如果你要理解机器学习分类算法，那么第一个应该学习的分类算法个人觉得应该是逻辑回归。理解了逻辑回归，其他的分类算法再学习起来应该没有那么难了。

优点：

1. 形式简单，模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大。
2. 模型效果不错。在工程上是可以接受的（作为baseline)，如果特征工程做的好，效果不会太差，并且特征工程可以大家并行开发，大大加快开发的速度。
3. 训练速度较快。分类的时候，计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟，训练的速度可以通过堆机器进一步提高，这样我们可以在短时间内迭代好几个版本的模型。
4. 资源占用小,尤其是内存。因为只需要存储各个维度的特征值，。
5. 方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果，因为输出的是每个样本的概率分数，我们可以很容易的对这些概率分数进行cutoff，也就是划分阈值(大于某个阈值的是一类，小于某个阈值的是一类)。

缺点:

1. 准确率并不是很高。因为形式非常的简单(非常类似线性模型)，很难去拟合数据的真实分布。
2. 很难处理数据不平衡的问题。举个例子：如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器，它对正负样本的区分能力不会很好。
3. 处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下，只能处理线性可分的数据，或者进一步说，处理二分类的问题 。
4. 逻辑回归本身无法筛选特征。有时候，我们会用gbdt来筛选特征，然后再上逻辑回归。

逻辑回归函数参数说明：https://blog.csdn.net/jark_/article/details/78342644

   

一般问题：

（1）线性回归这边比较重要的误差以及与误差相关的似然函数是怎么理解的？

回答：误差一般都是用均方误差或者绝对值误差来衡量。至于似然函数，个人觉得可以简单理解是损失函数的对立面。即如果损失函数是要最小化f(x),则似然函数就是最大化−f(x)。当然只有部分算法的损失函数和似然函数能满足这样的关系。

（2）范式的作用和解释：

（3）由于该极大似然函数无法直接求解，我们一般通过对该函数进行梯度下降来不断逼急最优解。在这个地方其实会有个加分的项，考察你对其他优化方法的了解。因为就梯度下降本身来看的话就有随机梯度下降，批梯度下降，small batch 梯度下降三种方式，面试官可能会问这三种方式的优劣以及如何选择最合适的梯度下降方式。

答：

1.简单来说 批梯度下降会获得全局最优解，缺点是在更新每个参数的时候需要遍历所有的数据，计算量会很大，并且会有很多的冗余计算，导致的结果是当数据量大的时候，每个参数的更新都会很慢。

2.随机梯度下降是以高方差频繁更新，优点是使得sgd会跳到新的和潜在更好的局部最优解，缺点是使得收敛到局部最优解的过程更加的复杂。

3.小批量梯度下降结合了sgd和batch gd的优点，每次更新的时候使用n个样本。减少了参数更新的次数，可以达到更加稳定收敛结果，一般在深度学习当中我们采用这种方法。

--其实这里还有一个隐藏的更加深的加分项，看你了不了解诸如Adam，动量法等优化方法。因为上述方法其实还有两个致命的问题。

1.第一个是如何对模型选择合适的学习率。自始至终保持同样的学习率其实不太合适。因为一开始参数刚刚开始学习的时候，此时的参数和最优解隔的比较远，需要保持一个较大的学习率尽快逼近最优解。但是学习到后面的时候，参数和最优解已经隔的比较近了，你还保持最初的学习率，容易越过最优点，在最优点附近来回振荡，通俗一点说，就很容易学过头了，跑偏了。

2.第二个是如何对参数选择合适的学习率。在实践中，对每个参数都保持的同样的学习率也是很不合理的。有些参数更新频繁，那么学习率可以适当小一点。有些参数更新缓慢，那么学习率就应该大一点。这里我们不展开，有空我会专门出一个专题介绍。

附件一：手写推导过程练习

   

参考文档：

https://www.cnblogs.com/pinard/p/6029432.html

https://www.cnblogs.com/ModifyRong/p/7739955.html