pointcnn

这篇论文先举例子解释了为什么卷积无法直接应用在点云数据上。

 

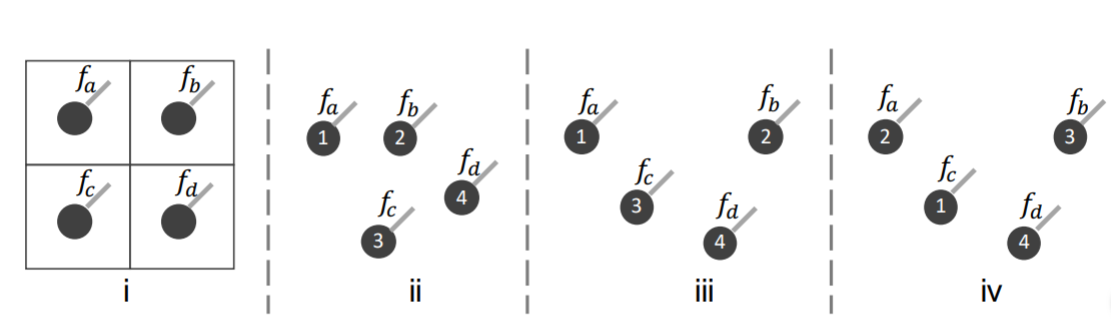
如图1， 传统的卷积是作用在2维图像数据上。图像中每个像素的顺序是固定的，也就是说数据是结构化存储的。直接使用conv2d就能从这种潜在的空间结构中获取信息。

而点云数据是点集，如果直接使用卷积会出现图中234多种情况

        

    若直接使用卷积，则f2与f3的计算结果是相等的，但是从图中可知，23显示不同，这说明卷积无法获得点的空间信息

    而f3与f4的计算结果不等，但是图3与图4是相同的点集，必须得到相同的计算结果才合理，这说明卷积无法适应点集的N！种排列。

    在其他论文里，为了适应点云数据的这两种的特点采取的方式有体素化、3DCNN及PointNet提的对称操作（symmetric，这个翻译是我自己译的）
版权声明：本文为CSDN博主「Link2Link」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_15602569/article/details/79560614

---

卷积神经网络（Conv）能够很好利用原始数据的在空间上的局部相关性(Spatially-local correlation),这也正是卷积神经网络在各种分割或者分类任务中取得成功的关键。正是如此，作者设想是否能效仿卷积神经网络来很好的利用点云(Point Cloud)的空间上的局部相关性，这将在点云分割和分类上取得很大的成功。所以这篇文章的重点就在于怎么利用这种相关性。
版权声明：本文为CSDN博主「JMU-HSF」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_42956785/article/details/86586513

---

首先，根据采样得到的中心点，将全局坐标变为局部坐标，相当于分区。（点的数量如何确定?)

o 利用MLP将每个点变换到高维空间（一维卷积），得到F-sigma

o Concat特征F（输入的每个点的附加特征，比如color或者normal）和F-sigma,得到新的特征F*

o 对每个局部区域中的点使用MLP，得到变换矩阵X。这里可以注意一下，得到变换矩阵X的过程，输入是P'（一组坐标点），输出是变换矩阵X。文中的消除实验表明，X变换的确是有效果的

o 对特征F*使用X进行变换后，在进行传统的卷积（1维)。作者是希望通过X变换，把特征F*变成空间相关，也就是希望矩阵中相邻的在空间中也相邻，这样就可以像图像一样卷积了。

最后的Conv是一维卷积。可以看到X-Conv中所用的都还是一维卷积，不管是MLP还是Conv，作者在论文的脚注部分也提到了，代码中也可以确认这一点。所以，作者用CNN做类比还是不太合适，唯一的共同点是尺寸的点的数量是由多变少，CNN中图像尺寸也是由大到小

o 一个区域的点是怎么变成一个中心点的特征的？在PointNet++中，作者是对每一个局部区域进行Maxpool得到一个一维的向量作为中心点的特征，在pointCNN中并没有使用maxpool。在本文中，最后一步使用了（1，K)的卷积核进行卷积，对每个区域中不同点的特征进行了融合，而在pointnet中，这一步是通过每个点对应维数的最大值，个人觉得，这是两者之间最大的不同，可能也是导致结果差别的主要原因，但这只是猜测，后续还需要进行实验验证。在这一一步中，为了减少参数量，作者使用了深度可分离卷积，

作者：摸鱼家
链接：https://zhuanlan.zhihu.com/p/89752154
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

---

 https://blog.csdn.net/qq_33278989/article/details/80047252