leetcode刷题之动态规划

leetcode刷题之动态规划

下面是7、8月份总结的一些关于动态规划刷题的一些问题。

子串和子序列问题

首先是子串和子序列
子串的话就是要连续的，子序列的话可以不用连续，这里都是可以使用动态规划来完成
Abcd--ab是子串，子序列可以是ac
给出abcde和abdi
1. 第一种是问最长公共子序列是多少，输出
2. 第二种是问最长公共子串是多少，输出

公共子序列

公共子串

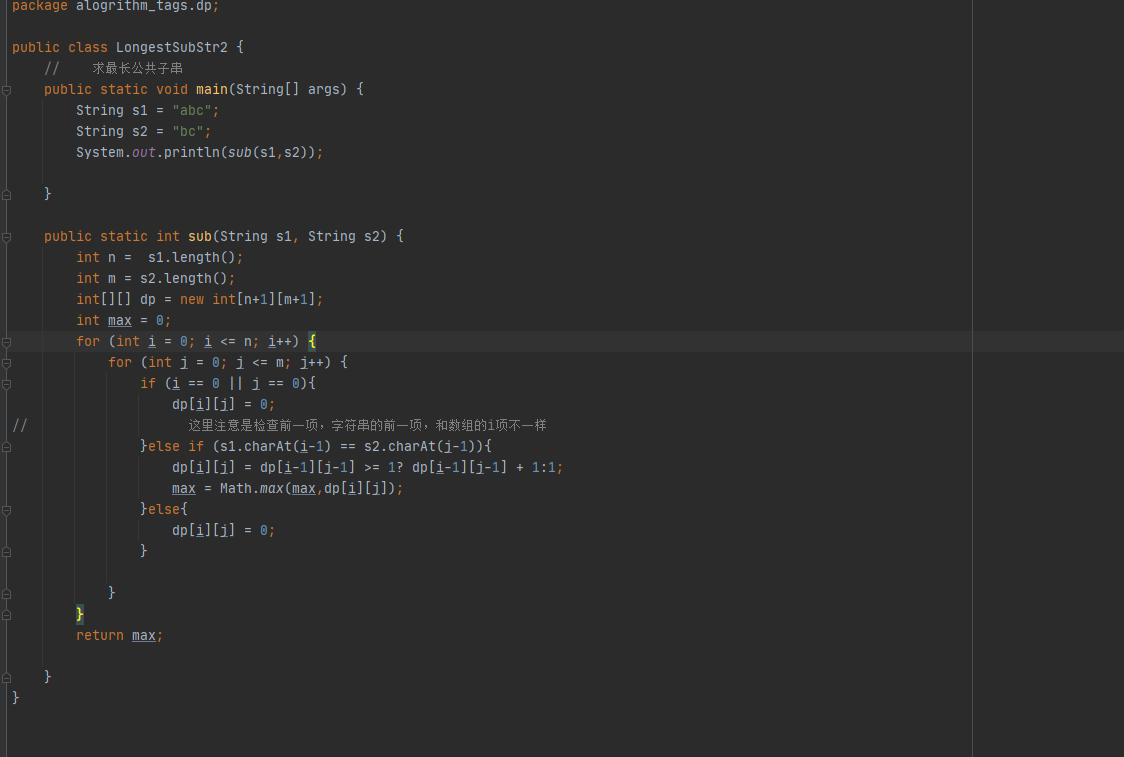
至少有k个重复字符的最长子串问题

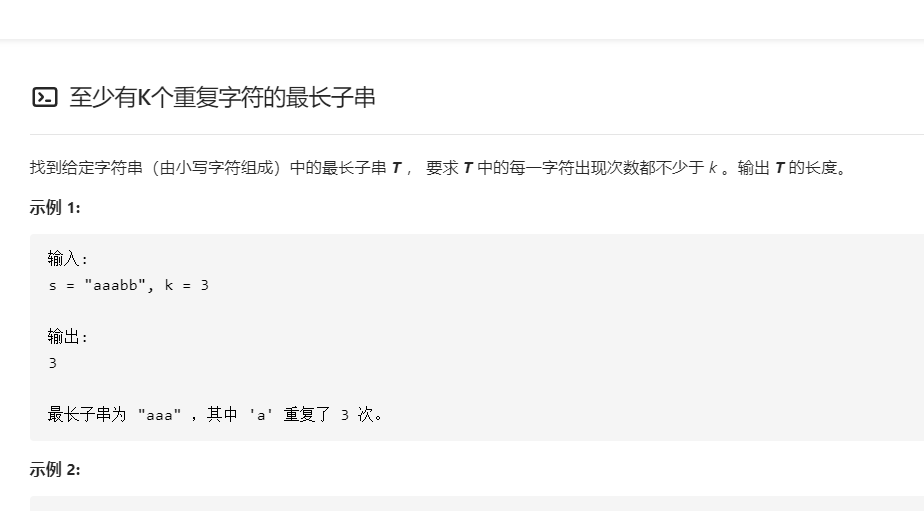
这个问题还有递归解决的方法。

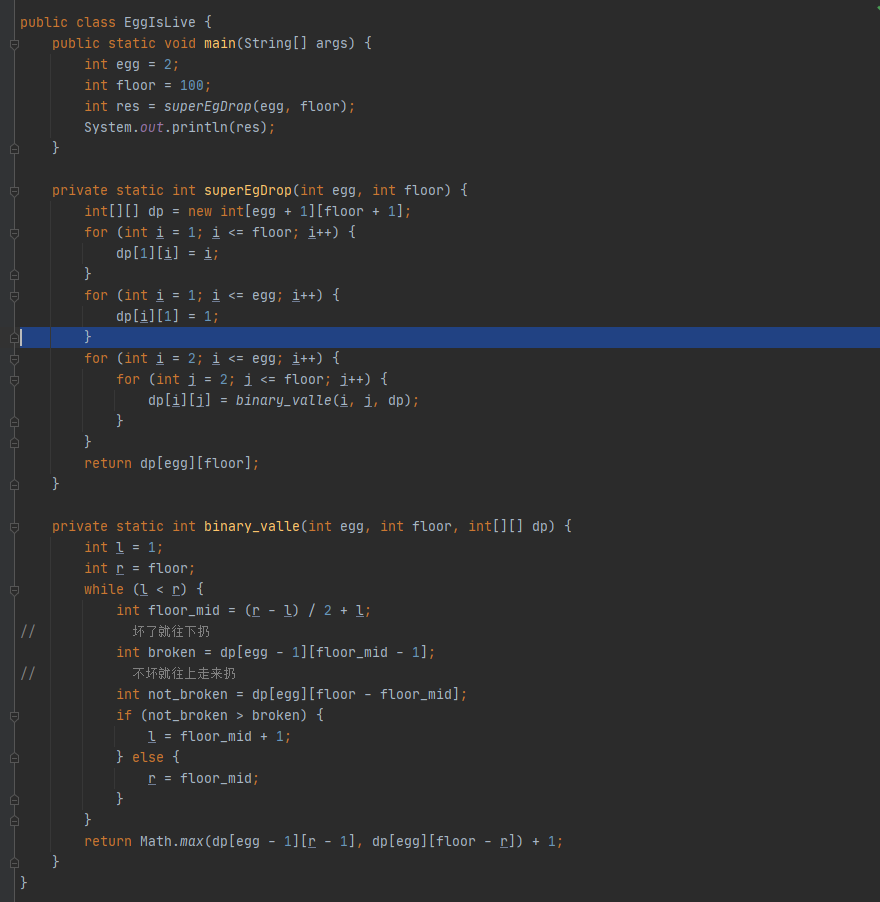
高楼扔鸡蛋

这个问题是n层楼，扔鸡蛋，怎么用至少的次数找到鸡蛋的临界点（在某层楼扔下来，刚刚好不碎）
可以使用动态规划+二分查找
定义好鸡蛋碎与没碎

Version1

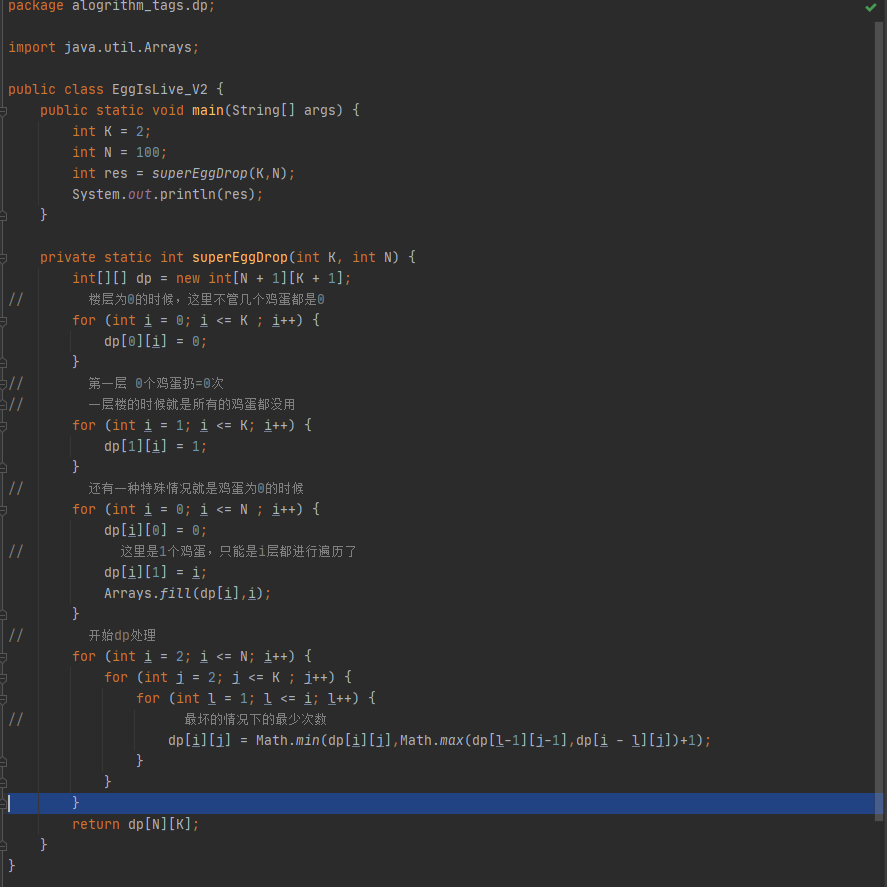
Version2

动态规划之网格路径

1.leetcode64-最小路径和

思路：这里重点解决在左边界和上边界的值先，然后任何一点的最小值，都要用i-1和j-1的值取最小值。

//特殊情况处理
 for(int i = 1; i < row; i++){
            grid[i][0] += grid[i-1][0];
        }
for(int i = 1; i < col; i++){
            grid[0][i] += grid[0][i-1];
        }

//状态转移方程
	dp[i][j] = dp[i][j] + Math.min(grid[i-1][j],grid[i][j-1]);

所以这道题而言，其实是可以很快解决的。

c++代码如下

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        for(int i = 1; i < row; i++){
            grid[i][0] += grid[i-1][0];
        }
        for(int i = 1; i < col; i++){
            grid[0][i] += grid[0][i-1];
        }
        for(int i = 1; i < row; i++){
            for(int j = 1; j < col; j++){
                grid[i][j] += min(grid[i-1][j],grid[i][j-1]);
            }
        }
        return grid[row-1][col-1];

        
    }
};

java代码如下

class Solution {
    public int minPathSum(int[][] grid) {
        // 使用动态规划
        int row = grid.length;
        int col = grid[0].length;
        if(row == 0 || col == 0) return 0;
        for(int i = 1; i < row; i++){
            grid[i][0] += grid[i-1][0];
        }
         for(int i = 1; i < col; i++){
            grid[0][i] += grid[0][i-1];
        }
         for(int i = 1; i < row; i++){
             for(int j = 1; j < col; j++){
                 grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);
             }
        }
        return grid[row-1][col-1];
    }
}

2.拓展题--类似的：避过某些点的路径总和

一个办公室非常大，小虾同学的位置坐落在右上角，而大门却在左下角，可以把所有位置抽象为一个网格（门口的坐标为0，0），小虾同学很聪明，每次只向上，或者向右走，因为这样最容易接近目的地，但是小虾同学不想让自己的boss们看到自己经常在他们面前出没，或者迟到被发现。他决定研究一下如果他不通过boss们的位置，他可以有多少种走法？*

简单讲就是从网盘的一边走到另一边，中途不能走某些点，求走法有几种？

思路：这里要将boss也就是不能走的点进行标记，可以设置为某个值，比如-1，然后双层for遍历的时候，就continue跳过该值

这里和上面的题一样，处理特殊情况时候，要注意先看边界，在这道题，也就是只能是一种走法的边。

//特殊情况
for(int i = 0; i <= x; i++){
	dp[0][i] = 1;//也就是第一行，最下的一层位置，只能是一种走法，一直往右走
}
for(int i = 0; i <= y; i++){
	dp[i][0] = 1;//也就是左侧第一列，最左的一层位置，只能是一种走法，一直往上走
}

import java.util.Scanner;

public class pathSum {
    public static void main(String[] args) {
        //查找
        //利用动态规划来做
        Scanner sc = new Scanner(System.in);
        int ax = sc.nextInt();
        int ay = sc.nextInt();
        int num = sc.nextInt();
//        注意这里会爆数据范围，要使用更大的数据范围
        long[][] dp = new long[ax+1][ay+1];
        for (int i = 0; i < num; i++) {
            int x = sc.nextInt();
            int y = sc.nextInt();
            dp[x][y] = -1;
        }
        for (int i = 0; i <= ax; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i <= ay; i++) {
            dp[0][i] = 1;
        }
        for (int i = 1; i <= ax; i++) {
            for (int j = 1; j <= ay ; j++) {
                //boss位置直接跳过
                if (dp[i][j] == -1) continue;
//                分开判定，有遇到boss位置就躲
                if (dp[i-1][j] != -1  ) {
                    dp[i][j] +=   dp[i-1][j];
                }
                if (dp[i][j -1] != -1  ) {
                    dp[i][j] +=  dp[i][j - 1];
                }
            }
        }
        System.out.print(dp[ax][ay]);
    }
}

}