我们知道了二叉树的递归遍历,在理解了递归的过程后,二叉树的遍历就觉得很简单。但是非递归的遍历帮我更好的理解栈的应用和二叉树的遍历。
~~~~~先序遍历非递归算法
由先序遍历可知,遍历时先访问根结点,再遍历左子树,最后遍历右子树。根的指针域指向左右子树,因此访问左子树时不会丢失右子树的地址。所以,非递归需要一个栈来保存左右子树的地址。
栈,先进后出,所以当访问完一个非叶子结点后,应该将其右孩子进栈。再将左孩子进栈。
思路->
将根结点b进栈
while(栈不空)
{
出栈结点p并访问它;
若p有右孩子,右孩子进栈;
若p有左孩子,左孩子进栈
}
具体代码->(顺序栈)
void PreOrder(BTNode *b)
{
BTNode *st[MaxSize];
BTNode *p;
int top = -1;
if(b != NULL)
{
top ++;//根结点进栈
st[top] = b;
while(top > -1)//不为空循环
{
p = st[top];
top--;
cout<<p->data;//退栈并访问
if(p->rchild != NULL)//有右孩子,进栈
{
top++;
st[top] = p->rchild;
}
if(p->lchild != NULL)//有左孩子,进栈
{
top++;
st[top] = p->lchild;
}
}
cout<<endl;
}
}
~~~~~中序遍历非递归算法
中序,遍历顺序为左根右,在先序遍历非递归算法的基础上修改,需要将根结点及其左下结点依次进栈但不访问,因为左子树还没有遍历。当到达根结点的最左下结点时,就是中序遍历的开始结点,即栈顶结点,出栈并访问,然后转向右子树,重复上述过程
思路->
p = b;
while(栈不为空或p!=NULL)
{
while(结点p有左孩子)
{
将p进栈;
p = p->lchild;
}
//此时栈顶结点(尚未访问)无左孩子或左孩子已遍历过
if(栈不为空)
{
出栈p并访问;
p = p->rchild;
}
}
具体代码->
void InOrder(BTNode *b)
{
BTNode *st[MaxSize];
BTNode *p;
int top = -1;
if( b != NULL)
{
p = b;
while(top > -1 || p != NULL)
{
while( p!= NULL)//p的所有左下结点进栈 不访问
{
top++;
st[top] = p;
p = p->lchild;
}
if(top > -1)
{
p = st[top];//出栈p并访问
top--;
cout<<p->data;
p = p->rchild;
}
}
cout<<endl;
}
}
~~~~~后序遍历非递归算法
后续遍历,为左右根。非递归遍历先将很结点及其左下结点依次进栈,即在栈顶结点p的左子树已遍历或为空,但仍不访问结点p,因为右子树没有遍历,只有右子树已遍历完才能访问结点p。
思路->
p = b;
do
{
while(结点p有左孩子)
{
将结点p进栈;
p = p->lchild;
}
//此时栈顶结点(尚未访问)没有左孩子或已遍历过
while(栈不为空且p为栈顶结点)
{
取栈顶结点p;
if(结点p的右子树已访问)
{
访问结点p;
退栈;
}
else
p = p->rchild;
}
}while(栈不为空)
注意!! 这里需要解决两个问题:
1.如何判断当前处理的结点p是栈顶结点,为此可以设置一个flag,在do-while循环中第一个while结束后开始处理栈顶结点,置flag为true;一旦转向处理右子树,flag为false。
2.如何判断p的右子树已遍历过。在一颗二叉树中,任何一颗空子树的后续遍历序列中最后访问的一定是该子树的根结点,因此,若结点p的右孩子刚访问过,则它的右子树已遍历完,可以访问p了。当然,结点p的右孩子为空,也可以访问p。为此设置一个指针变量r,初值为NULL,指向刚刚访问过的结点。对于正在处理的栈顶结点p,一旦p->rchild ==r,说明p的左右子树都遍历过了,可以访问p了。
具体代码->
void PostOrder(BTNode *b)
{
BTNode *st[MaxSize];
BTNode *p;
int top = -1;
bool flag;//栈指针初值
if(b != NULL)
{
do
{
while(b != NULL)//b所有左下结点进栈
{
top++;
st[top] = b;
b = b->lchild;
}
p = NULL;//p指向当前结点的上一个已经访问的结点
flag = true;
while(top != -1 && flag)//flag为真表示正在处理栈顶结点
{
b = st[top];//取出栈顶结点
if(b->rchild == p)//右子树不存在或已被访问。访问
{
cout<<b->data;//访问b
top--;
p = b;//p指向已被访问结点
}
elel
{
b = b->rchild;
flag = false;//当前处理的不是栈顶结点
}
}
}while(top != -1);
cout<<endl;
}
}
~~~~~以下为完整代码
#include<iostream>
#include<stdio.h>
#include<malloc.h>
using namespace std;
#define ElemType char
#define MaxSize 100
typedef struct node
{
ElemType data;
struct node *lchild;
struct node *rchild;
}BTNode;
void CreateBTree(BTNode *&b)//手动输入二叉树
{
b = NULL;
char ch;
ch = getchar();
if(ch == '#')
{
b = NULL;
}
else
{
b = (BTNode *)malloc(sizeof(BTNode));
b->data = ch;
CreateBTree(b->lchild);
CreateBTree(b->rchild);
}
}
void DispLeaf(BTNode *b)//Print All Leaf
{
if(b != NULL)
{
if(b->lchild == NULL && b->rchild == NULL)
{
cout<<b->data;
}
DispLeaf(b->lchild);//lchild leaf
DispLeaf(b->rchild);//rhcild leaf
}
}
BTNode* FindNode(BTNode *b,ElemType x)//return a Node
{
BTNode *p;
if(b == NULL)
{
return NULL;
}
else if(b->data == x)
{
return b;
}
else
{
p = FindNode(b->lchild,x);
if(p != NULL)
{
return p;
}
else
{
return FindNode(b->rchild,x);
}
}
}
BTNode* LchildNode(BTNode *p)//return p lchild
{
return p->lchild;
}
BTNode* RchildNode(BTNode *p)//return p rchild
{
return p->rchild;
}
int BTHeight(BTNode *b)//return BTheigh
{
int lchildh,rchildh;
if(b == NULL)
{
return (0);
}
else
{
lchildh = BTHeight(b->lchild);
rchildh = BTHeight(b->rchild);
return (lchildh >rchildh) ? (lchildh + 1): (rchildh + 1);
}
}
int Level(BTNode *b,ElemType x,int h)//return Level
{
int level;
if(b == NULL)
{
return (0);
}
else if(b->data == x)
{
return h;
}
else
{
level = Level(b->lchild,x,h+1);
if(level != 0)
{
return level;
}
else
{
return (Level(b->rchild,x,h+1));
}
}
}
void DispBTree(BTNode *b)
{
if(b != NULL)
{
cout<<" "<<b->data;
if(b->lchild != NULL || b->rchild != NULL)
{
cout<<"(";//有孩子结点才输出(
DispBTree(b->lchild);//扫描左子树
if(b->rchild != NULL)//有右子树才输出,
{
cout<<",";
}
DispBTree(b->rchild);//递归处理右子树
cout<<")";//有孩子结点才输出
}
}
}
void PreOrder(BTNode *b)
{
BTNode *st[MaxSize];
BTNode *p;
int top = -1;
if(b != NULL)
{
top ++;//根结点进栈
st[top] = b;
while(top > -1)//不为空循环
{
p = st[top];
top--;
cout<<p->data;//退栈并访问
if(p->rchild != NULL)//有右孩子,进栈
{
top++;
st[top] = p->rchild;
}
if(p->lchild != NULL)//有左孩子,进栈
{
top++;
st[top] = p->lchild;
}
}
cout<<endl;
}
}
void InOrder(BTNode *b)
{
BTNode *st[MaxSize];
BTNode *p;
int top = -1;
if( b != NULL)
{
p = b;
while(top > -1 || p != NULL)
{
while( p!= NULL)//p的所有左下结点进栈 不访问
{
top++;
st[top] = p;
p = p->lchild;
}
if(top > -1)
{
p = st[top];//出栈p并访问
top--;
cout<<p->data;
p = p->rchild;
}
}
cout<<endl;
}
}
void PostOrder(BTNode *b)
{
BTNode *st[MaxSize];
BTNode *p;
int top = -1;
bool flag;//栈指针初值
if(b != NULL)
{
do
{
while(b != NULL)//b所有左下结点进栈
{
top++;
st[top] = b;
b = b->lchild;
}
p = NULL;//p指向当前结点的上一个已经访问的结点
flag = true;
while(top != -1 && flag)//flag为真表示正在处理栈顶结点
{
b = st[top];//取出栈顶结点
if(b->rchild == p)//右子树不存在或已被访问。访问
{
cout<<b->data;//访问b
top--;
p = b;//p指向已被访问结点
}
else
{
b = b->rchild;
flag = false;//当前处理的不是栈顶结点
}
}
}while(top != -1);
cout<<endl;
}
}
void DestoryBTree(BTNode *&b)
{
if(b != NULL)
{
DestoryBTree(b->lchild);
DestoryBTree(b->rchild);
free(b);
}
}
int main()
{
BTNode *b;
cout<<"Create "<<endl;
CreateBTree(b);
cout<<"BTree Height is "<< BTHeight(b)<<endl;
//~~~~Order!~~~
cout<<"非递归先序遍历 -> ";
PreOrder(b);
cout<<endl;
cout<<"非递归中序遍历 -> ";
InOrder(b);
cout<<endl;
cout<<"非递归后序遍历 -> ";
PostOrder(b);
cout<<endl;
cout<<"Leaf Node-> ";
DispLeaf(b);
cout<<endl;
cout<<"C level is:"<<Level(b,'C',1)<<endl;
cout<<"Free"<<endl;
DestoryBTree(b);
return 1;
}
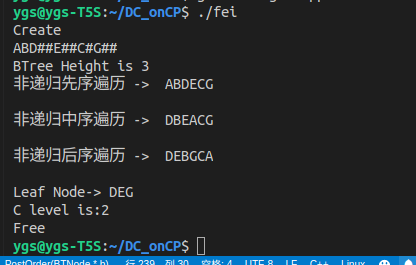
~~~~~运行结果为: