POJ1988(Cube Stacking)--并查集

题目链接：http://poj.org/problem?id=1988

题意：有n个元素，开始每个元素各自在一个栈中，有两种操作，将含有元素x的栈放在含有y的栈的顶端，合并为一个栈。

第二种操作是询问含有x元素下面有多少个元素。

思路：

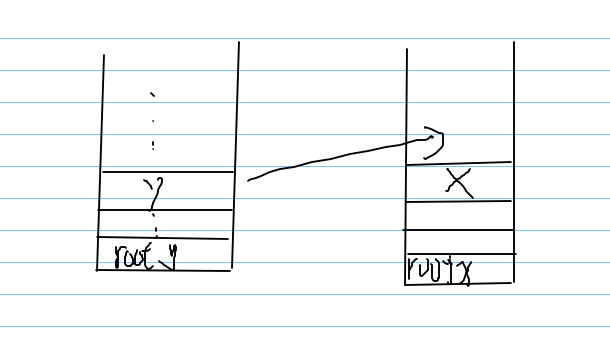
并查集，把每一堆看作一个栈，堆的下方看作栈顶。因为当我们知道栈中元素的总数，和某元素到“栈顶”的距离，

我们就能知道这个元素下面有多少元素。合并操作的时候，始终使用在下面栈的根来做合并之后的根，这样也就达到了栈中的根是栈中的“栈顶”元素的效果，我们只需在每个“栈顶”中记录该栈中的元素总数即可。然而我们还需要得知某元素到“栈顶”的距离，这样我们就需要记录每个元素到其父亲的距离，把它到根上所经过的距离加起来，即为它到“栈顶”的距离。这样我们就得出了结果。

 

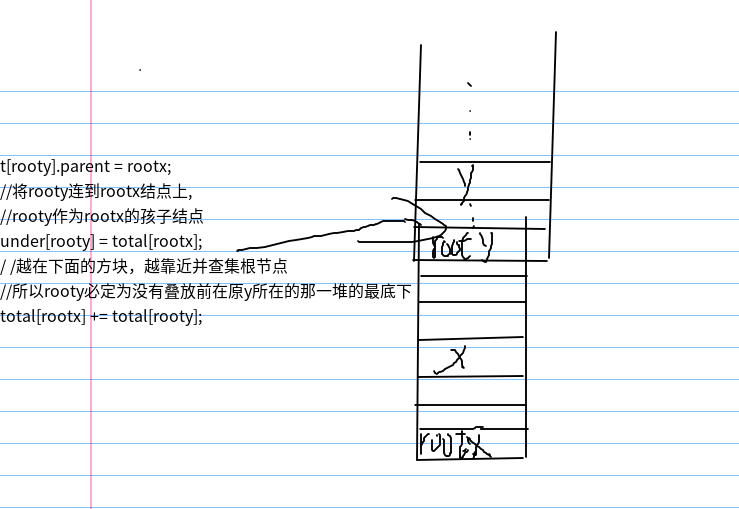
这个图是在合并的时候的关键部分 

另外，在进行Find()操作时，有一句 under[x] += under[t[x].parent];这句话就是在递归寻找根结点时，计算出每个元素距离栈底（根）的距离。

#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cmath>
#include<vector>
#include<stack>
#include<map>
#include<set>
#include<list>
#include<queue>
#include<string>
#include<algorithm>
#include<iomanip>
using namespace std;

struct node
{
    int parent;
    int date;
};

int * total;
int * under;

class DisJoinSet
{
protected:
    int n;
    
    node * tree;
public:
    DisJoinSet(int n);
    ~DisJoinSet();
    void Init();
    int Find(int x);
    void Union(int x,int y);
};

DisJoinSet::DisJoinSet(int n)
{
    this->n = n;
    tree = new node[n+2];
    total = new int[n+2];
    under = new int[n+2];
    Init();
}
DisJoinSet::~DisJoinSet()
{
    delete[] under;
    delete[] total;
    delete[] tree;
}

void DisJoinSet::Init()
{
    for(int i = 1;i  <= n ;i ++)
    {
        tree[i].date  = i;
        tree[i].parent = i;
        total[i] = 1;
        under[i] = 0;
    }
}
int DisJoinSet::Find(int x)
{
    //int temp = tree[x].parent;
    if(x != tree[x].parent)
    {
        int par = Find(tree[x].parent);
        under[x] += under[tree[x].parent];//把父亲结点下面的个数加到自己头上
        tree[x].parent = par;
        return tree[x].parent;
    }
    else
    {
        return x;
    }
}

void DisJoinSet::Union(int x,int y)
{
    int pa = Find(x);
    int pb = Find(y);
    if(pa == pb)return ;
    else
    {
        tree[pa].parent = pb;//x的根变为y的根  即把x所在的堆放在y所在的堆上面
        under[pa] = total[pb];//pa下的数量即原来y所在栈里的元素total
        total[pb] += total[pa];//更新y的totoal
    }
}

int main()
{
    int p;
    while(scanf("%d",&p) != EOF)
    {
        if(p == 0)break;
        DisJoinSet dis(p);
        char s1[2];
        for(int i = 0 ;i < p ;i++)
        {
            
            int s2;
            int s3;
            scanf("%s",s1);
            if(s1[0] == 'M')
            {
                scanf("%d%d",&s2,&s3);
                int pa = dis.Find(s2);
                int pb = dis.Find(s3);
                if(pa != pb)
                {
                    dis.Union(s2,s3);
                }
            }
            if(s1[0] == 'C')
            {
                scanf("%d",&s2);
                dis.Find(s2);
                cout<<under[s2]<<endl;
            }
        }
        dis.~DisJoinSet();
    }
    return 0;
}