前序
由于比赛地址是在计蒜客,所以本篇题解省略题的详细地址,只给出比赛地址,对于题目有兴趣的可以点击下方链接
比赛地址
A. 盘他!
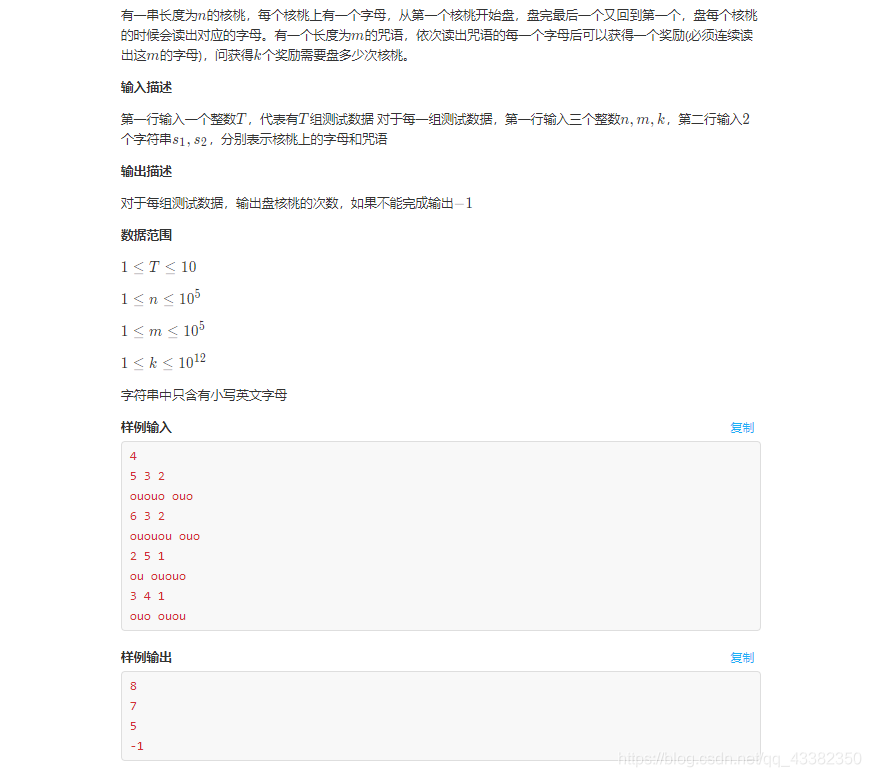
截图
题目类型
字符串模拟
题意简述
求解子串在首尾可以无线相接的母串中不重叠出现k次,需要经过多少个字符(从头开始计算)
题解
本题的解答概括为两个部分,
- 第一个部分是KMP匹配
- 第二个部分是寻找循环节
kmp匹配的目的是为了判断是否有可能存在不重叠出现k次的情况,并且为寻找循环节和最后位置提供机会
这里先给出题中样例,并进行一些解释
输入样例
5 3 2
ououo ouo
输出样例
8
5 表示单一母串长度
3 表示子串长度
2 表示子串不重叠出现次数
经过头尾链接子串出现 2 次的情况是如下
ououo ououo
通过取余的方式解决头尾无限相接的问题,这样就可以正常的进行KMP匹配惹
代码
const int MAXN=2e5+50;
int nex[MAXN];
int next_start[MAXN];
int start[MAXN];
int first_visit[MAXN];
LL first_visit_ans[MAXN];
//获取母串的next数组
void get_next(string P){
//memset(nex, 0, sizeof(nex));
int len = P.size();
nex[0] = -1;
int i = 0, j = -1;
while(i < len){
if (j == -1 || P[i] == P[j]) nex[++i] = ++j;
else j = nex[j];
}
}
int KMP(string P, string T){
int Plen = P.size();
int Tlen = T.size();
//cout << "Plen " << Plen << " " << "Tlen " << Tlen << '
';
int i = 0, j = 0;
int sum = 0;
//%Tlen就能够枚举所有的起始点,即使是超过了,也能回到想要的位置
while(i - Plen < Tlen - 1){
if (j == -1 || P[j] == T[i % Tlen]) i++, j++;
else j = nex[j];
if (j == Plen) start[sum++] = i - Tlen,j = nex[j];
//这里是对寻找到的位置返回记录匹配成功的第一个点,通过start数组就能找到所有寻找到的匹配成功的位置
}
return sum; // 查找到的匹配成功的个数
}
int main(){
int t; RD(t);
FOR_1(e, 1, t){
int n, m, k; RD(n, m, k);
string s1, s2; cin >> s1 >> s2;
get_next(s2);
int num = KMP(s2, s1);
int x, flag, round;LL ans = 0;
if (num == 0) {
OT("-1");
continue;
}//一个匹配都没找到
for(int i = 0;i < s1.size(); i++){
next_start[i] = -1;
first_visit[i] = -1;
}
for(int i = 0; i < num; i++){
next_start[start[i]] = start[i];
}
x = -1;
for(int i = n * 2 - 1; i >= 0; i--){
if (next_start[i % n] != -1) x = next_start[i % n];
else next_start[i % n] = x;
}
x = 0, ans = 0, flag = 0; //初始化
for(LL i = 1; i <= k; i++){
ans += (next_start[x] - x + n) % n;
x = next_start[x];
if(flag == 0)
{
if(first_visit[x] != -1)
{
flag = 1;
round = i - first_visit[x]; //当前位置与出现位置的距离,即循环节
ans += ((k-i) / round) * (ans - first_visit_ans[x]);
i += (k-i)/round*round;
}
first_visit[x] = i;
first_visit_ans[x] = ans;
}
ans += m;//完整匹配的距离即为子串的长度
x = (x + m) % n;
}
printf("%lld
",ans);
}
}