Codeforces Round #277.5 (Div. 2)

题目1：

题意：问最少的交换次数。使序列不递减。且交换次数不超过n。

思路：既然不超过n。那么就使用选择排序。虽然复杂度非常高，可是交换次数确是至少的。每次找出最小值，然后和当前值交换就可以。

题目：

A. SwapSort

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

In this problem your goal is to sort an array consisting of n integers in at most n swaps. For the given array find the sequence of swaps that makes the array sorted in the non-descending order. Swaps are performed consecutively, one after another.

Note that in this problem you do not have to minimize the number of swaps — your task is to find any sequence that is no longer than n.

Input

The first line of the input contains integer n (1 ≤ n ≤ 3000) — the number of array elements. The second line contains elements of array: a0, a1, ..., an - 1 ( - 109 ≤ ai ≤ 109), where ai is the i-th element of the array. The elements are numerated from 0 to n - 1 from left to right. Some integers may appear in the array more than once.

Output

In the first line print k (0 ≤ k ≤ n) — the number of swaps. Next k lines must contain the descriptions of the k swaps, one per line. Each swap should be printed as a pair of integers i, j (0 ≤ i, j ≤ n - 1), representing the swap of elements ai and aj. You can print indices in the pairs in any order. The swaps are performed in the order they appear in the output, from the first to the last. It is allowed to print i = jand swap the same pair of elements multiple times.

If there are multiple answers, print any of them. It is guaranteed that at least one answer exists.

Sample test(s)

input

5
5 2 5 1 4

output

2
0 3
4 2

input

6
10 20 20 40 60 60

output

0

input

2
101 100

output

1
0 1

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<vector>
#include<cmath>
#include<string>
#include<queue>
#define eps 1e-9
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
priority_queue<int,vector<int>,greater<int> >Q;

const int maxn=3000+10;

int n,a[maxn];
struct Node
{
    int x,y;
}node[maxn];

int main()
{
    int cnt=0;
    while(~scanf("%d",&n))
    {
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
        for(int i=1;i<=n;i++)
        {
            int p=i;
            for(int j=i+1;j<=n;j++)
            {
                if(a[j]<a[p])
                    p=j;
            }
            if(p!=i)
            {
                node[++cnt].x=i;
                node[cnt].y=p;
                swap(a[p],a[i]);
            }
        }
        printf("%d
",cnt);
        for(int i=1;i<=cnt;i++)
            printf("%d %d
",node[i].x-1,node[i].y-1);
    }
}

题目b

题意：告诉n个男孩，和m个女孩，然后分别告诉他们跳舞的水平，然后男女可以匹配的条件是他们的水平最多相差1,。

思路：直接对他们的水平进行排列，那么就行愉快的贪心了，然后找出每一个男孩可以匹配的水平，然后从小到大选择，越小越好，由于假设选的略微大的，可能会影响后面的水平高的男孩的舞伴，所以从小到大贪是正确的。

题目：

B. BerSU Ball

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

The Berland State University is hosting a ballroom dance in celebration of its 100500-th anniversary! n boys and m girls are already busy rehearsing waltz, minuet, polonaise and quadrille moves.

We know that several boy&girl pairs are going to be invited to the ball. However, the partners' dancing skill in each pair must differ by at most one.

For each boy, we know his dancing skills. Similarly, for each girl we know her dancing skills. Write a code that can determine the largest possible number of pairs that can be formed from n boys and m girls.

Input

The first line contains an integer n (1 ≤ n ≤ 100) — the number of boys. The second line contains sequence a1, a2, ..., an (1 ≤ ai ≤ 100), where ai is the i-th boy's dancing skill.

Similarly, the third line contains an integer m (1 ≤ m ≤ 100) — the number of girls. The fourth line contains sequence b1, b2, ..., bm (1 ≤ bj ≤ 100), where bj is the j-th girl's dancing skill.

Output

Print a single number — the required maximum possible number of pairs.

Sample test(s)

input

4
1 4 6 2
5
5 1 5 7 9

output

3

input

4
1 2 3 4
4
10 11 12 13

output

0

input

5
1 1 1 1 1
3
1 2 3

output

2

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;

const int maxn=100+10;

int a[maxn],b[maxn],n,m;

bool vis[maxn];

int main()
{
    int ans,l,mid,r;
    while(~scanf("%d",&n))
    {
        ans=0;
        memset(vis,false,sizeof(vis));
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
            scanf("%d",&b[i]);
        sort(a+1,a+1+n);
        sort(b+1,b+1+m);
        for(int i=1;i<=n;i++)
        {
            l=a[i]-1,mid=a[i],r=a[i]+1;
            for(int j=1;j<=m;j++)
            {
                if(!vis[j])
                {
                    if(b[j]==l)
                    {
                        ans++;
                        vis[j]=true;
                        break;
                    }
                    else if(b[j]==mid)
                    {
                        ans++;
                        vis[j]=true;
                        break;
                    }
                    else if(b[j]==r)
                    {
                        ans++;
                        vis[j]=true;
                        break;
                    }
                }
            }
        }
        printf("%d
",ans);
    }
    return 0;
}

题目3：

题目，给出m。s。意思就是确定两个数，他们都有m位。然后每位的和加起来都是s。

思路：构造。最大值比較好求，就是从最高位向最低位选择，然后最后不满9的，下一位就是这个数，然后直接跳出来后面的全是0，在构造最小的值，最小的值首先最高位直接赋值为1。然后从最低位每位按9算，最后不足9的直接把最后的值赋给这一位。假设直到最高位还有值，那么最高位==ss+1。最小值也构造完毕。

。

ps：还要注意几个问题，首先是直接输出-1 -1的，就是s==0或者9*m<s。还有就是s==1的情况，那么直接能够用0构造，反正坑比較多。。

题目：

C. Given Length and Sum of Digits...

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You have a positive integer m and a non-negative integer s. Your task is to find the smallest and the largest of the numbers that have length m and sum of digits s. The required numbers should be non-negative integers written in the decimal base without leading zeroes.

Input

The single line of the input contains a pair of integers m, s (1 ≤ m ≤ 100, 0 ≤ s ≤ 900) — the length and the sum of the digits of the required numbers.

Output

In the output print the pair of the required non-negative integer numbers — first the minimum possible number, then — the maximum possible number. If no numbers satisfying conditions required exist, print the pair of numbers "-1 -1" (without the quotes).

Sample test(s)

input

2 15

output

69 96

input

3 0

output

-1 -1

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<vector>
#include<cmath>
#include<string>
#include<queue>
#define eps 1e-9
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
priority_queue<int,vector<int>,greater<int> >Q;

const int maxn=100+10;

int m,xx;
char s[maxn],t[maxn];


int main()
{
    int ss;
    while(~scanf("%d%d",&m,&xx))
    {
       for(int i=0;i<maxn;i++)
            s[i]='0',t[i]='0';
       if(xx==1)
       {
           printf("1");
           for(int i=1;i<m;i++)  printf("0");
           printf(" ");
           printf("1");
           for(int i=1;i<m;i++)  printf("0");
           printf("
");
       }
       else if(xx==0&&m==1)
       {
           printf("0 0
");
           continue;
       }
       else if(xx>9*m||(xx==0&&m>1))
       {
           puts("-1 -1");
           continue;
       }
       else
       {
           ss=xx;
           ss--;
           t[0]='1';
           for(int i=m-1;i>0;i--)
           {
               int x=min(ss,9);
               if(x==0)  break;
               t[i]=x+'0';
               ss-=x;
           }
           if(ss)  t[0]=ss+1+'0';
           for(int i=0;i<m;i++)
              printf("%c",t[i]);
           printf(" ");
           ss=xx;
           for(int i=0;i<m;i++)
           {
               if(ss-9>0)
               {
                   s[i]=9+'0';
                   ss=ss-9;
               }
               else
               {
                   s[i]=ss+'0';
                   break;
               }
           }
           for(int i=0;i<m;i++)
              printf("%c",s[i]);
           printf("
");
       }
    }
    return 0;
}

D题：

题意：给出一些有向边。然后问图中能够形成多少个菱形，。

思路：首先邻接边建图，然后直接枚举顶点。然后依据这些点进行扩展，在依据第二个点继续扩展，那么就得到了距离为2的点。左后就是求形成菱形的个数。那么就是C(1，X)*C（1。x-1）/2;最后累加就可以。。

题目：

D. Unbearable Controversy of Being

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Tomash keeps wandering off and getting lost while he is walking along the streets of Berland. It's no surprise! In his home town, for any pair of intersections there is exactly one way to walk from one intersection to the other one. The capital of Berland is very different!

Tomash has noticed that even simple cases of ambiguity confuse him. So, when he sees a group of four distinct intersections a, b, cand d, such that there are two paths from a to c — one through b and the other one through d, he calls the group a "damn rhombus". Note that pairs (a, b), (b, c), (a, d), (d, c) should be directly connected by the roads. Schematically, a damn rhombus is shown on the figure below:

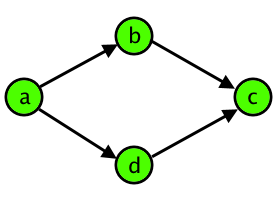
Other roads between any of the intersections don't make the rhombus any more appealing to Tomash, so the four intersections remain a "damn rhombus" for him.

Given that the capital of Berland has n intersections and m roads and all roads are unidirectional and are known in advance, find the number of "damn rhombi" in the city.

When rhombi are compared, the order of intersections b and d doesn't matter.

Input

The first line of the input contains a pair of integers n, m (1 ≤ n ≤ 3000, 0 ≤ m ≤ 30000) — the number of intersections and roads, respectively. Next m lines list the roads, one per line. Each of the roads is given by a pair of integers ai, bi (1 ≤ ai, bi ≤ n;ai ≠ bi) — the number of the intersection it goes out from and the number of the intersection it leads to. Between a pair of intersections there is at most one road in each of the two directions.

It is not guaranteed that you can get from any intersection to any other one.

Output

Print the required number of "damn rhombi".

Sample test(s)

input

5 4
1 2
2 3
1 4
4 3

output

1

input

4 12
1 2
1 3
1 4
2 1
2 3
2 4
3 1
3 2
3 4
4 1
4 2
4 3

output

12

代码：

#include<cstdio>
#include<cstring>

const int maxn=30000+10;
int head[maxn];

struct Edge
{
    int to,next;
}edge[maxn];

int n,m,edgenum[3000+10][3000+10],cnt;

void addegde(int x,int y)
{
    edge[++cnt].to=y;
    edge[cnt].next=head[x];
    head[x]=cnt;
}

int main()
{
   int l,r,ans;
   while(~scanf("%d%d",&n,&m))
   {
       cnt=0;
       memset(edgenum,0,sizeof(edgenum));
       memset(head,-1,sizeof(head));
       for(int i=1;i<=m;i++)
       {
           scanf("%d %d",&l,&r);
           addegde(l,r);
       }
       for(int i=1;i<=n;i++)
          for(int x=head[i];~x;x=edge[x].next)
       {
           int b=edge[x].to;
           for(int y=head[b];~y;y=edge[y].next)
           {
                int c=edge[y].to;
                if(i!=c)
                   edgenum[i][c]++;
           }
       }
       ans=0;
       for(int i=1;i<=n;i++)
          for(int j=1;j<=n;j++)
       {
           if(edgenum[i][j]>=2)
           {
               int xx=edgenum[i][j];
               ans+=(xx*(xx-1))/2;
           }
       }
       printf("%d
",ans);
   }
   return 0;
}