嗨，各位读者朋友们好久不见。在开始之前，再碎碎念几句。
笔者从2019年开始接触DSO，主要是得益于赵开勇博士的指导，将我领入DSO的大门。随后，在学习的过程中，也遇到非常多的挫折，虽然现在还有很多问题没彻底搞清楚，但是有幸的是，泡泡机器人SLAM的朋友们为我提供了非常多的帮助，其中包括但不限于勇哥（赵开勇）、威爷（曲星威）、晨博（邱笑晨）、金戈戈（涂金戈）、龚益群、吴佳田等大佬的指导和帮助。
虽然目前对于DSO认识还比较浅薄，但是也算是多少有些收获，因此想从现在开始把DSO整个体系再梳理一遍，更加系统地把各个模块的知识再学习学习，同时整理成笔记（博客），算是给自己定个小目标吧。毕竟，再不写博客的话，可能东西就快忘光了...
笔者想着跟往期的ORB-SLAM2一样，完成每一篇博客之后，再同步把对应的源码抠出来模块化，使其能够单独运行。不得不说，肢解一个SLAM系统，将其模块化，可真算是笔者特别喜欢的事情了... 虽然有可能会像往期的ORB-SLAM2一样，只实现一部分，但是笔者尽力而为吧。
接下来就是列一下表，将后续的博客内容都安排一下，笔者会主要围绕着这个大纲来写，至于啥时候能更完，这个事就随缘了。不过开弓没有回头箭，笔者就努力努力吧。
笔者能力有限，有写错的或者不足的地方，也烦请各位同行指正、交流。
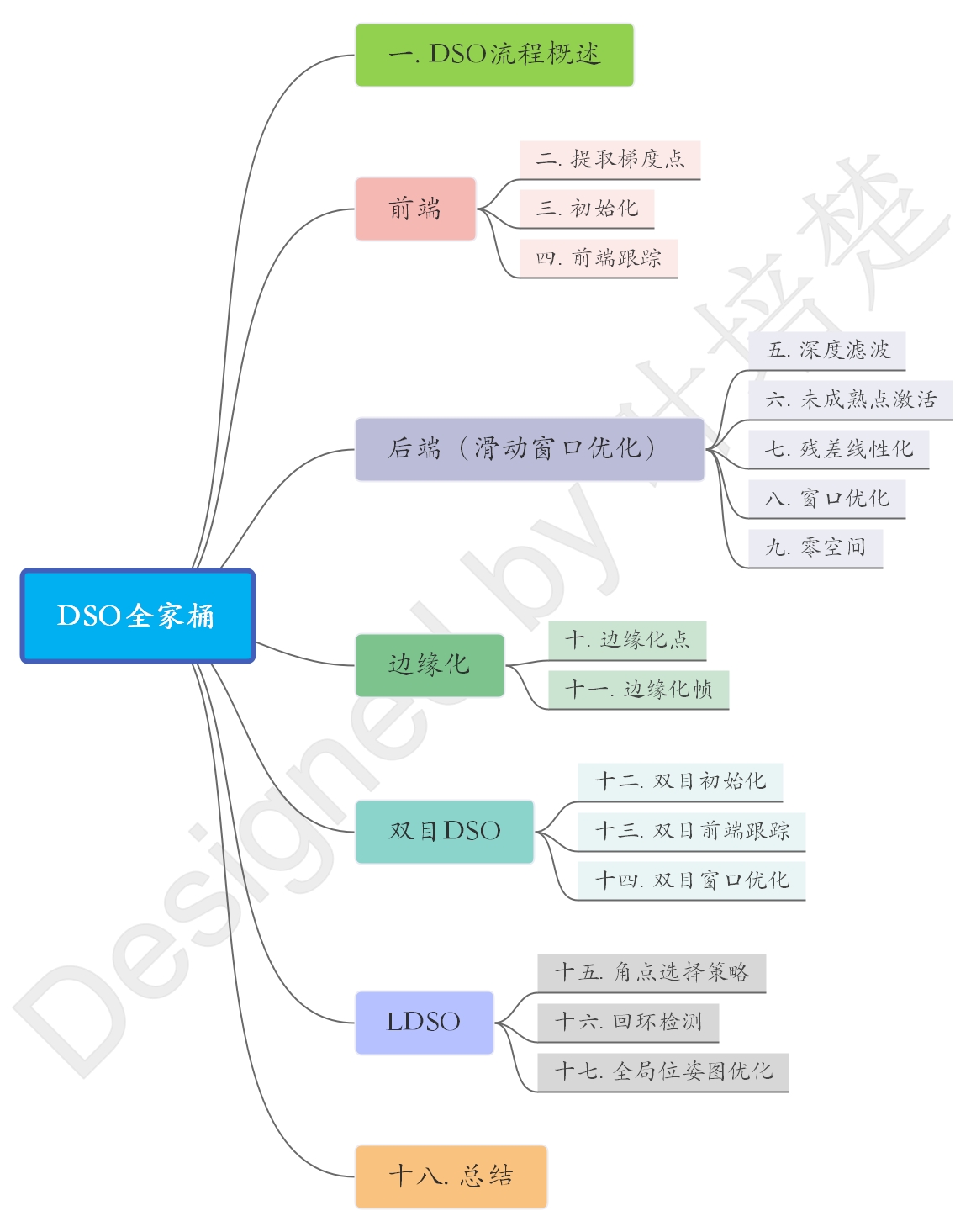图1. DSO全家桶博客标题列表
DSO流程概述
好的，那么我们就开始今天这一讲的内容了，先对DSO[1]的整体流程做一个概述。
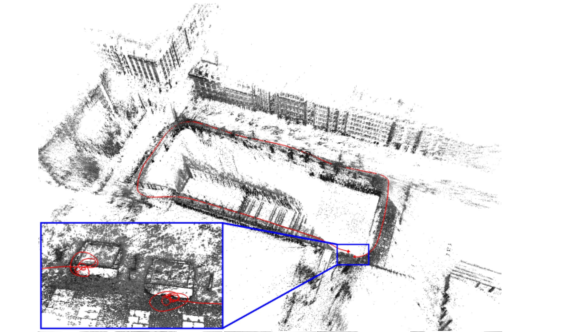
图2. DSO重建效果（参考DSO[1]）
DSO全称Direct Sparse Odometry，是慕尼黑工业大学计算机视觉实验室[2]的雅各布博士在2016年发表的工作。在DSO之前，雅各布博士的另一个直接法巨作是LSD-SLAM[3]及其双目版本LSD-SLAM2[4]。非常幸运的是，高翔博士在知乎上的文章DSO详解[5]对DSO做了非常详细的分析，因此我们可以非常系统的了解DSO系统的整体框架。
为了更加流畅地对整个系统流程进行介绍，笔者参考了涂金戈的博客DSO代码框架。
一. 前端
前端的主要任务是对传感器的输入进行预处理，随后进行数据关联，并构建目标函数，通过优化目标函数估计初始的相机位姿变换。
1. 初始化
初始化阶段需要两帧图像：
第一帧是作为基准帧，即DSO视第一帧所在的相机坐标系为世界坐标系。对图像构建图像金字塔，逐层对图像提取梯度较大的点，并在层间设置关联关系，同时为每个点初始化一个深度值，通常为1。
第二帧基于第一帧的点，构建光度误差函数，通过Gauss-Newton法优化得到初始相对位姿。随后将第一帧设置为关键帧，将第一帧中提取的梯度点激活，将其加入滑动窗口的优化中。在DSO中，点分为两种类型，一种是激活点、一种是未成熟点。通常在图像中刚刚提取的或者深度未收敛的点称为未成熟点，具有非常大的深度范围。通过深度滤波器在帧间不断地滤波，使得点的深度不断收敛，最终得到的点会被激活，加入滑动窗口中，这种点被称为激活点。
DSO中的点在刚刚提取时，都是设置为深度范围非常大的未成熟点。而在前端跟踪阶段，新帧都是不会先提取点的，只有在确定为关键帧时，经过窗口优化后，才会对当前帧提取点，并将滑动窗口所有激活点投影到该帧中构建深度图，作为后续帧的参考帧。而第二帧就是这种情况，在初始化后，进入滑动窗口优化，在这个阶段会判断初始化是否成功，若残差太大，则判定初始化失败，需要重新设置第一帧，重复上述过程。
2. 跟踪
从第三帧开始，进入正式的跟踪流程。需要明确的一点是，直接法不同于特征点法，特征点法可以通过特征提取以及特征匹配进行帧间数据关联，并采用多视图几何的方式构建帧间约束关系，比如采用RANSAC PNP或者对极几何等方式估算初始位姿变换。而直接法没有这种数据关联方式，它必须通过帧间运动将参考帧中的点反投影到当前帧中构建光度误差函数，从而优化帧间相对位姿。那么问题来了，又要用相对位姿来做反投影、又要反过来用这个投影的结果构建的误差函数优化这个相对位姿，那么这个初始的位姿怎么来呢？直接法中采用的方式是运动模型，通过考虑1倍的、2倍的、0.5倍的、0倍的速度假设，构建多个运动模型，而基数是基于前几帧间的相对位姿变换。
在得到了运动模型之后，便是逐个对运动模型进行验证。即采用运动模型，将参考帧中的点反投影到当前帧中构建光度误差函数，利用Gauss-Newton法优化目标函数，若结果收敛，则跳出模型验证，直接给出相对位姿初值。否则，重复上述过程。
二. 后端
后端的内容主要包括深度滤波、未成熟点激活、窗口优化。
1. 深度滤波
如前所述，所有未成熟点的深度范围值都是非常大，在DSO中初始化为[0, +∞]。通过在帧间进行极线搜索，找到匹配的点后，采用Gauss-Newton进一步优化，值得注意的是，每次深度滤波器滤波后得到的结果仍然是一个深度范围，而不是单一一个深度值。深度滤波在关键帧和非关键帧中都会用到。后续的博文中我们会详细介绍。
2. 未成熟点激活
通过多次深度滤波，有些关键帧的未成熟点的深度范围已经收敛，通过多种条件判定后，将未成熟点激活，加入滑动窗口中进行联合优化。
3. 窗口优化
通过将滑动窗口中的所有关键帧位姿和激活点全部联合起来优化一个总的光度误差函数，相比于两帧之间的约束，滑动窗口中提供的约束条件更多，可以优化前端估计的相对位姿初值。后续我们会详细介绍。
三. 边缘化
在滑动窗口的优化中，随着新的关键帧和点的加入，滑动窗口的大小会不断增大，最终失去它灵活高效的功能。为了保持固定大小的窗口（DSO默认值是7个关键帧和2000个激活点），DSO采用边缘化策略将旧帧和旧点剔除。如图3左图所示，优化问题中的海塞矩阵具有良好的稀疏性，这种稀疏性可以使得SLAM问题的求解更加高效。但是，有些错误的操作通常会导致海塞矩阵的稀疏结构被破坏。参考所长（贺一家）的博文：SLAM中的marginalization 和 Schur complement，由于同一个点，可以被不同的关键帧观测到，会产生约束关系。若我们贸然地将某个状态给边缘化了，会得到图3右图所示的结果，即稀疏性被完全破坏了。而在DSO中，对于被多个关键帧观测到的点，若已经到了需要边缘化的阶段，通常会选择直接舍弃。并且，DSO采用先边缘化点，再边缘化关键帧的目的也是为了保证海塞矩阵的稀疏性。
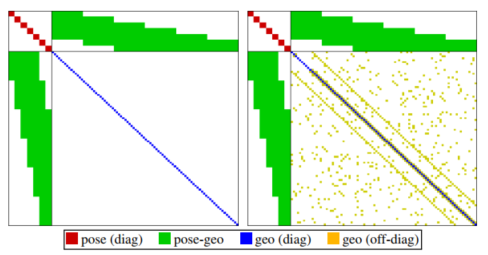
图3. 海塞矩阵的稀疏性（参考DSO[1]）
四. 参考文献
[1] Engel J, Koltun V, Cremers D. Direct sparse odometry[J]. IEEE transactions on pattern analysis and machine intelligence, 2017, 40(3): 611-625.
[2] 慕尼黑工业大学计算机视觉实验室
[3] Engel J, Schöps T, Cremers D. LSD-SLAM: Large-scale direct monocular SLAM[C]//European conference on computer vision. Springer, Cham, 2014: 834-849.
[4] Engel J, Stückler J, Cremers D. Large-scale direct SLAM with stereo cameras[C]//2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2015: 1935-1942.
[5] DSO详解
[6] DSO代码框架
[7] Mur-Artal R, Tardós J D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras[J]. IEEE Transactions on Robotics, 2017, 33(5): 1255-1262.
[8] 深度滤波器
[9] SLAM中的marginalization 和 Schur complement
最后打个广告，欢迎关注泡泡机器人SLAM微信公众号，更欢迎加入泡泡大家庭。