排序

排序

排序分类

常见排序可以分为两大类：

比较排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。

非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

算法复杂度

排序方法	时间复杂度（平均）	时间复杂度（最坏）	时间复杂度（最好）	空间复杂度	稳定性
插入排序	O(n2)	O(n2)	O(n)	O(1)	稳定
希尔排序	O(n1.3)	O(n2)	O(n)	O(1)	不稳定
选择排序	O(n2)	O(n2)	O(n2)	O(1)	不稳定
堆排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(1)	不稳定
冒泡排序	O(2)	O(2)	O(2)	O(1)	稳定
快速排序	O(nlog2n)	O(n2)	O(nlog2n)	O(nlog2n)	不稳定
归并排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(n)	稳定
计数排序	O(n+k)	O(n+k)	O(n+k)	O(n+k)	稳定
桶排序	O(n+k)	O(n2)	O(n2)	O(n+k)	稳定
基数排序	O(n*k)	O(n*k)	O(n*k)	O(n+k)	稳定

相关概念

稳定排序：如果a与b相等，且排序前在a在b的前面，排序后a仍然在b的前面，则是稳定排序。

不稳定排序：如果a与b相等，且排序前在a在b的前面，排序后a却在b的后面，则是不稳定排序。

1.冒泡排序

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误，就把它们交换过来。重复地进行比较交换，直到没有再需要交换的数，这时该数列就已经排序完成。

1.1算法描述

1）比较相邻的元素。如果前一个比后一个大，则交换他们值。

2）对每一个相邻的未排序的元素做以上的比较操作，这样每次都可以把最大值存到未排序区域的结尾位置。

3）针对所有的元素重复以上步骤，一共n - 1轮，最后一个元素不用排序。

1.2动图演示

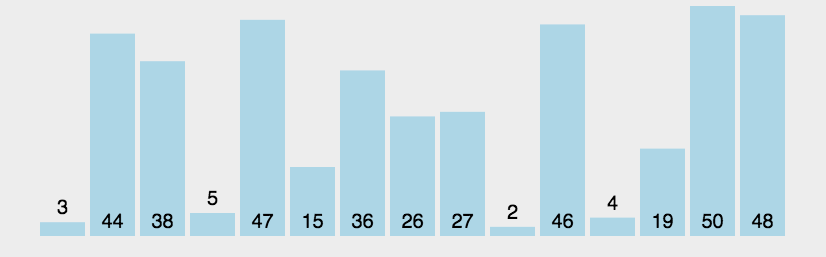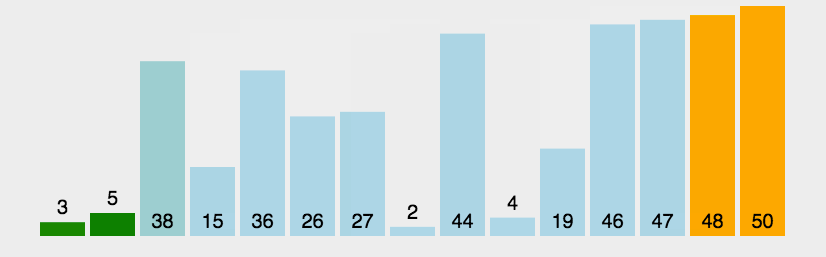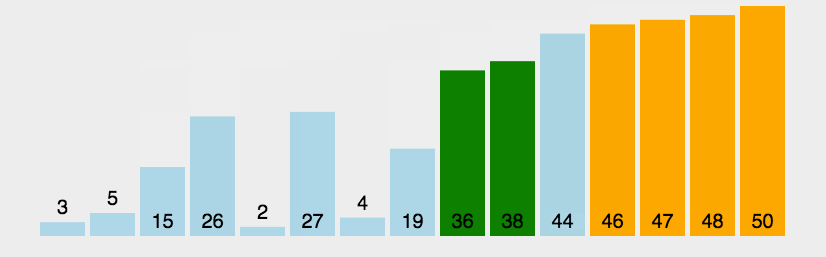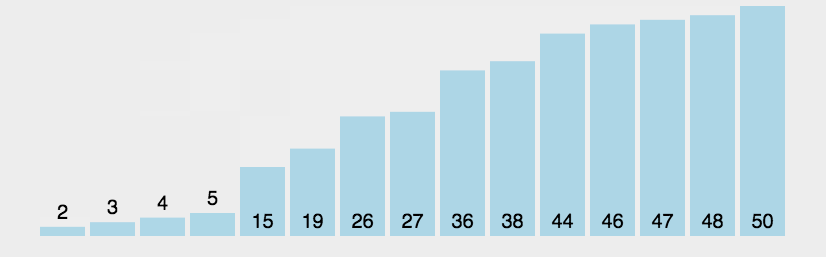
1.3 代码

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <time.h>

#define swap(a, b) ({
    __typeof(a) tmp = a;
    a = b, b = tmp;
})

int arr[10];

void rant_arr(void) {
    srand(time(0));
    for (int i = 0; i < 10; i++) {
        arr[i] = rand() % 100;
    }
}

void print_arr(void) {
    for (int i = 0; i < 10; i++) {
        printf("%d ", arr[i]);
    }
    printf("
");
}

void bubble_sort(int *arr, int n) {
    int flag = 1;
    for (int i = 0; i < n - 1 && flag == 1; i++) {
        flag = 0;
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] < arr[j + 1]) continue;
            swap(arr[j], arr[j + 1]);
            flag = 1;
        }
    }
}

int main(int argc, char *argv[]) {
    rant_arr();
    printf("before bubble sort:
");
    print_arr();
    bubble_sort(arr, 10);
    printf("after bubble sort:
");
    print_arr();
}

2.选择排序

选择排序（select sort）是一种最简单直观的排序算法。原理：首先在排序序列中找到最小（最大）元素，然后存放到排序序列的起始位置，最后再继续从剩余的未排序元素中继续寻找最值直到整个数列存放完毕。

2.1算法描述

1）取序号为第i[1...n-1]元素，并假设其为最小（大）值；

2）把最值与剩余范围[i+1...n-1]的所有值进行对比比较，如果有存在比序号i对应的元素小（大）的元素，则更新最值序号；

3）重复以上步骤n-1次，则排序完毕。

2.2动图演示

2.3代码

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <time.h>

#define swap(a, b) ({
    __typeof(a) tmp = a;
    a = b, b = tmp;
})

int arr[10];

void rant_arr(void) {
    srand(time(0));
    for (int i = 0; i < 10; i++) {
        arr[i] = rand() % 100;
    }
}

void print_arr(void) {
    for (int i = 0; i < 10; i++) {
        printf("%d ", arr[i]);
    }
    printf("
");
}

void select_sort(int *arr, int n) {
    for (int i = 0; i < n - 1; i++) {
        int min = i;
        for (int j = i + 1; j < n; j++ ) {
            if (arr[min] < arr[j]) continue;
            min = j;
        }
        if (min != i) {
            swap(arr[min], arr[i]);
        }
    }
}

int main(int argc, char *argv[]) {
    rant_arr();
    printf("before select sort:
");
    print_arr();
    select_sort(arr, 10);
    printf("after select sort:
");
    print_arr();
}

3.插入排序

插入排序（insert sort）也是一种简单直观的排序算法。将整个序列分为有序部分和无序部分，并从无序部分开始取数，从有序序列中从后先前比较，在有序序列中找到相应的位置插入。

3.1算法描述

1）去第一个元素作为有序序列的起始元素；

2）从下一个元素开始取数，并用这个元素在有序序列中从后往前比较；

3）若该元素比当前比较的有序元素小（大），则交换位置，且用这个元素继续在有序序列中往前比较；否则，则重复第2步骤，重新在无序序列中取出元素；

4）重复以上步骤n-1轮，则排序完毕。

3.2 动图演示

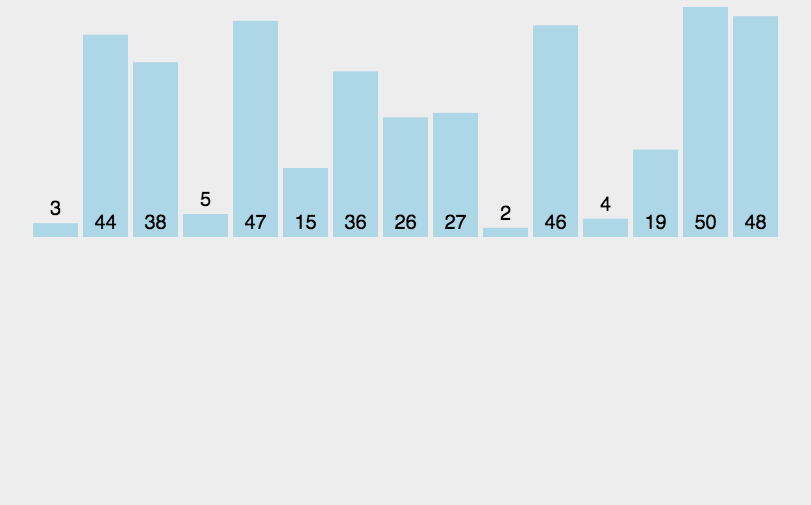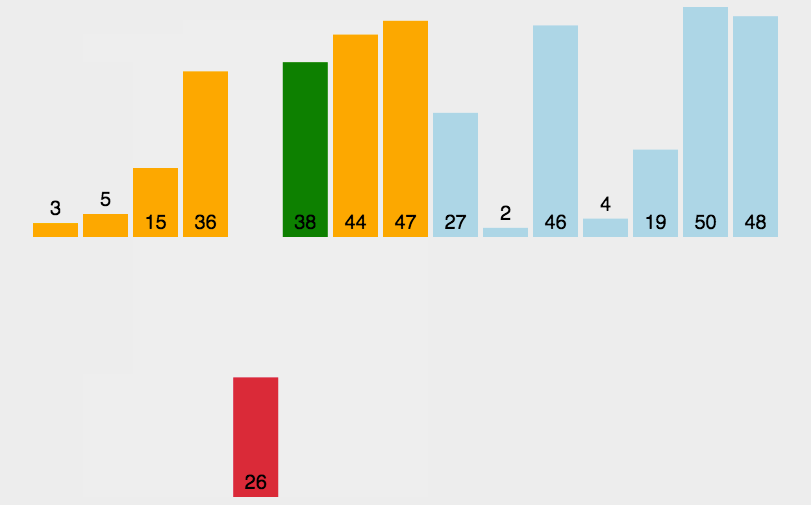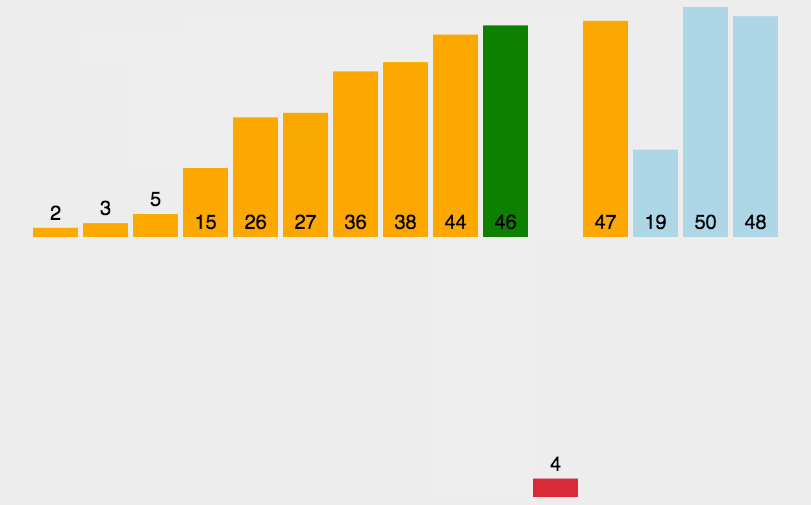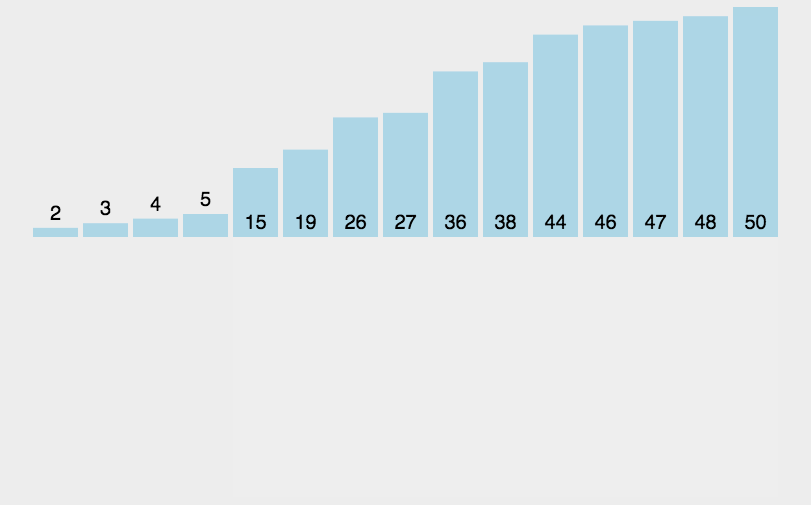
3.3 代码

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <time.h>

#define swap(a, b) ({
    __typeof(a) tmp = a;
    a = b, b = tmp;
})

int arr[10];

void rant_arr(void) {
    srand(time(0));
    for (int i = 0; i < 10; i++) {
        arr[i] = rand() % 100;
    }
}

void print_arr(void) {
    for (int i = 0; i < 10; i++) {
        printf("%d ", arr[i]);
    }
    printf("
");
}


void insert_sort(int *arr, int n) {
    for (int i = 1; i < n; i++) {
        for (int j = i; j > 0; j--) {
            if (arr[j] > arr[j - 1]) {
                break;
            }
            swap(arr[j], arr[j - 1]);
        }
    }
}

int main(int argc, char *argv[]) {
    rant_arr();
    printf("before insert sort:
");
    print_arr();
    insert_sort(arr, 10);
    printf("after insert sort:
");
    print_arr();
}

4.归并排序

归并排序（merge sort）采用归并的思想进行排序，该算法通过利用经典的分治策略来实现排序。

4.1 算法描述

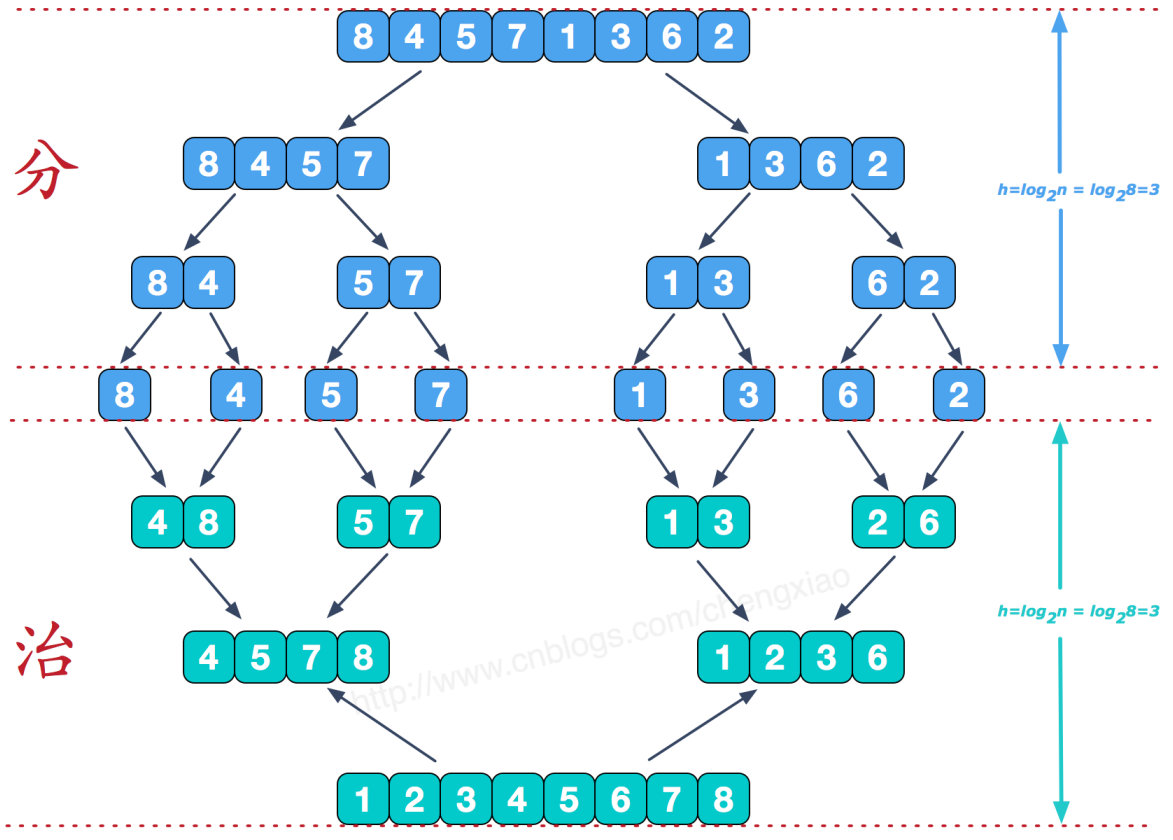
分过程
1）将整个序列一分为二；

2）得到的子序列继续递归一分为二；

3）重复步骤2，直至分出来的子序列的元素数量小于等于两个时，停止分割；

4）根据子序列的元素数量进行相应操作：
若子序列数量为2，则进行比较，值小（大）存放在前面；
若子序列数量为1，则不做任何操作；
治过程
1）申请一个相邻的两个子序列大小之和的空间；

2）依次从相邻的两个序列中取出一个元素进行对比，小（大）的存到新申请的空间中，当比较完两个子序列后，回溯；

3）重复1和2操作，直至回溯到开始的完整序列。

图片演示

代码

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <string.h>
#include <time.h>

#define swap(a, b) ({
    __typeof(a) tmp = a;
    a = b, b = tmp;
})

int arr[10];

void rant_arr(void) {
    srand(time(0));
    for (int i = 0; i < 10; i++) {
        arr[i] = rand() % 100;
    }
}

void print_arr(void) {
    for (int i = 0; i < 10; i++) {
        printf("%d ", arr[i]);
    }
    printf("
");
}

void merge_sort(int *arr, int l, int r) {
    if (r - l <= 1) {
        if (r - l == 1 && arr[l] > arr[r]) {
            swap(arr[l], arr[r]);
        }
        return ;
    }
    int mid = (l + r) / 2;
    merge_sort(arr, l, mid);
    merge_sort(arr, mid + 1, r);
    int *temp = (int *)malloc(sizeof(int) * (r - l + 1));
    int p1 = l, p2 = mid + 1, k = 0;
    while (p1 <= mid || p2 <= r) {
        if (p2 > r || (p1 <= mid && arr[p1] < arr[p2])) {
            temp[k++] = arr[p1++];
        } else {
            temp[k++] = arr[p2++];
        }
    }
    memcpy(arr + l, temp, sizeof(int) * (r - l + 1));
    free(temp);
    return ;
}

int main(int argc, char *argv[]) {
    rant_arr();
    printf("before merge sort:
");
    print_arr();
    merge_sort(arr, 0, 9);
    printf("after merge sort:
");
    print_arr();
}

5快速排序

快速排序（merge sort）跟归并排序一样，也是通过利用经典的分治策略来实现排序。

5.1 算法描述

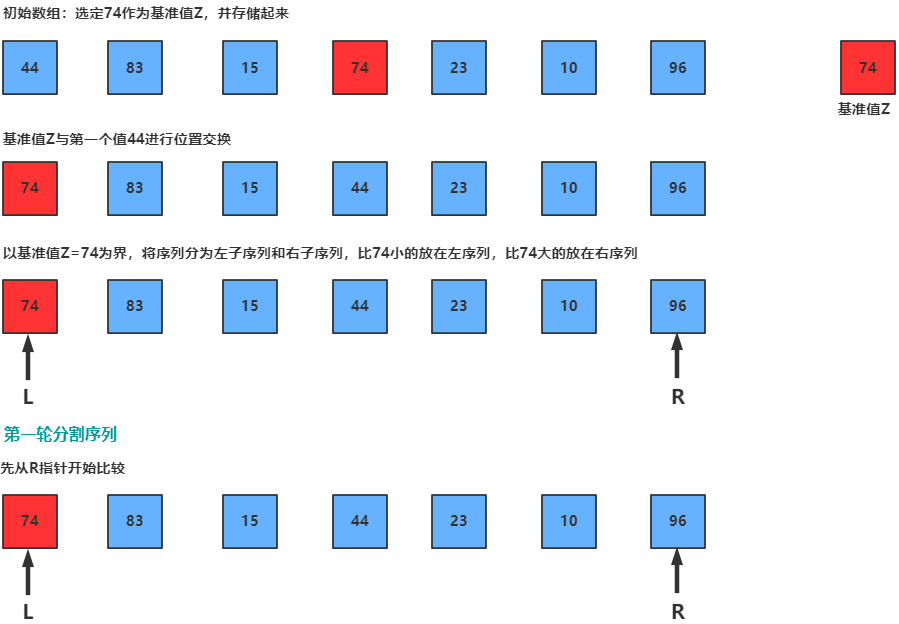
1．先从数列中取出一个数作为基准数。
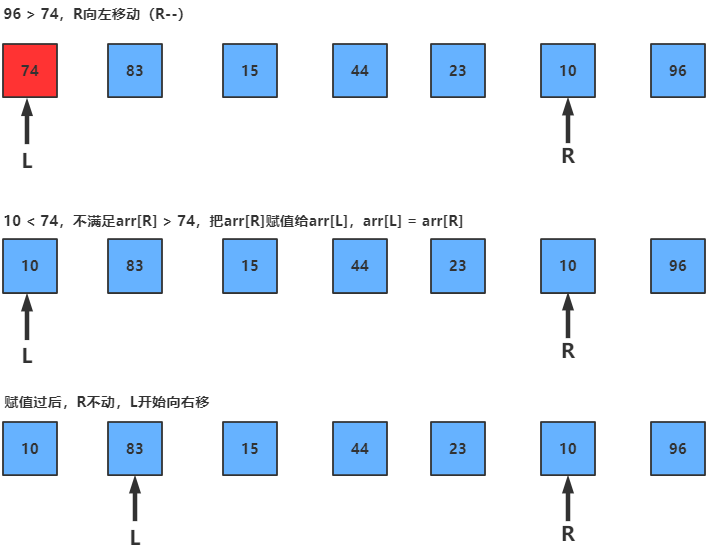
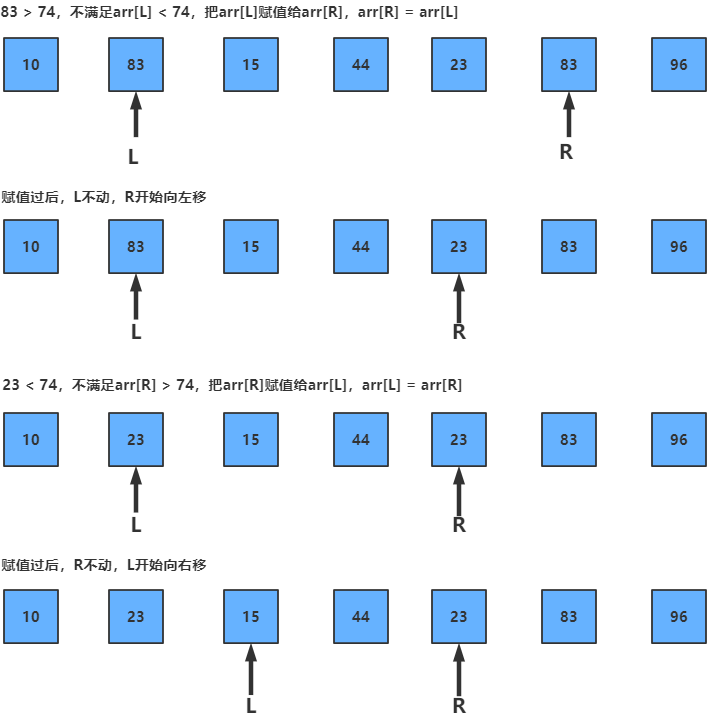
2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
3．再对左右区间重复第二步，直到各区间只有一个数。
对于基准值的取法，一般有三种
1.待排序列中的第一个元素；
2.待排序列中的中间元素；
3.随机选取待排序列中的元素。
这里，我们采用方法2来取基准值，这样可以防止快速排序退化。。

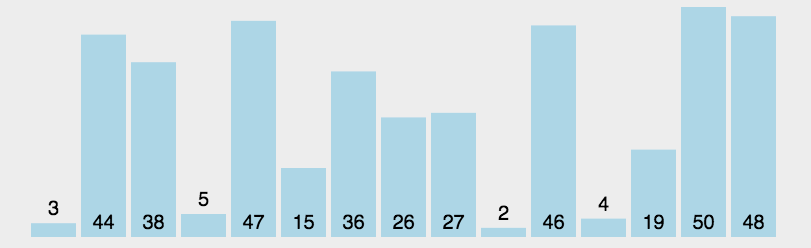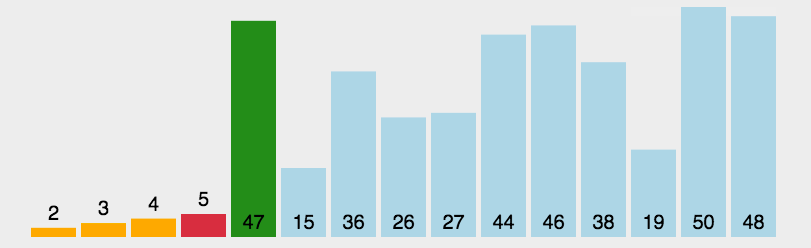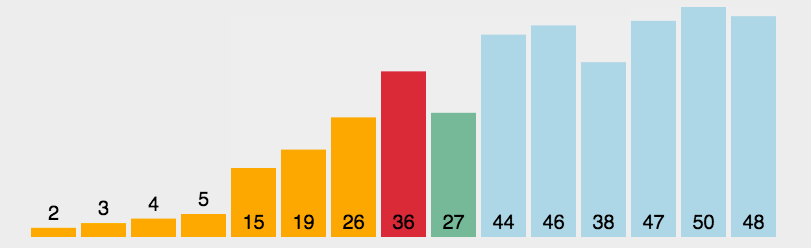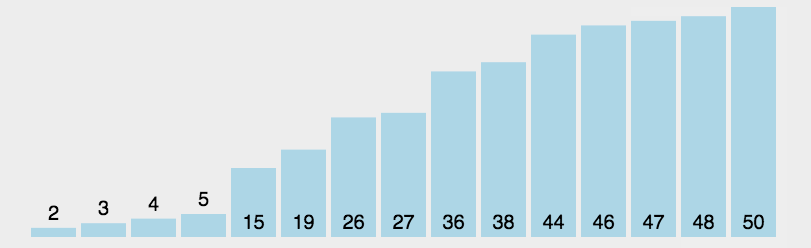
5.2 图片演示

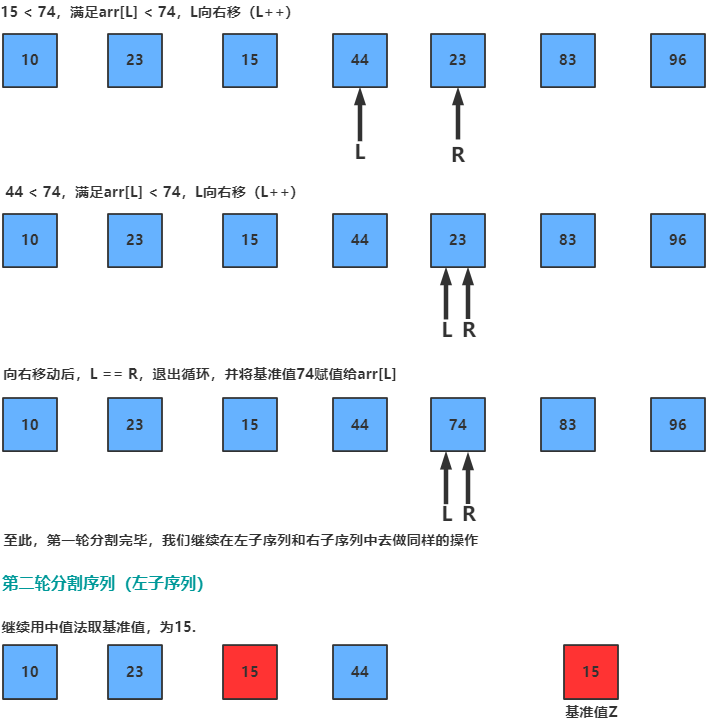
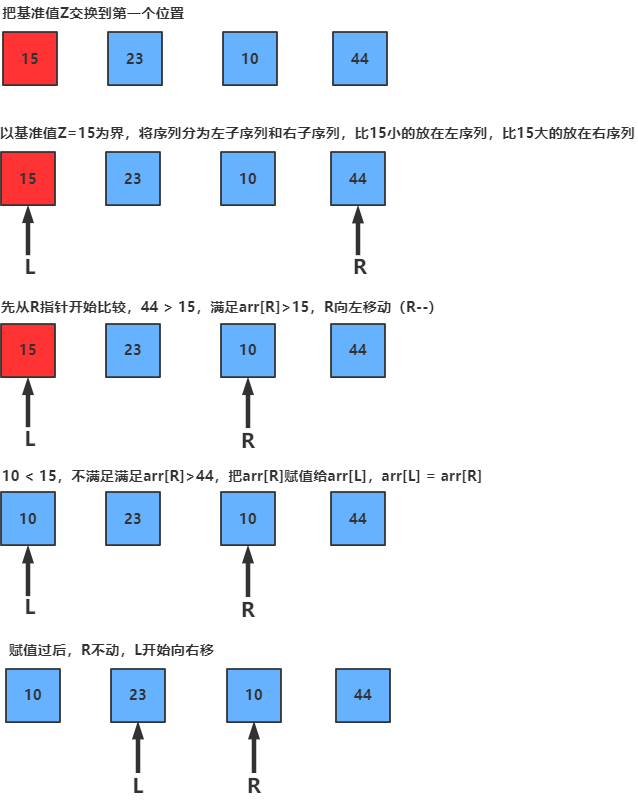
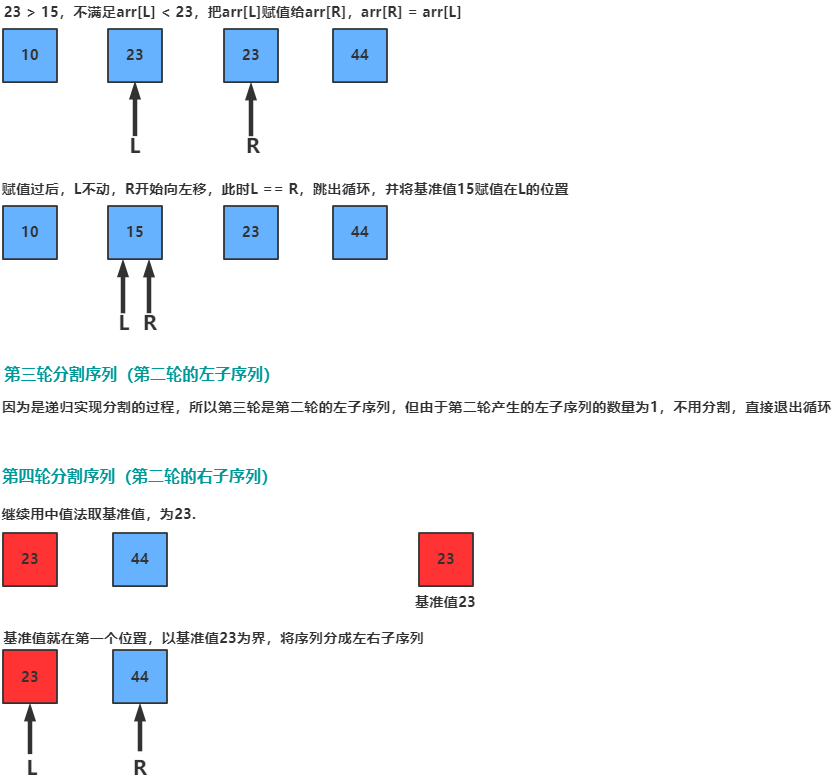
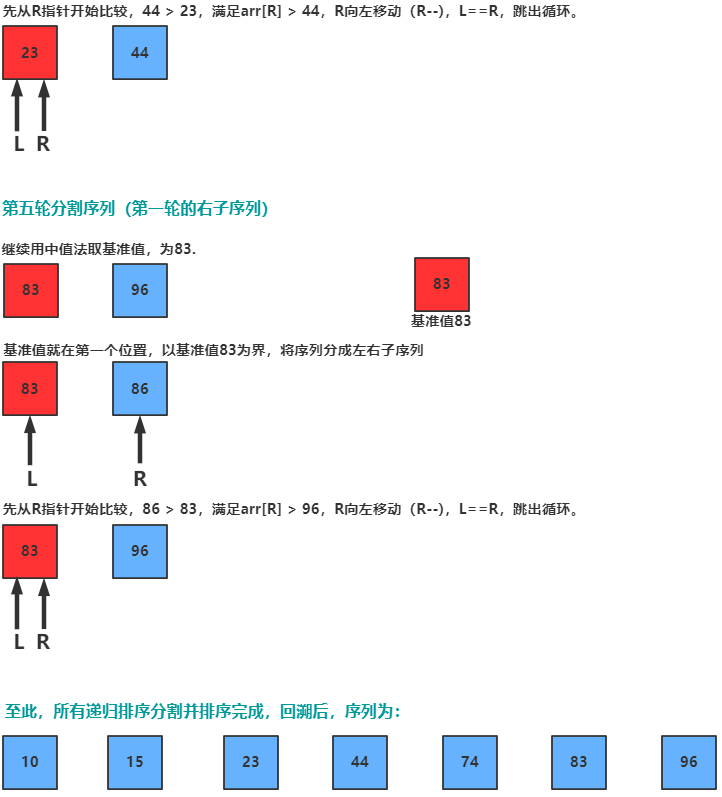
5.3 代码

/*************************************************************************
        > File Name: quick_sort.c
        > Author: ydqun
        > Mail: qq28*****5@163.com
        > Created Time: Thu 06 May 2021 11:13:51 AM CST
 ************************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <time.h>

#define swap(a, b) ({
    __typeof(a) tmp = a;
    a = b, b = tmp;
})

int arr[10];

void rant_arr(void) {
    srand(time(0));
    for (int i = 0; i < 10; i++) {
        arr[i] = rand() % 100;
    }
}

void print_arr(void) {
    for (int i = 0; i < 10; i++) {
        printf("%d ", arr[i]);
    }
    printf("
");
}

void quick_sort(int *num, int l, int r) {
    if (l >= r) {
        return ;
    }
    int x = l, y = r, z = num[(x + y) >> 1];
    swap(arr[x], z);
    while (x != y) {
        while (x < y && num[y] > z) {
            y--;
        }
        if (x < y) {
            num[x++] = num[y];
        }
        while (x < y && num[x] < z) {
            x++;
        }
        if (x < y) {
            num[y--] = num[x];
        }
    }
    num[x] = z;
    quick_sort(num, l, x - 1);
    quick_sort(num, x + 1, r);
}

int main(int argc, char *argv[]) {
    rant_arr();
    printf("before quick sort:
");
    print_arr();
    quick_sort(arr, 0, 9);
    printf("after quick sort:
");
    print_arr();
}

6 堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。建议先去理解堆结构再来理解堆排序，不清楚堆结构的可以打开此链接https://www.cnblogs.com/ydqblogs/p/14764781.html。

6.1 思想

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

6.2 图示

假设有下图的一个数组

数组的下标0不存储元素，而是从下标1开始存储（这里这样做的目的为了便于完全二叉树节点序号的计算）。
我们根据数组元素的下标，把所有元素构造成一个二叉树， 如下图。

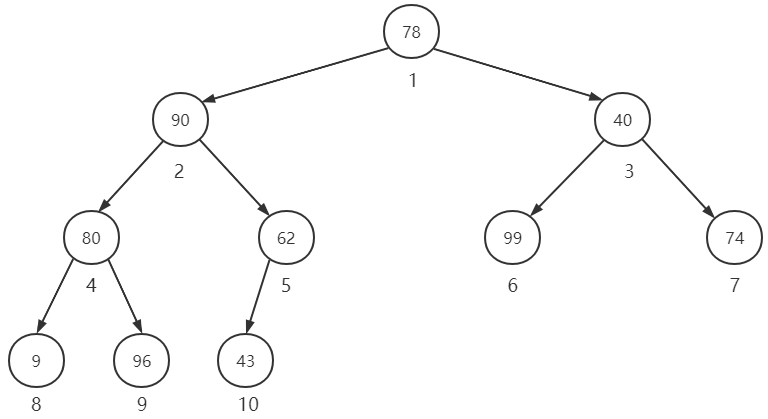
由上图看出，这个二叉树是完全二叉树，而二叉树有如下性质：
性质：若对一棵有n个节点的完全二叉树进行顺序编号(1 <= i <= n)，那么，对于编号i（i >= 1）的节点：
1）当i = 1时，该节点为根节点，且它没有父节点；
2）当i > 1时，该节点的双清节点为i/2；
3）若2i <= n，则有存在编号为2i的左孩子节点，否则则没有左孩子节点；
4）若2i + 1 <= n，则存在编号为2i + 1的右孩子节点，否则则没有右孩子节点。
我们可以根据这个性质把这棵二叉树调整为一个大顶堆，至于调整的策略，我们采取从序号为n/2的节点开始到序号为1结束，自上向下对比调整，详细过程看下图比较容易理解。
从n/2 = 5处开始调整

在n/2 - 1 = 4号节点继续调整

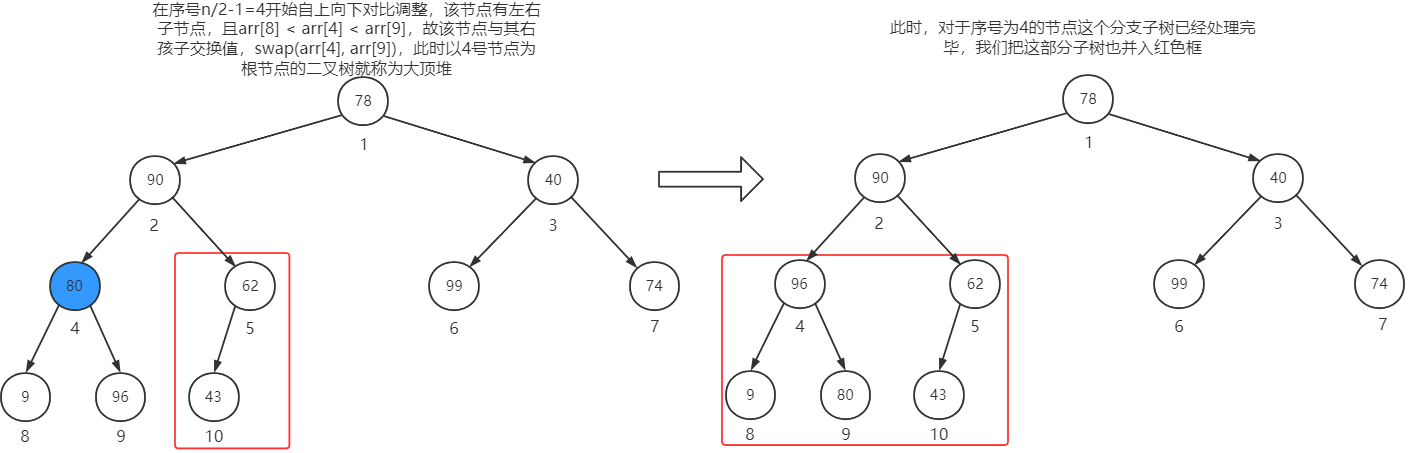
在n/2 - 2 = 3号节点继续调整

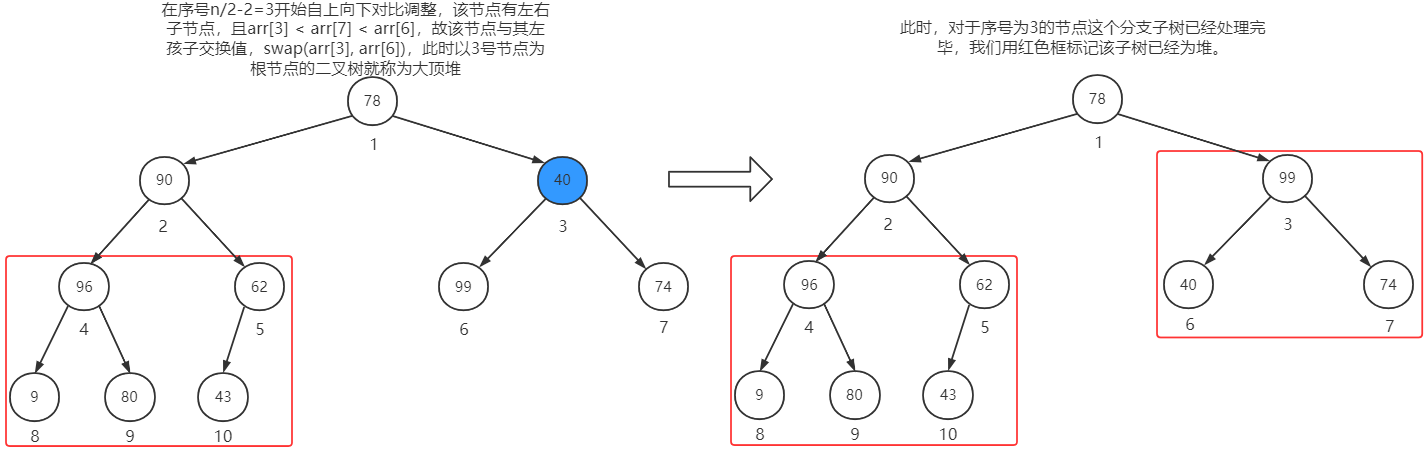
在n/2 - 3 = 2号节点继续调整

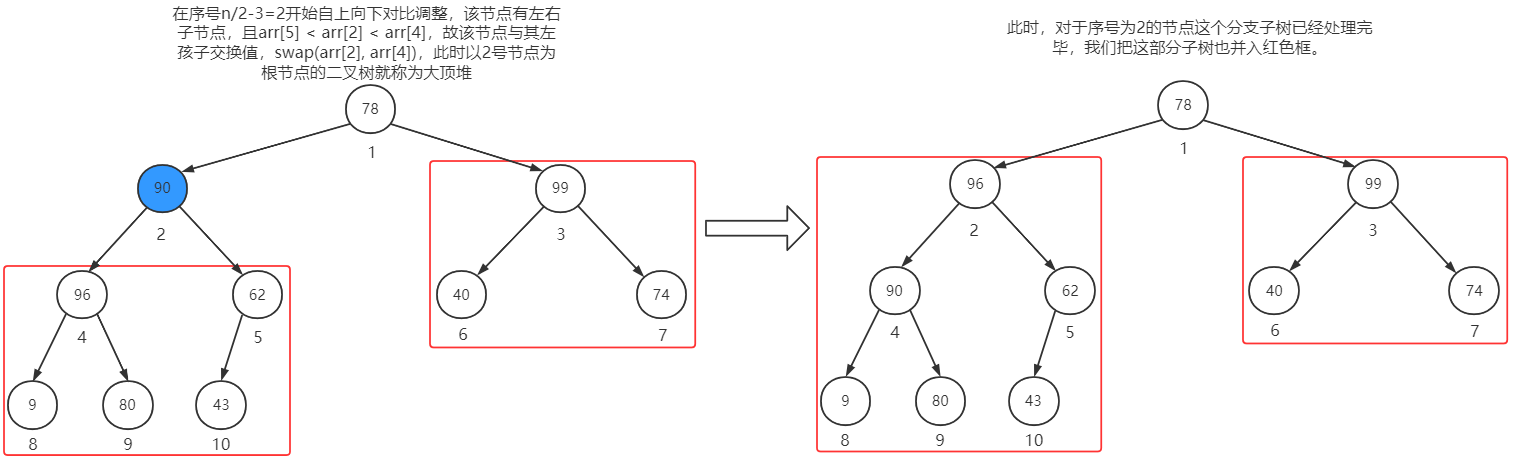
在n/2 - 4 = 1号节点继续调整

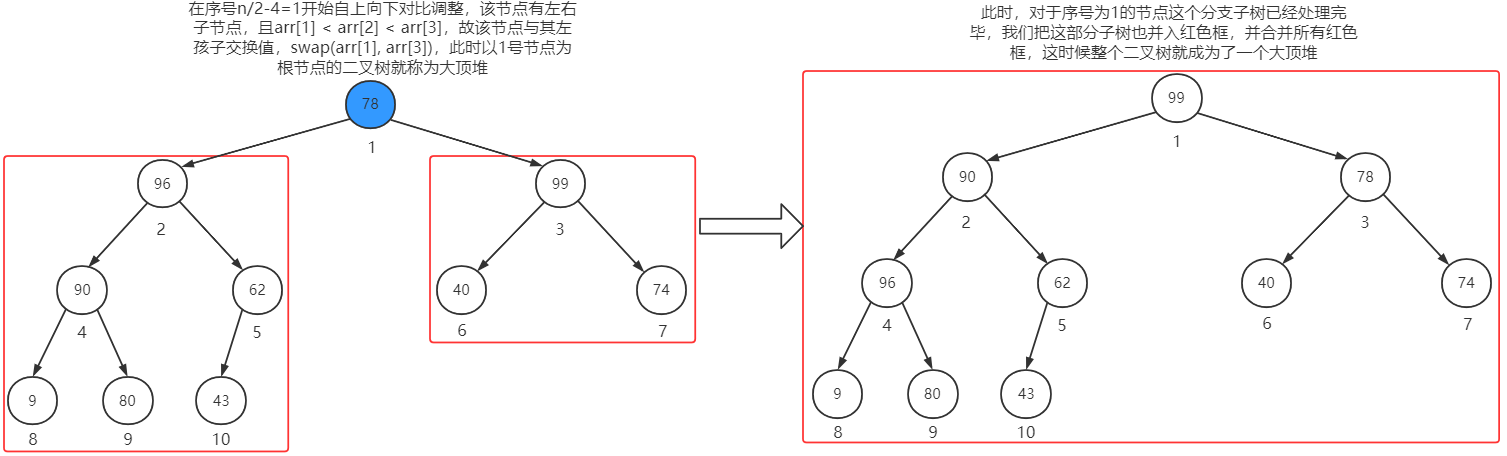
此时，我们完成了堆排序的最重要的一步，把无序数组调整成一个大顶堆，接着我们需要做的是：将堆顶元素与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n-1个元素的次小值。如此反复执行，便能得到一个有序序列了.
堆顶元素与第10个元素交换位置，再调整成堆

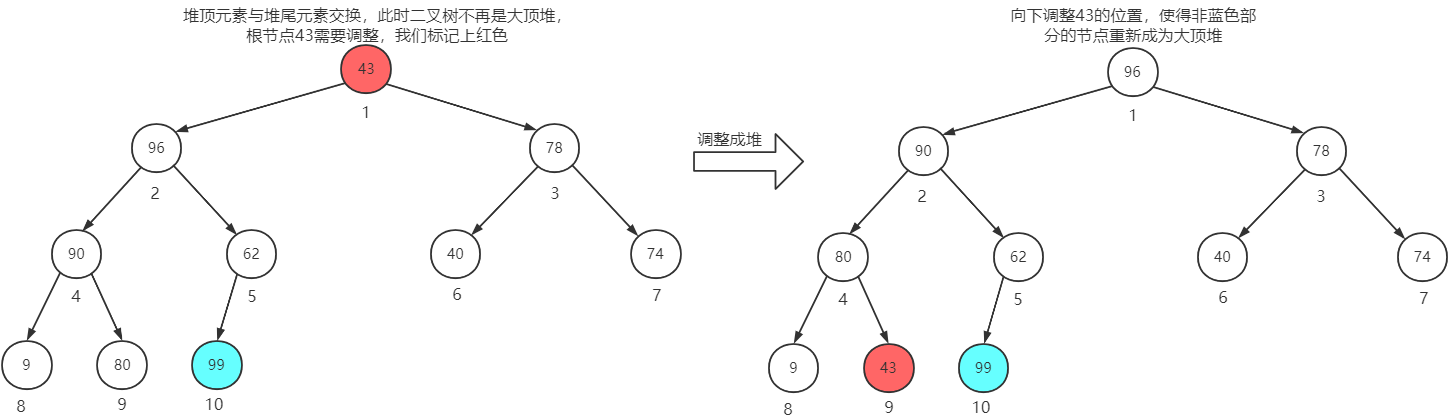
堆顶元素与第9个元素交换位置，再调整成堆

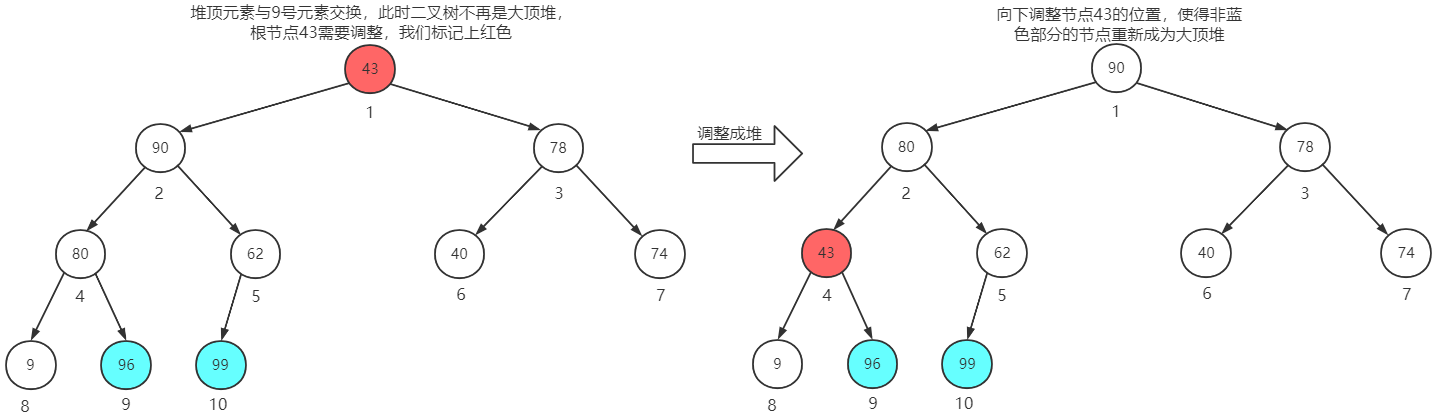
堆顶元素与第8个元素交换位置，再调整成堆

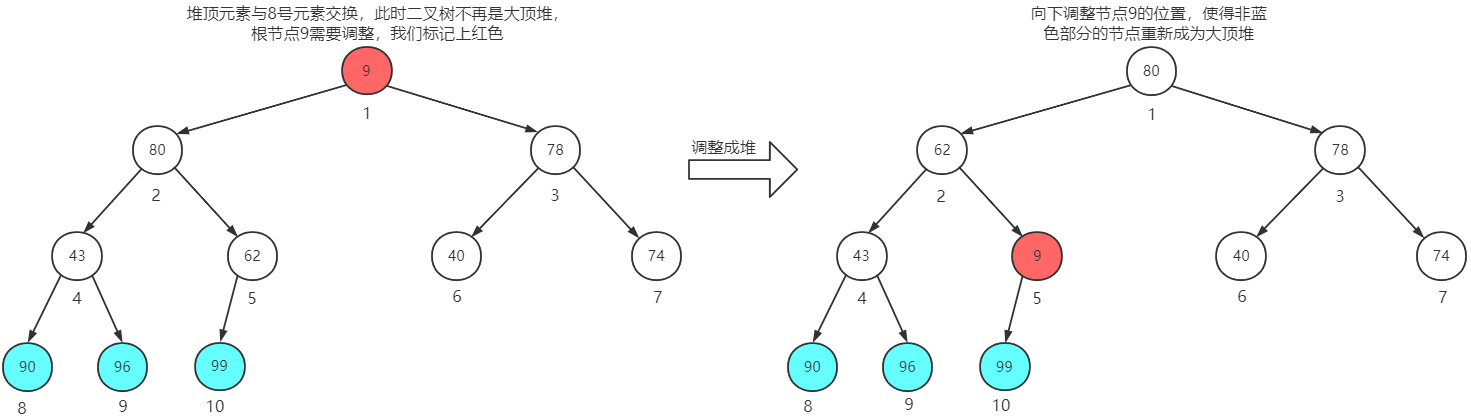
堆顶元素与第7个元素交换位置，再调整成堆

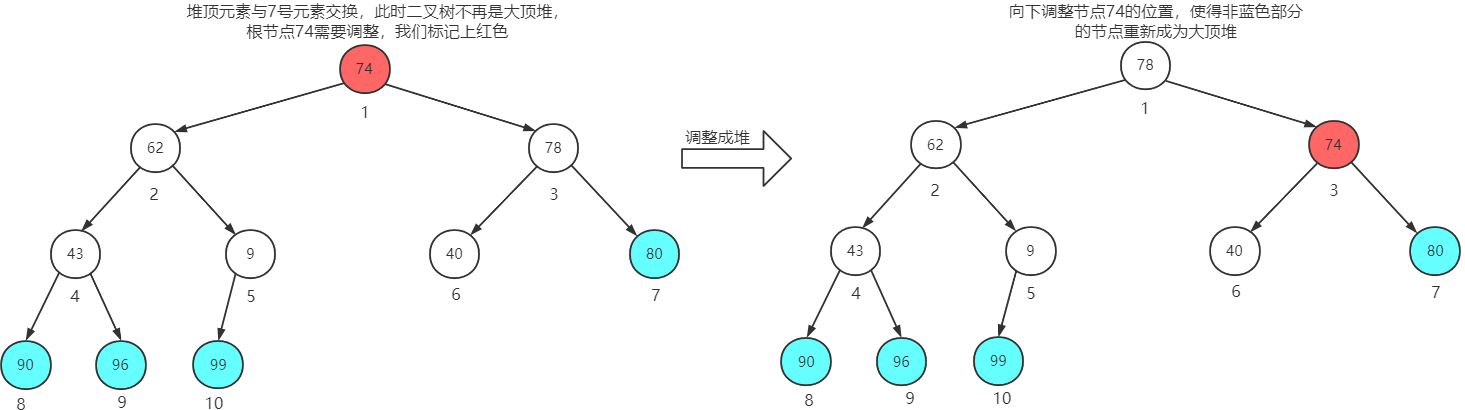
堆顶元素与第6个元素交换位置，再调整成堆

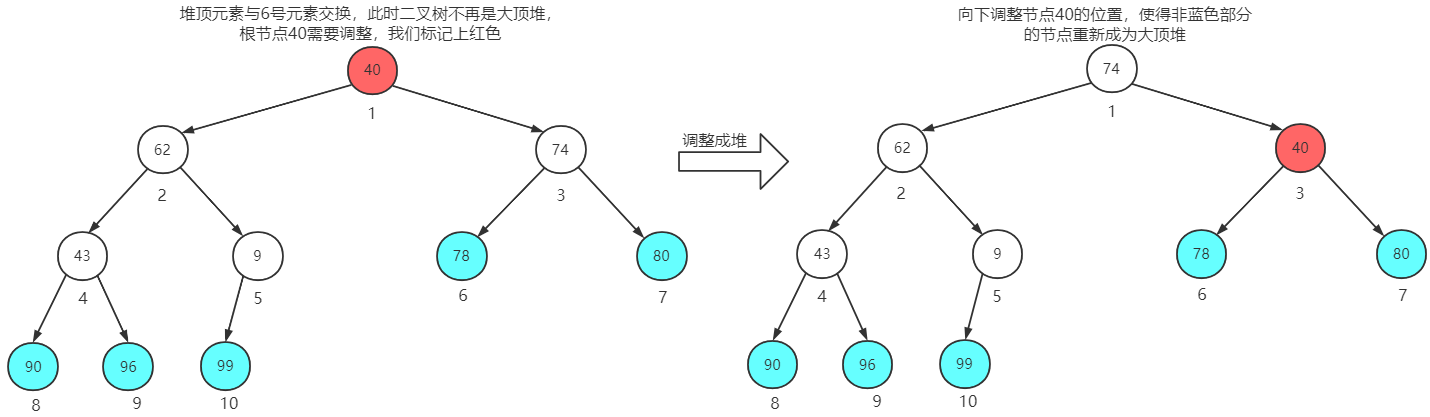
堆顶元素与第5个元素交换位置，再调整成堆

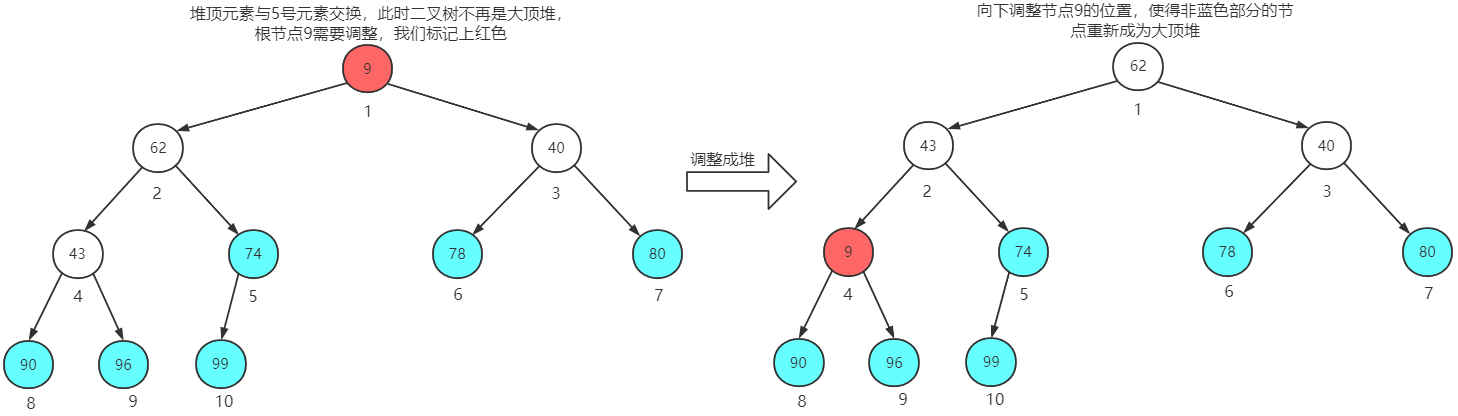
堆顶元素与第4个元素交换位置，再调整成堆

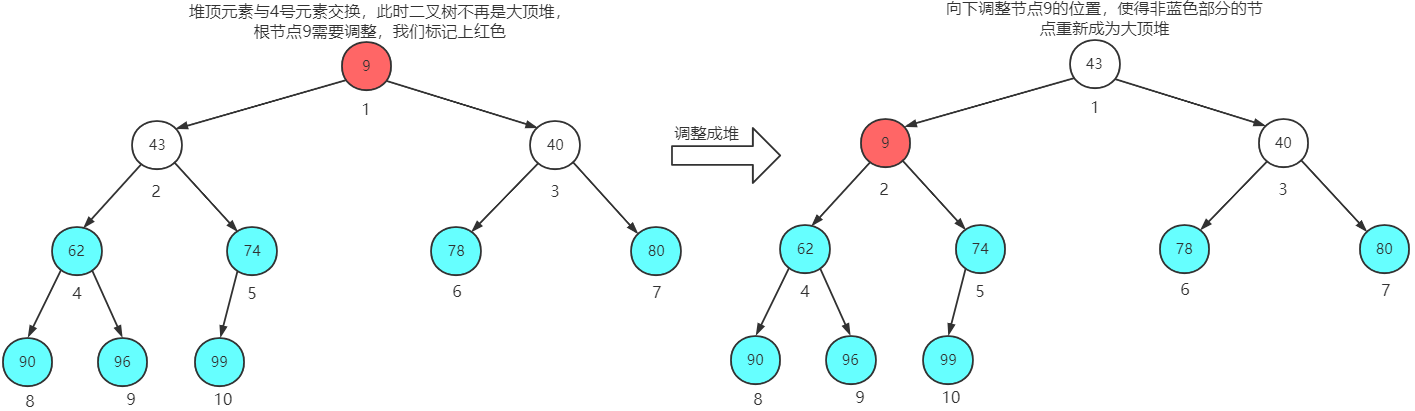
堆顶元素与第3个元素交换位置，无需再调整成堆

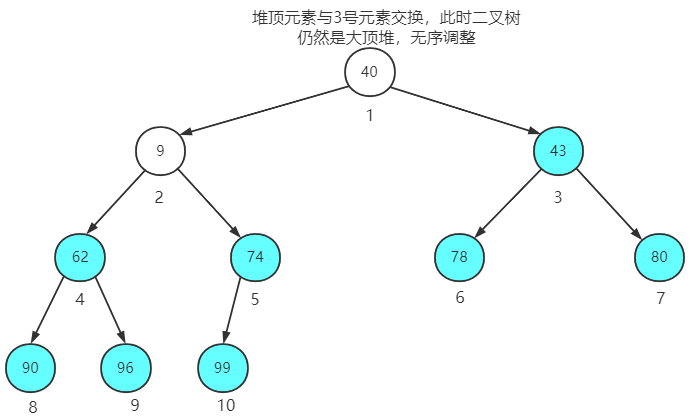
堆顶元素与第2个元素交换位置，也同样无需再调整成堆

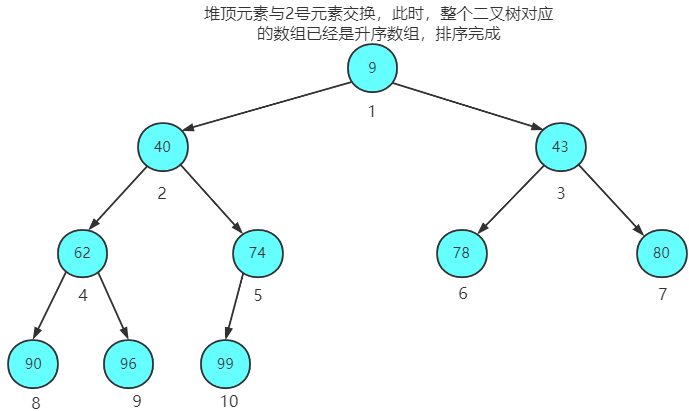
结束

6.3 代码

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define swap(a, b) {
    __typeof(a) __temp = a;
    a = b;
    b = __temp;
}

void down_update(int *arr, int n, int index) {
    while ((index << 1) <= n) {
        int temp = index, l = index << 1, r = index << 1 | 1;
        if (arr[l] > arr[temp]) temp = l;
        if (r <= n && arr[r] > arr[temp]) temp = r;
        if (index == temp) break;
        swap(arr[temp], arr[index]);
        index = temp;
    }
    return ;
}

void heap_sort(int *arr, int n) {
    arr -= 1;
    for (int i = n >> 1; i >= 1; i--) {
        down_update(arr, n, i);
    }
    for (int i = n; i > 1; i--) {
        swap(arr[i], arr[1]);
        down_update(arr, i - 1, 1);
    }
    return ;
}

void output(int *arr, int n) {
    printf("[");
    for (int i = 0; i < n; i++) {
        i && printf(" ");
        printf("%-2d", arr[i]);
    }
    printf("]
");
}

int main(void) {
    srand(time(0));
    #define max_n 20
    int *arr = (int *)malloc(sizeof(int) * max_n) ;
    for (int i = 0; i < max_n; i++) {
        arr[i] = rand() % 100;
    }
    output(arr, max_n);
    heap_sort(arr, max_n);
    output(arr, max_n);
    free(arr);
    #undef max_n
    return 0;
}

未完待续。。。