DP凸优化
题目并不难
先转化问题,显然k=0的时候我们都知道是求直径,然后k=1就是选两条点不相交的链拼起来,很容易推出题目就是要我们在树上选$k+1$条点不相交的链
事实上你直接按照边不相交做,取k+1次直径都可以得到50pts的好成绩,我佛了(不要问我怎么知道的
这个东西是可以DP的(稍微有点麻烦):设$dp[i][j][0/1/2]$表示以$i$为根的子树里选出j条链,这时i的度数为0/1/2的最优解。度数为零表示i是单独一个点,度数为1表示是链的端点,度数为2就是链中间的一个点
然后转移就是拼来拼去,看代码吧
60pts暴力DP↓

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=300005,K=105; 6 int n,k,t1,t2,t3,cnt; 7 long long dp[N][K][3]; 8 int p[N],noww[2*N],goal[2*N],val[2*N],siz[N]; 9 void Maxi(long long &x,long long y) 10 { 11 if(x<y) x=y; 12 } 13 void Link(int f,int t,int v) 14 { 15 noww[++cnt]=p[f],p[f]=cnt; 16 goal[cnt]=t,val[cnt]=v; 17 noww[++cnt]=p[t],p[t]=cnt; 18 goal[cnt]=f,val[cnt]=v; 19 } 20 void DFS(int nde,int fth) 21 { 22 siz[nde]=1; 23 dp[nde][0][0]=dp[nde][1][1]=dp[nde][1][2]=0; 24 for(int i=p[nde];i;i=noww[i]) 25 if(goal[i]!=fth) 26 { 27 int g=goal[i]; DFS(g,nde); 28 for(int j=min(siz[nde],k);~j;j--) 29 for(int h=min(siz[goal[i]],k-j+1);~h;h--) 30 { 31 for(int l=0;l<=2;l++) 32 for(int f=0;f<=2;f++) 33 Maxi(dp[nde][j+h][l],dp[nde][j][l]+dp[g][h][f]); 34 if(j+h<k) Maxi(dp[nde][j+h+1][1],dp[nde][j][0]+dp[g][h][0]+val[i]); 35 Maxi(dp[nde][j+h][1],dp[nde][j][0]+dp[g][h][1]+val[i]); 36 Maxi(dp[nde][j+h][2],dp[nde][j][1]+dp[g][h][0]+val[i]); 37 if(j&&h) Maxi(dp[nde][j+h-1][2],dp[nde][j][1]+dp[g][h][1]+val[i]); 38 } 39 siz[nde]+=siz[goal[i]]; 40 } 41 } 42 int main() 43 { 44 scanf("%d%d",&n,&k),k++; 45 for(int i=1;i<n;i++) 46 { 47 scanf("%d%d%d",&t1,&t2,&t3); 48 Link(t1,t2,t3); 49 } 50 memset(dp,0xc0,sizeof dp),DFS(1,0); 51 printf("%lld",max(dp[1][k][0],max(dp[1][k][1],dp[1][k][2]))); 52 return 0; 53 }
考虑优化
官方的题解是这么写的:
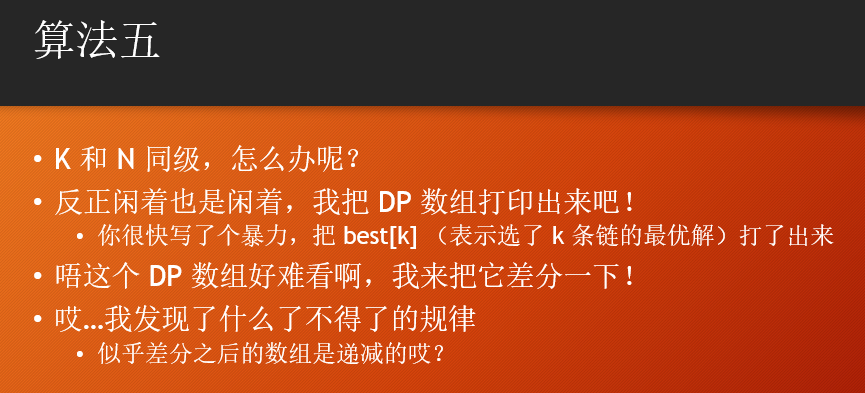
好吧我们不管具体过程,先假装我们发现了这个规律。
差分后递减,说明这是个上凸函数(以选取的链数为x轴,最优解为y轴)。这种DP有个套路的优化方法叫做凸优化:二分斜率,然后我们强制选取物品时额外付出斜率的代价(这里是选链)。这时套用原来那个DP(把它当成一个黑箱,输入直线输出切点),相当于不限制数目地选取。最后得到一个最优情况下选出来的数目,根据这个数目调整二分上下界即可。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=600005; 6 int p[N],noww[N],goal[N],val[N]; 7 int n,k,t1,t2,t3,cnt; long long del; 8 struct a 9 { 10 int cho; 11 long long sum; 12 }dp[N][3]; 13 a operator + (a x,a y) 14 { 15 return (a){x.cho+y.cho,x.sum+y.sum}; 16 } 17 bool operator < (a x,a y) 18 { 19 if(x.sum^y.sum) return x.sum<y.sum; 20 return x.cho<y.cho; 21 } 22 void Maxi(a &x,a y) 23 { 24 if(x<y) x=y; 25 } 26 void Link(int f,int t,int v) 27 { 28 noww[++cnt]=p[f],p[f]=cnt; 29 goal[cnt]=t,val[cnt]=v; 30 noww[++cnt]=p[t],p[t]=cnt; 31 goal[cnt]=f,val[cnt]=v; 32 } 33 void DFS(int nde,int fth) 34 { 35 dp[nde][2]={1,-del}; 36 for(int i=p[nde];i;i=noww[i]) 37 if(goal[i]!=fth) 38 { 39 int g=goal[i]; DFS(g,nde); 40 dp[nde][2]=max(dp[nde][2]+dp[g][0],dp[nde][1]+dp[g][1]+(a){1,val[i]-del}); 41 dp[nde][1]=max(dp[nde][1]+dp[g][0],dp[nde][0]+dp[g][1]+(a){0,val[i]}); 42 dp[nde][0]=dp[nde][0]+dp[g][0]; 43 } 44 Maxi(dp[nde][0],dp[nde][1]+(a){1,-del}); 45 Maxi(dp[nde][0],dp[nde][2]); 46 } 47 int Calc(long long x) 48 { 49 del=x; 50 for(int i=1;i<=n;i++) 51 dp[i][0]=dp[i][1]=(a){0,0}; DFS(1,0); 52 return dp[1][0].cho; 53 } 54 int main() 55 { 56 scanf("%d%d",&n,&k),k++; 57 for(int i=1;i<n;i++) 58 { 59 scanf("%d%d%d",&t1,&t2,&t3); 60 Link(t1,t2,t3); 61 } 62 long long l=-1e12,r=1e12,ans=0; 63 while(l<=r) 64 { 65 long long mid=(l+r)>>1; 66 (Calc(mid)>=k)?l=mid+1,ans=mid:r=mid-1; 67 } 68 Calc(ans),printf("%lld",dp[1][0].sum+ans*k); 69 return 0; 70 }
