
一看到这个题
就感觉。。。cao,,
什么东西。。。??!
然后就开始暴力求Fn
然鹅我并不会写高精(我太菜了)
只能求到大概10左右
在吧Fn给质因数分解
求出其因子个数
妄图找到什么有关的规律
但是我太过于弱小
并未找到。。。。。。。
(yjg:你找不到规律,并不代表没有规律)
然而我还瞎jb乱模
导致局面甚是混乱
但是,,,,
质因数分解貌似有点苗头,,,
而且这个东西
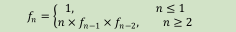
像极了斐波那契数列
那如果是两相结合
就是正解!!!
我的40分代码:
可能是写的太过繁琐
导致TLE

#include<cstdio> #include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int mod=1e9+7; int f[4][5000005]; int n; int main() { freopen("fiborial.in","r",stdin); freopen("fiborial.out","w",stdout); cin>>n; for(int i=2; i<=n; i++) { int k=i,t=2; for(int j=2; j<=i; j++) f[3][j]=f[1][j]+f[2][j],f[3][j]%=mod; while(k>1) { while(k%t==0) { k/=t; f[3][t]++; } t++; } for(int j=2; j<=i; j++) { f[1][j]=f[2][j]; f[2][j]=f[3][j]; } } long long ans=1; for(int i=2; i<=n; i++) ans*=(f[3][i]+1),ans%=mod; cout<<ans; fclose stdin; fclose stdout; return 0; }
那么就让我们看看
牛逼哄哄的土蛋的代码吧
上!

#include <cstdio> #include <cstdlib> typedef long long ll; const int N = (int)5e6; const int S = (int)1e6; const int mod = (int)1e9 + 7; int f[N + 1], n, p[S + 1], cnt = 0, m[N + 1], c[N + 1]; bool v[N + 1]; inline int add(int a, int b) { int r = a + b; return r >= mod ? r - mod : r; } int main() { freopen("fiborial.in", "r", stdin); freopen("fiborial.out", "w", stdout); scanf("%d", &n); f[0] = f[1] = 1; for (int i = 2; i <= n; ++i) f[i] = add(f[i - 1], f[i - 2]); for (int i = 2; i <= n; ++i) { if (!v[i]) p[cnt++] = i, m[i] = i; for (int j = 0, tmp; j < cnt && (tmp = i * p[j]) <= n; ++j) { v[tmp] = true, m[tmp] = p[j]; if (!(i % p[j])) break; } } for (int i = 2; i <= n; ++i) for (int x = i; x != 1; x /= m[x]) c[m[x]] = add(c[m[x]], f[n - i]); int ans = 1; for (int i = 0; i < cnt; ++i) ans = (ll)ans * (c[p[i]] + 1) % mod; printf("%d ", ans); return 0; }

