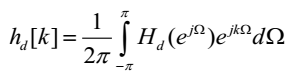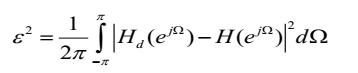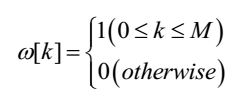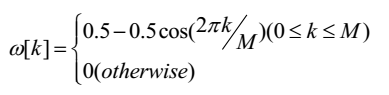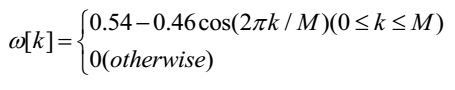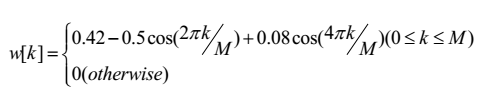1.前言
在数字信号处理中 ,由于信号中经常混有各种复杂成分,所以很多信号分析都是基于滤波器而进行的, 因此数字滤波器占有极其重要的地位 。数字滤波器是具有一定传输选择特性的数字信号处理装置,其输入与输出均为数字信号,实质上是一个由有限精度算法实现的线性时不变离散系统。它的基本工作原理是利用离散系统特性对系统输入信号进行加工和变换,改变输入序列的频谱或信号波形,让有用频率的信号分量通过,抑制无用的信号分量输出。数字滤波器和模拟滤波器有着相同的滤波概念,根据其频率响应特性可分为低通、高通、带通、带阻等类型。与模拟滤波器相比,数字滤波器除了具有数字信号处理固有优点外,还有滤波精度高、稳定性好、灵活性强等优点。 FIR 滤波器可以得到严格的线性相位,但它的传递函数的极点固定在原点,只能通过改变零点位置来改变性能,为了达到高的选择性,必须用较高的阶数,对于同样的滤波器设计指标,FIR 滤波器要求的阶数可能比 IIR 滤波器高 5~10 倍。
由于 FIR 数字滤波器具有严格的相位特性,对于信号处理和数据传输是很重要的。目前 FIR 滤波器的设计方法主要有三种:窗函数法、频率抽样法和优化设计(切比雪夫逼近)方法。
2.窗函数法设计 FIR 滤波器思想
窗函数设计法又称为傅里叶级数法。这种方法首先给出 H(jΩ), H(jΩ) 表示要逼近的理想滤波器的频率响应,则由 IDTFT 可得出滤波器的单位脉冲响应为:
由于是理想滤波器,故 hd[k]是无限长序列。但是我们所要设计的 FIR 滤波器,其 h[k]是有限长的。为了能用 FIR 滤波器近似理想滤波器,需将理想滤波器的无限长单位脉冲响应 hd[k]分别从左右进行截断。当截断后的单位脉冲响应hd[k]不是因果系统的时候,可将其右移从而获得因果的 FIR 滤波器。
(核心:理想滤波器频率设计->反变换时域无限长信号->信号截断->右移变因果系统)
理想滤波器的频率响应 Hd()和设计出的滤波器的频率响应 Hd()的积分平方误差定义为:
3.吉布斯现象产生的原因
Gibbs 现象就是理想滤波器的单位脉冲响应hd[k]截断获得的 FIR 滤波器的幅度函数 A(Ω) 在通带和阻带都呈现出振荡现象。随着滤波器阶数的增加,幅度函数在通带和阻带振荡的波纹数量也随之增加,波纹的宽度随之减小,然而通带和阻带最大波纹的幅度与滤波器的阶数 M 无关。窗函数的主瓣宽度决定了Hd (jΩ)过渡带的宽度,窗函数长度 N 增大,过渡带减小。
下面介绍一些常用的窗函数,用 N=M+1 表示窗函数的长度。
3.1 矩形窗 Rectangle
特点:矩形窗使用最多,习惯上不加窗就是使信号通过了矩形窗。这种窗的优点是主瓣比较集中,缺点是旁瓣较高,并有负旁瓣,导致变换中带进了高频干扰和泄漏,甚至出现负谱现象。频率识别精度最高,幅值识别精度最低,所以矩形窗不是一个理想的窗。
应用:如果仅要求精确读出主瓣频率,而不考虑幅值精度,则可选用矩形窗,例如测量物体的自振频率等,也可以用在阶次分析中。
3.2 汉宁窗 Hanning
特点:主瓣加宽并降低,旁瓣则显著减小,从减小泄漏观点出发,汉宁窗优于矩形窗。但汉宁窗主瓣加宽,相当于分析带宽加宽,频率分辨力下降。它与矩形窗相比,泄漏、波动都减小了,并且选择性也提高。应用:汉宁窗是很有用的窗函数。如果测试信号有多个频率分量,频谱表现的十分复杂,且测试的目的更多关注频率点而非能量的大小,需要选择汉宁窗。如果被测信号是随机或者未知的,选择汉宁窗。3.3 海明窗 Hamming
特点:与汉宁窗都是余弦窗,又称改进的升余弦窗,只是加权系数不同,使旁瓣达到更小。但其旁瓣衰减速度比汉宁窗衰减速度慢。应用:与汉明窗类似,也是很有用的窗函数。3.4 高斯窗 Gaussian
特点:是一种指数窗。主瓣较宽,故而频率分辨力低;无负的旁瓣,第一旁瓣衰减达一55dB。常被用来截短一些非周期信号,如指数衰减信号等。应用:对于随时间按指数衰减的函数,可采用指数窗来提高信噪比。3.5布莱克曼窗 Blackman
特点:二阶升余弦窗,主瓣宽,旁瓣比较低,但等效噪声带宽比汉宁窗要大一点,波动却小一点。频率识别精度最低,但幅值识别精度最高,有更好的选择性。应用:常用来检测两个频率相近幅度不同的信号。3.6 平顶窗 Flap Top
特点:平顶窗在频域时的表现就象它的名称一样有非常小的通带波动。应用:由于在幅度上有较小的误差,所以这个窗可以用在校准上。
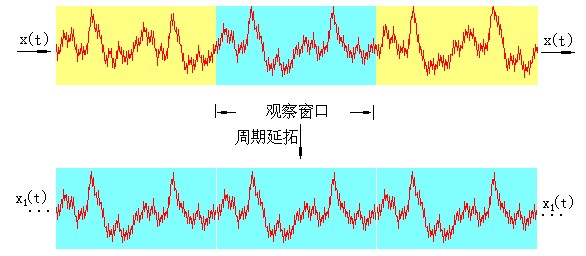
4.信号的截断及能量泄漏效应
数字信号处理的主要数学工具是傅里叶变换。应注意到,傅里叶变换是研究整个时间域和频率域的关系。然而,当运用计算机实现工程测试信号处理时,不可能对无限长的信号进行测量和运算,而是取其有限的时间片段进行分析。做法是从信号中截取一个时间片段,然后用观察的信号时间片段进行周期延拓处理,得到虚拟的无限长的信号,然后就可以对信号进行傅里叶变换、相关分析等数学处理。信号截断以后产生的能量泄漏现象是必然的,因为窗函数w(t)是一个频带无限的函数,所以即使原信号x(t)是限带宽信号,而在截断以后也必然成为无限带宽的函数,即信号在频域的能量与分布被扩展了.又从采样定理可知,无论采样频率多高,只要信号一经截断,就不可避免地引起混叠,因此信号截断必然导致一些误差,这是信号分析中不容忽视的问题.如果增大截断长度T,即矩形窗口加宽,则窗谱 W(ω)将被压缩变窄(π/T减小).虽然理论上讲,其频谱范围仍为无限宽,但实际上中心频率以外的频率分量衰减较快,因而泄漏误差将减小.当窗口宽度T趋于无穷大时,则谱窗W(ω)将变为δ(ω)函数,而δ(ω)与X(ω)的卷积仍为X(ω),这说明,如果窗口无限宽,即不截断,就不存在泄漏误差。为了减少频谱能量泄漏,可采用不同的截取函数对信号进行截断,截断函数称为窗函数,简称为窗。泄漏与窗函数频谱的两侧旁瓣有关,如果两侧瓣的高度趋于零,而使能量相对集中在主瓣,就可以较为接近于真实的频谱,为此,在时间域中可采用不同的窗函数来截断信号。