Lucene单词词典
使用lucene进行查询不可避免都会使用到其提供的单词词典功能,即根据给定的term找到该term所对应的倒排文档id列表等信息。实际上lucene索引文件后缀名为tim和tip的文件实现的就是lucene的单词词典功能。
怎么实现一个单词词典呢?我们马上想到排序数组,即term字典是一个已经按字母顺序排序好的数组,数组每一项存放着term和对应的倒排文档id列表。每次载入索引的时候只要将term数组载入内存,通过二分查找即可。这种方法查询时间复杂度为Log(N),N指的是term数目,占用的空间大小是O(N*str(term))。排序数组的缺点是消耗内存,即需要完整存储每一个term,当term数目多达上千万时,占用的内存将不可接受。
单词词典是倒排索引中非常重要的组成部分,它用来维护文档集合中出现过的所有单词的相关信息,同时用来记载某个单词对应的倒排列表在倒排文件中的位置信息,如图1-2所示。在支持搜索时,根据用户的查询词,去单词词典里查询,就能够获得相应的倒排列表,并以此作为后续排序的基础。
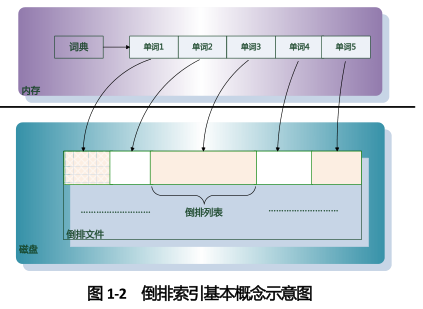
对于一个规模很大的文档集合来说,可能包含几十万甚至上百万的不同单词,能否快速定位某个单词,这直接影响搜索时的响应速度,所以需要高效的数据结构来对单词词典进行构建 和查找,常用的数据结构包括哈希加链表结构和树形词典结构和FST有穷状态转换器。
很多数据结构均能完成字典功能,总结如下。
| 数据结构 | 优缺点 |
| 排序列表Array/List | 使用二分法查找,不平衡 |
| HashMap/TreeMap | 性能高,内存消耗大,几乎是原始数据的三倍 |
| Skip List | 跳跃表,可快速查找词语,在lucene、redis、Hbase等均有实现。相对于TreeMap等结构,特别适合高并发场景(Skip List介绍) |
| Trie | 适合英文词典,如果系统中存在大量字符串且这些字符串基本没有公共前缀,则相应的trie树将非常消耗内存(数据结构之trie树) |
| Double Array Trie | 适合做中文词典,内存占用小,很多分词工具均采用此种算法(深入双数组Trie) |
| Ternary Search Tree | 三叉树,每一个node有3个节点,兼具省空间和查询快的优点(Ternary Search Tree) |
| Finite State Transducers (FST) | 一种有限状态转移机,Lucene 4有开源实现,并大量使用 |
一:哈希加链表
图 1-3 是这种词典结构的示意图。这种词典结构主要由两个部分构成,主体部分是哈希表, 每个哈希表项保存一个指针,指针指向冲突链表,在冲突链表里,相同哈希值的单词形成链表结构。之所以会有冲突链表,是因为两个不同单词获得相同的哈希值,如果是这样,在哈希方法里被称做是一次冲突,可以将相同哈希值的单词存储在链表里,以供后续查找。
注:
-》主体部分为什么使用哈希表?
数组、向量、集合等都可以存储对象,但是对象的位置是随机的,也就是说对象本身和位置并没有必然的联系,当要查找一个对象时,只能以某种顺序(如顺序查找或二分查找)与各个元素进行比较,当数组或向量或集合中的元素数量很多时,查找的效率会明显的降低。Hash表利用key、value模式,散列无序存储,效率高很多。
-》为什么会有Hash冲突?
哈希的原理就是抽样,取信息的特征。两个不同单词通过hash算法获得哈希值是有可能相同的(如果是这样,在哈希方法里被称做是一次冲突),而实际的哈希表,全部都要处理哈希值冲突的情况。而链表法就是解决hash冲突的一种手段(可以将相同哈希值的单词存储在链表里,以供后续查找),如:向哈希表中添加一个词汇2时,如果哈希表中已经存在一个具有相同哈希值的词汇1,则将词汇2添加到以词汇1为头节点的链表中。
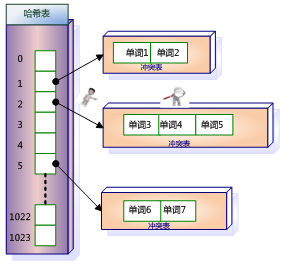
图1-3 哈希加冲突链表词典结构
在建立索引的过程中,词典结构也会相应地被构建出来。比如在解析一个新文档的时候,对于某个在文档中出现的词汇A:
第1步:首先利用哈希函数获得其哈希值
第2步:之后根据哈希值对应的哈希表项读取其中保存的指针,找到了对应的冲突链表。
第3步:如果冲突链表里已经存在这个单词, 说明单词在之前解析的文档里已经出现过。
第4步:如果在冲突链表里没有发现这个单词,说明该单词是首次碰到,则将其加入冲突链表里。
通过这种方式,当文档集合内所有文档解析完毕时,相应的词典结构也就建立起来了。
在响应用户查询请求时,其过程与建立词典类似,不同点在于即使词典里没出现过某个单词, 也不会添加到词典内。以图 1-3 为例,
第1步:假设用户输入的查询请求为单词3,对这个单词进行哈希。
第2步:定位到哈希表内的 2 号槽。
第3步:从其保留的指针可以获得冲突链表。
第4步:依次将单词 3 和冲突链表内的单词比较,发现单词 3 在冲突链表内,于是找到这个单词。之后可以读出这个单词对应的倒排列表来进行后续的工作。
第5步:如果没有找到这个单词,说明文档集合内没有任何文档包含单词,则搜索结果为空。
二:树形结构
B 树(或者 B+树)是另外一种高效查找结构,图 1-4 是一个 B 树结构示意图。B树与哈希方式查找不同,需要字典项能够按照大小排序(数字或者字符序),而哈希方式则无须数据满足此项要求。
B 树形成了层级查找结构,中间节点用于指出一定顺序范围的词典项目存储在哪个子树中, 起到根据词典项比较大小进行导航的作用,最底层的叶子节点存储单词的地址信息,根据这个地址就可以提取出单词字符串。
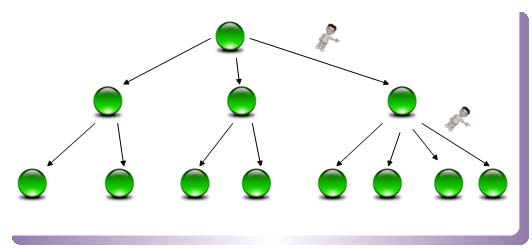
图1-4 B树查找结构
三:FST有穷状态转换器
Finite State Transducers 简称 FST, 中文名:有穷状态转换器。在自然语言处理等领域有很大应用,其功能类似于字典的功能(STL 中的map,C# 中的Dictionary),但其查找是O(1)的,仅仅等于所查找的key长度。目前Lucene4.0在查找Term时就用到了该算法来确定此Term在字典中的位置。
lucene从4开始大量使用的数据结构是FST(Finite State Transducer)。FST有两个优点:1)空间占用小。通过对词典中单词前缀和后缀的重复利用,压缩了存储空间;2)查询速度快。O(len(str))的查询时间复杂度。
下面简单描述下FST的构造过程。我们对“cat”、 “deep”、 “do”、 “dog” 、“dogs”这5个单词进行插入构建FST(注:必须已排序)。
1)插入“cat”
插入cat,每个字母形成一条边,其中t边指向终点。

2)插入“deep”
与前一个单词“cat”进行最大前缀匹配,发现没有匹配则直接插入,P边指向终点。

3)插入“do”
与前一个单词“deep”进行最大前缀匹配,发现是d,则在d边后增加新边o,o边指向终点。

4)插入“dog”
与前一个单词“do”进行最大前缀匹配,发现是do,则在o边后增加新边g,g边指向终点。

5)插入“dogs”
与前一个单词“dog”进行最大前缀匹配,发现是dog,则在g后增加新边s,s边指向终点。

最终我们得到了如上一个有向无环图。利用该结构可以很方便的进行查询,如给定一个term “dog”,我们可以通过上述结构很方便的查询存不存在,甚至我们在构建过程中可以将单词与某一数字、单词进行关联,从而实现key-value的映射。
FST压缩率一般在3倍~20倍之间,相对于TreeMap/HashMap的膨胀3倍,内存节省就有9倍到60倍!那FST在性能方面真的能满足要求吗?
下面是我在苹果笔记本(i7处理器)进行的简单测试,性能虽不如TreeMap和HashMap,但也算良好,能够满足大部分应用的需求。

参考博文:
sbp810050504 《lucene (42)源代码学习之FST(Finite State Transducer)在SynonymFilter中的实现思想》
zhanlijun 《lucene字典实现原理》