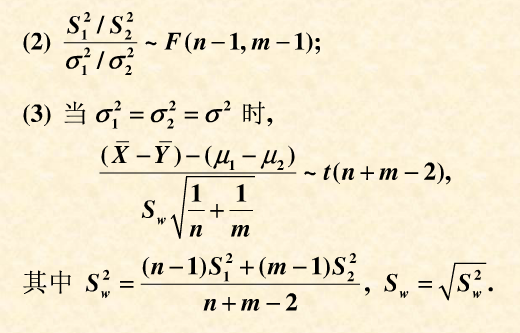概率论中,所研究的随机变量是假定其分布是已知的,在此前提下研究它的性质、数字特征等。
在数理统计中,所研究的随机变量的分布是未知或不完全知道的,通过重复独立的试验得到许多观察值去推断随机变量的种种可能分布。
1、随机样本
总体:试验的全部可能的观察值。 =样本空间
个体:每一个可能观察值。 =样本点
容量:总体中所包含的个体的个数。
有限总体
无限总体
一个总体对应一个随机变量X,对总体的研究就是对随机变量X的研究。所以将不区分总体与相应的随机变量,统称为总体X。
样本:在数理统计中,人们都是通过从总体中抽取一部分个体,根据获得的数据来对总体分布得出推断的,被抽出的部分个体叫做总体的一个样本。
对总体进行一次观察,就会得到一个随机变量X1,对总体进行n次重复的、独立的观察,就会得到n个随机变量X1,X2,...,Xn,这n个随机变量X1,X2,...,Xn是对总体随机变量X观察的结果。则X1,X2,...,Xn是相关独立且与X具有相同分布,称为来自总体X的一个简单随机样本。n称为样本的容量。进行n次观察得到的一组实数x1,x2,...,xn是随机变量X1,X2,...,Xn的观察值,称为样本值,也称为X的n个独立的观测值。
2、抽样分布
样本是统计推断的依据,但往往不直接使用样本本身,而是由样本构造的函数。
统计量:设X1,X2,...,Xn是来自总体X的一个样本,g(X1,X2,...,Xn)是其函数,且g中不含任何未知参数,则称g(X1,X2,...,Xn)是一统计量。统计量也是一个随机变量。
g(x1,x2,...,xn)是统计量的观测值。
常用的统计量:

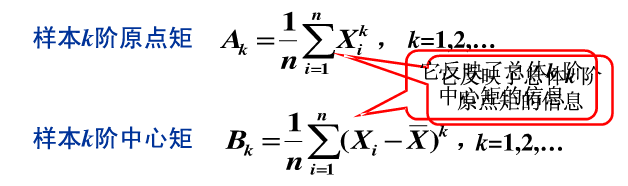
经验分布函数:
经验分布函数(empirical distribution function)是根据样本得到的分布函数.如设 ![]() ,是总体的样本值,将它们按大小顺序排列为
,是总体的样本值,将它们按大小顺序排列为![]() ,则称分布函数为
,则称分布函数为 ![]()

经验分布函数是与总体分布函数相对应的统计量。
总体的分布函数是F(x),统计量的经验分布函数是Fn(x),用Fn(x)去推断F(x),当n足够大时,Fn(x)以概率1收敛于F(x)。
统计量的分布称为抽样分布。
以下介绍的是来自正态总体的几个常用统计量的分布:
卡方分布:
设X1,X2,...,Xn来自总体N(0,1)的样本,则称统计量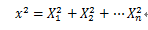 服从自由度为n的卡方分布。记为Χ2~Χ2(n)
服从自由度为n的卡方分布。记为Χ2~Χ2(n)
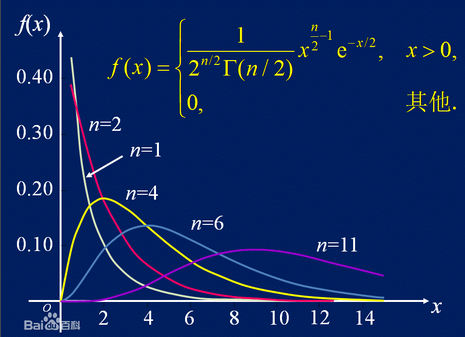

卡方分布的上ª分位点:
t分布
设X~N(0,1),Y~X2(n),且X,Y独立,则称随机变量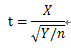 服从自由度为n的t分布。记为t~t(n).
服从自由度为n的t分布。记为t~t(n).
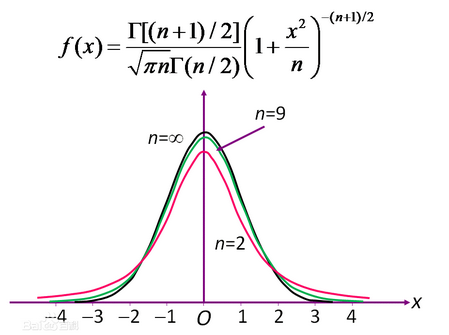
特征:
 服从自由度(n1,n2)的F分布。记为F~F(n1,n2).
服从自由度(n1,n2)的F分布。记为F~F(n1,n2).
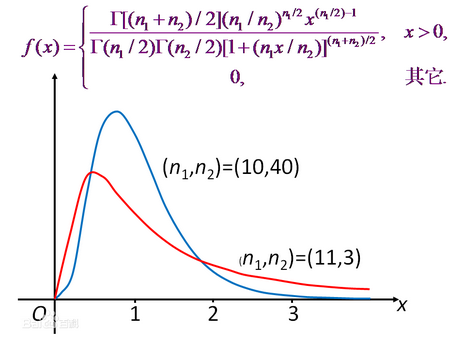

F分布的上ª分位点: