1、大数定律
背景:随着试验次数的增加,事件发生的频率逐渐稳定于一个值;算数平均值逐渐稳定于数学期望。
契比雪夫定理
贝努利大数定理
辛钦定理
结论:随机变量X1,X2,....Xn,...相互独立,且具有相同的数学期望和方差,当n趋于无穷大时,频率趋于概率,算数平均值趋于数学期望。
2、中心极限定理
独立同分布的中心极限定理
李雅普诺夫定理
利莫佛拉普拉斯定理
结论:1、正态分布是二项分布的极限分布。
2、无论各个随机变量服从什么分布,只要随机变量X1,X2,....Xn,...相互独立,当n趋于无穷大时,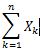 近似的服从正态分布。
近似的服从正态分布。